渗透压的依数性讨论*

卢雁 卢泽陈得军

(1河南师范大学化学与环境科学学院 河南新乡453007;2河南省医药学校 河南开封475001)

依数性是对少量非挥发性溶质与溶剂构成的稀溶液或理想溶液与纯溶剂相比，其沸点升高、凝固点降低、蒸气压下降及产生渗透压等性质而言。这些性质只取决于所含溶质分子的数目，与分子的本性无关。其中沸点升高、凝固点降低和蒸气压下降是指溶液的相变点与纯溶剂的相变点的差值随溶质浓度的变化关系。由于纯溶剂本身就具有沸点、凝固点和蒸气压，因此它们的概念比较清晰并易于理解，可以通过分别测定纯溶剂和稀溶液的相变点而得到。但是通常认为纯溶剂本身不具有渗透压，因此溶液渗透压的概念就比较抽象，同时也不能单独测定溶液的渗透压，必须借助半透膜与纯溶剂结合在一起进行测定。这就使得所测得的渗透压与溶质的性质有很大关系，在一些情况下与溶质浓度的关系也表现得比较复杂，因此需要对渗透压进行较深入的讨论。

1 渗透压的定义

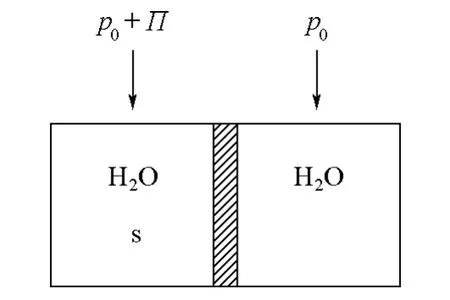
图1 渗透压示意图

产生渗透压的原因在于少量非挥发性溶质的溶入使溶液中溶剂的化学势低于纯溶剂的化学势。如图1所示，用半透膜把溶质s的稀溶液(左)和纯溶剂(右)隔开，半透膜只允许溶剂透过，而不允许溶质透过，这样由于化学势差别的推动作用，溶剂分子将从纯溶剂一侧渗透进入溶液一侧。为了阻止这一渗透行为，需要提高溶液中溶剂的化学势。溶液中溶剂的化学势与温度、压力和溶质的浓度有关，在温度和溶质浓度一定的情况下，则只是压力的函数。在溶液上方施加适当的额外压力可以把溶液中溶剂的化学势提高到与纯溶剂的化学势相等，从而阻止溶剂的渗透。这个适当的额外压力就称为溶液的渗透压，以Π表示。

如果我们将半透膜两侧分别放入不同浓度溶质s的稀溶液，半透膜两侧溶剂的化学势仍然是不相等的，因此溶剂分子仍将从更稀溶液一侧通过渗透进入到稍浓溶液一侧，这样仍然能够测出阻止此体系溶剂渗透的额外压力。半透膜两侧的溶液都具有各自的渗透压，而此时我们测出的额外压力实质是半透膜两侧液体的渗透压之差。如果我们将半透膜两侧都放入纯溶剂，则它们的化学势原本就相等，不施加额外的压力溶剂也不渗透，或者说施加零压力可以阻止溶剂的渗透。由此看来纯溶剂也有渗透压，只不过它的渗透压为0。因此不管半透膜右侧放的是溶液还是纯溶剂，通过类似图1的装置测出的阻止溶剂渗透的额外压力都可以看作是两侧液体的渗透压之差，只不过在一些情况下此额外压力与半透膜左侧溶液的渗透压相等，而在另一些情况下不相等。下边就不同情况进行讨论。

2 低浓度非电解质大分子溶液的渗透压

对非电解质大分子理想溶液(或稀溶液)的渗透压与溶质浓度的关系可以推导如下:令纯溶剂的化学势为，加入一定量的溶质，使溶剂的分数由1变为xA，再在溶液上方加上适当的额外压力Π，使压力由p变为p+Π，此时溶液中溶剂的化学势为［1］:

积分后得:

式中VA为溶液中溶剂的偏摩尔体积。如果施加的压力为该理想溶液的渗透压Πid，则该溶液中溶剂的化学势就等于纯溶剂的化学势。故上式可写为:

式中cB为溶质的浓度(mol/L)。此式被称作Van't Hoff渗透压公式。由此式可以看出:在恒温条件下溶液的渗透压与溶质的浓度有正比关系，即二者之间存在依数性。由于上式的约等号都仅对稀溶液适用，因此溶液的浓度越稀此式越适合。

严格地讲，实际溶液中溶剂的化学势应该与溶剂的活度aA有关，因此针对实际溶液式(1)应改写为:

积分后得:

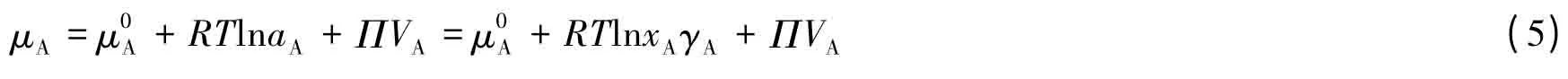
由于在一般的溶液中溶剂的活度系数γA与1相差很小，衡量溶剂在实际溶液和理想溶液的偏差不灵敏，溶液化学中常用渗透系数来代替［2］:

式中g为溶剂的合理渗透系数。将式(6)带入式(5)得:

同样，如果施加的压力为该实际溶液的渗透压Π，则该溶液中溶剂的化学势就等于纯溶剂的化学势。因此上式可写为:

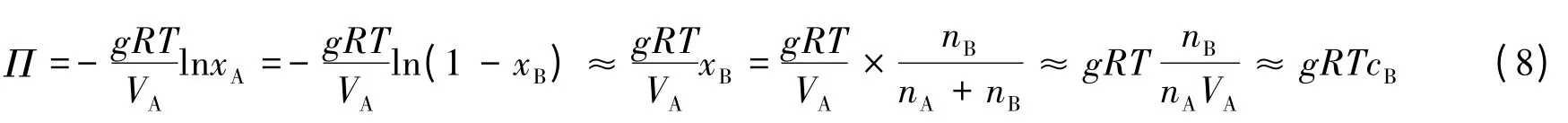
因为考虑了溶剂的渗透系数，上式对溶质浓度的适用范围较式(3)要大，但是由于式中仍有约等号，因此制约其不能用于溶质浓度过高的溶液。

将式(8)与式(3)相比可知g=Π/Πid，即渗透系数可看作相同条件下(溶剂、溶质的浓度、温度)实际稀溶液的渗透压与理想溶液的渗透压之比。只有当溶液足够稀，其渗透系数约等于1时，实际稀溶液的渗透压才能看作与理想溶液的渗透压相等。另外还有一种实用渗透系数Φ，它与溶剂活度的关系为［2］:

将式(9)代入式(5)，在施加的压力为该实际溶液的渗透压Π时得:

由式(8)和式(10)相比可以看出，合理渗透系数g和实用渗透系数Φ的定义式不同，但是当溶液很稀时，它们的数值是一样的。

3 较高浓度大分子溶液的渗透压

对于较高浓度大分子溶液必须考虑溶质间相互作用对渗透压的影响，此处仅简单介绍McMillan-Mayer的溶液理论［3］对渗透压的处理。根据此理论，溶液的渗透压可表示为:

式中ρ为溶质的质量浓度(g/L)，M为溶质的相对分子质量，B2、B3为第二、第三渗透维利系数，分别代表溶质间二分子相互作用和三分子相互作用对溶液渗透压的影响。当大分子溶质的浓度不是太高时，三分子及更多分子间的相互作用的影响可以忽略，式(11)可仅保留B2项。对于球形大分子，B2被联系到平均作用力势能W22(r):

其中NA为Avogadro常数，r表示两个分子间的中心距离。根据Prausnits等人提出的分子热力学模型，W22(r)可以采用4种势能加和的形式［4］:

其中Whs(r)为硬球势能，Welec(r)为静电排斥势能，Wdisp(r)为色散吸引势能，Wosmotic(r)为离子排斥体积产生的吸引势能。

4 纯聚电解质溶液的渗透压

在第二节中，利用非电解质大分子稀溶液得到溶液的渗透压与溶质之间具有依数性。实际上，不论溶质的性质如何，只要所有溶质及由溶质解离产生的粒子都透不过(或者不透过)半透膜，则其稀溶液的渗透压与溶质及由溶质产生的各种粒子的总和之间就具有依数性，这与沸点升高、凝固点降低及蒸气压下降的依数性是一样的。例如纯的聚电解质(如蛋白质、核酸等)在水溶液中会解离出小的离子，以蛋白质的钠盐为例，其解离方式为:

因此1摩尔纯的蛋白质钠盐在水溶液中会产生(z+1)摩尔的溶质粒子。如果半透膜另一侧为纯水，虽然从Na+的体积来看有透过半透膜的可能，但是它们却因为要保持电中性而与PZ-一起留在溶液一侧，并不透过半透膜。这样按照Van't Hoff公式，其渗透压的依数性关系为［5］:

5 有小分子存在时聚电解质溶液的渗透压

小分子可以透过半透膜，它的存在会使原来的纯溶剂成为小分子的稀溶液。同样，当由小离子构成的电解质存在时，它离解出的正、负离子也可以透过半透膜，使原来的纯溶剂成为电解质的稀溶液。如果没有与聚电解质相同的离子，则小离子的渗透和小分子的渗透都与聚电解质无关。它们的渗透一直到其在半透膜两侧的化学势相同(即达到膜平衡)为止，同时它们的浓度也达到相同。这时测出的阻止溶剂渗透的压力从定义上讲不是原来半透膜左侧溶液的渗透压，因为半透膜右侧已不是纯溶剂，而是另一种稀溶液。这两种稀溶液都有各自的渗透压，它们也都服从依数性原理。此时测出的压力是半透膜两侧溶液的渗透压之差，它是由半透膜两侧溶液中各种溶质的总浓度之差造成的。对于稀溶液，由于小分子或上述小离子在半透膜两侧的浓度相同，按照稀溶液的依数性原理，它们所产生的渗透压也相同，从而彼此抵消，所以此时测定的渗透压之差与纯聚电解质溶液的渗透压是相同的。

6与聚电解质具有同离子的电解质存在时聚电解质溶液的渗透压

如果小电解质与聚电解质具有同离子，则小电解质的渗透就会受到聚电解质大离子不能渗透的影响。同样当小电解质的渗透达到膜平衡时，半透膜两侧小电解质的化学势相同，但它们的离子浓度并不相同，因此就会对所测定的渗透压差产生影响，这种影响被称为唐南(Donnan)效应。

当测定的体系中存在与聚电解质具有同离子的小电解质时，无论小电解质是在半透膜的哪一侧，都会产生相同的唐南效应，这是因为它们总要渗透达到同样的膜平衡。图2和图3所示的两种情况均为体系中存在蛋白质的钠盐和氯化钠，所不同的是图2为渗透发生前NaCl存在于半透膜左侧，而图3为渗透发生前NaCl存在于半透膜右侧。图2所示体系的渗透压差可以根据唐南效应进行推导。

图2 渗透发生前NaCl存在于半透膜左侧示意图

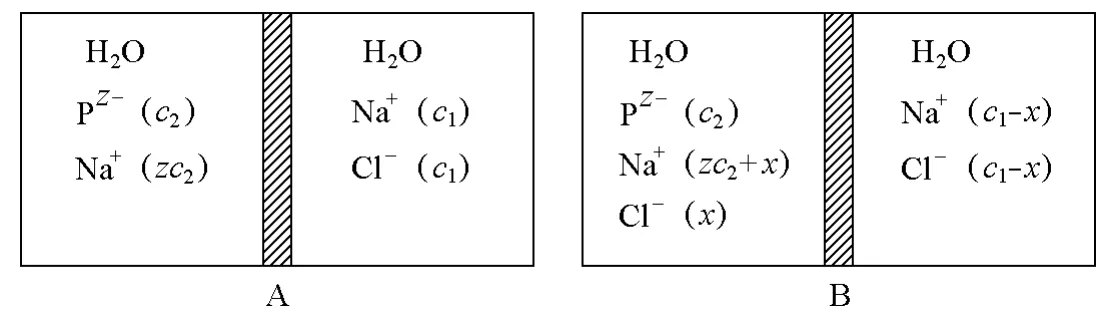
图3 渗透发生前NaCl存在于半透膜右侧示意图

当渗透达到平衡后，NaCl在膜两边的化学势相同，因此其活度相同。对于稀溶液，各种离子的活度系数均为1，活度可由浓度表示，故根据质量作用定律可得:

将图2(B)所示渗透平衡后的Na+和Cl-浓度代入上式，得:

解此方程得:

由于膜两边的渗透压差是由膜两边溶质粒子的总浓度差造成的，故:

将上式通分后可得:

图3所示的情况已在文献［5］中推导，其渗透压差与各离子浓度的关系同样为式(19)所表达［5］，推导过程不在此赘述。

由式(19)还可推得:

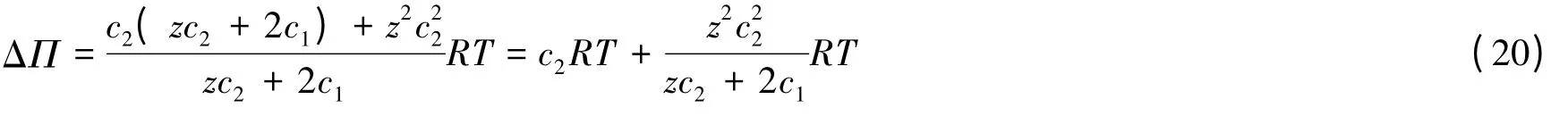
此式表明体系的渗透压差由两项组成，第1项是Van't Hoff效应的贡献，来自聚电解质本身;第2项是Donnan效应的贡献，来自于小电解质的膜平衡。对式(20)的分析还可得出:当c1远大于c2时，式(20)右端第2项可以忽略，这就相当于式(3)的结果。而当c1远小于c2时，可忽略式(20)右端第2项分母中的2c1，则右端成为(z+1)c2RT，这相当于式(14)的结果。

进一步还可将式(20)改写如下:

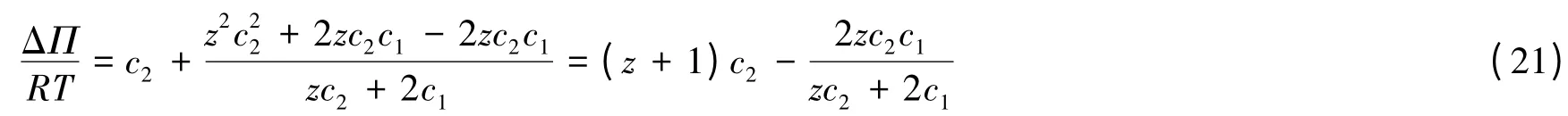
继续推导可得:

如果欲测定某一纯聚电解质溶液的浓度c2和聚电解质的电价z，可将此溶液注入渗透压计的溶液池，溶剂池依次注入纯水和一系列浓度的与聚电解质具有同离子的小电解质水溶液，分别测定它们的渗透压和渗透压差。由式(14)知:如果溶剂池中注入的是纯水，则测得的就等于(z+1)c2。由式(22)知:当(z+1)c2为已知时，等号左边与有直线关系，其斜率为截距为由此可作图，同时得到聚电解质溶液的浓度和聚电解质的电价。

7 渗透压测定的应用

依据渗透压的依数性，可以在不知道溶质相对分子质量的情况下，通过测定溶液的渗透压来确定溶液的浓度，进而根据溶质的总质量确定其相对分子质量。在Donnan效应建立之后，渗透压测定即被用来确定蛋白质的相对分子质量［6］，并经常被用于确定高聚物的相对分子质量。我国的科学工作者利用渗透压测定和黏度测定的方法，首先得到第二渗透维利系数，然后将其用于计算高聚物的相对分子质量［7-8］，这就考虑了溶液非理想性的影响，得到的相对分子质量更为准确。最近我们利用渗透压法建立了测定小粒径纳米粒子溶液浓度的方法，测定了合成出来的3nm粒径金粒子的浓度和质量［9］。

体液是生命机体的重要组成部分，可分为细胞内液和细胞外液，它们主要由水、无机盐和有机物组成，而细胞膜和毛细血管壁等具有半通透性，因此体液在机体内要达到渗透平衡。不管什么原因造成体液渗透压的紊乱，都会使人产生疾病，因此体液渗透压测定在医学中有许多的应用。例如:肾脏是调节体液的重要器官，尿液渗透压的测定是评价肾脏对体液浓缩和稀释功能的最适宜方法。血液对生命机体的重要作用不言而喻，血液渗透压是反映溶于血液中的全部溶质总含量及其变化的指标。如果血液渗透压发生紊乱就会出现高血渗综合征或低血渗综合征。在现代医学临床上，测定血液的渗透压对于诊断和治疗疾病提供了很有价值的依据［10］。

渗透压的测定还经常用于理论的研究和对理论的检验。例如:1980年Vilker等［11］测量了牛血清蛋白在0.15mol/L NaCl水溶液中，pH为4.5、5.4和7.4的3种情况下的渗透压，并用两种方法处理实验数据，一种方法是用经典的维利方程回归实验结果，得到第二、第三维利系数与牛血清蛋白净带电数的经验关联式;另一种方法是在统计力学的基础上，用修正硬球的椭圆模型，从理论上计算第二和第三维利系数，二者进行比较并对渗透压进行预测。1997年，Yousef等［12］测定了牛丙种球蛋白在pH为7.4，离子强度为0.13mol/L时的渗透压，并从最基本的渗透压的定义出发，提出了一个自由溶剂理论模型，根据膜两侧自由水分子在溶液中的分子比例来计算渗透压。我们也通过测定不同硫酸钠浓度和不同pH的牛血清蛋白水溶液的渗透压，在求得第二渗透维利系数后研究了牛血清蛋白分子间的静电排斥势能、色散吸引势能、离子排斥体积造成的吸引势能以及总势能与溶液pH及离子强度的依赖关系［13］。

［1］上海师范大学，河北师范大学，华中师范大学，等.物理化学(上册).第3版.北京:高等教育出版社，1991

［2］黄子卿.电解质溶液理论导论.修订版.北京:科学出版社，1983

［3］McMillan W G，Mayer J E.J Chem Phys，1945，13:276

［4］Moon Y U，Anderson C O，Blanch H W，et al.Fluid Phase Equilib，2000，168:229

［5］傅献彩，沈文霞，姚天扬，等.物理化学(下册).第5版.北京:高等教育出版社，2006

［6］Briggs D R.J Phys Chem，1935，39:983

［7］程熔时，阮梅娜，钱人元.化学学报，1958，24(3):217

［8］张俐娜，周光应，田黎.武汉大学学报，1981(3):45

［9］Lu Y，Wang L X，Chen D J，et al.Langmuir，2012，28:9282

［10］梁子钧，戴稼禾.体液渗透压测定在医学中的应用.北京:人民卫生出版社，1983

［11］Vilker V L，Colton C K，Smith K A.J ColloidⅠnterface Sci，1981，79(2):548

［12］Yousef M A，Datta R，Rodgers V G.J ColloidⅠnterface Sci，1998，197(1):108

［13］Lu Y，Chen D J，Wang G K，et al.J Chem Eng Data，2009，54:1975