水平隧道火灾临界风速的理论模型
徐志胜,赵红莉,李洪,姜学鹏,李冬
(中南大学 土木工程学院,湖南 长沙,410075)
水平隧道火灾临界风速的理论模型
徐志胜,赵红莉,李洪,姜学鹏,李冬
(中南大学 土木工程学院,湖南 长沙,410075)
从热物理学的角度,分析烟气不会发生逆流的临界条件,建立控制隧道火灾烟气蔓延的临界风速理论模型。并通过隧道列车火灾的缩尺寸模型试验和数值模拟计算对水平隧道火灾临界风速进行研究,确定理论模型中的待定系数。将理论预测值与Wu和Bakar模型的预测值进行对比研究。研究结果表明:由该模型计算得到的临界风速与试验测试值较吻合,验证了理论模型的可靠性;Wu和Bakar的模型对油池火灾临界风速的预测值偏低,本文所建立的理论模型不适合预测火源功率较高工况下的临界风速。
隧道火灾;临界风速;理论模型;缩尺寸试验;数值模拟
阻止火灾烟气逆着风流向上游方向蔓延的最小纵向通风速度称为临界风速。作为隧道通风系统设计最重要的指标之一,临界风速一直是国内外的一个重要研究课题。早在1976年,Heselden等[1−2]引入Froude数表征气流的运动状态,认为烟气逆流现象消失的临界Froude数为4.5,并结合试验数据推导出临界风速半经验公式,被广泛应用于各国公路、铁路、地铁隧道的防灾设计中,但该经验公式也存在其局限性。近年来,在火源功率[3−9]对临界风速的影响方面的研究取得了重大进步,结果表明当火源功率较低时,临界风速与其1/3 次方成正比;当火源功率增大到一定程度时,临界风速与其近似无关,同时也证明上述经验公式不适合预测火源功率较高工况下的临界风速。虽然有关临界风速的计算模型很多,但是,大多模型是基于 Froude数守恒并结合一些试验数据所得到的半经验公式,或是通过量纲分析、试验数据拟合得到的,并没有很好地揭示出火灾烟气不会发生逆流现象的原理。因此,本文作者从热物理学的角度出发,分析烟气不会发生逆流的临界条件,建立隧道临界风速的理论模型,并通过数值模拟确定理论模型中的待定系数,对所建立的理论模型进行验证并与前人的研究成果进行对比。
1 临界风速的理论预测
烟流在火焰热浮力和燃烧生成气体热动力的作用下,由火源表面沿垂直方向向隧道拱顶运动,如图 1所示。图1中:z为隧道高度方向的坐标;hm为火源表面至隧道拱顶的距离,m;u0为燃烧生成气体脱离火源表面的速度,m/s,umax为烟流微团的最大垂直速度,m/s。假设燃烧和风流运动状态是稳定的,烟流微团在运动过程中受到重力和浮力的作用,垂直运动过程中密度不变且无外界质量加入。
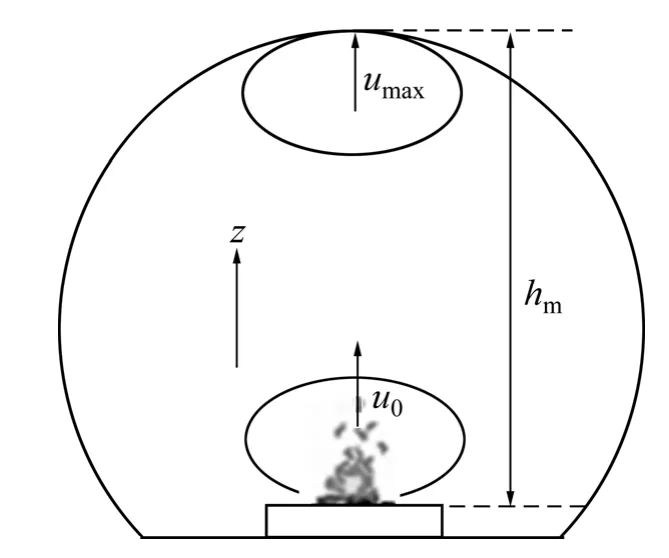
图1 烟流微团的运动Fig.1 Movement of smoke micro-groups
根据能量守恒定律可列方程式如下[10]:

燃烧生成气体离开火源表面的速度近似为0 m/s,即u0=0,由式(1)可以算出烟流微团的垂直速度:
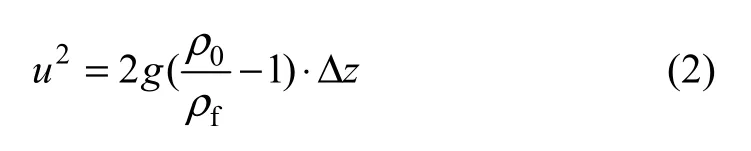
当烟流微团运动到拱顶附近时,垂直位移达最大值,烟流微团速度也达到最大值,有
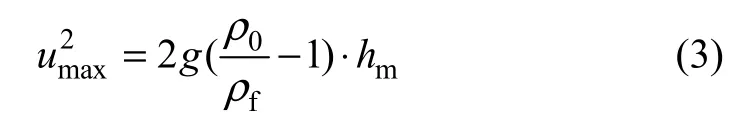
由烟气逆流层的形成过程可知:当烟流动能小于或等于隧道风流边界层风流动能时,烟气不会发生逆流[10]。因此,烟气不会发生逆流的临界条件为
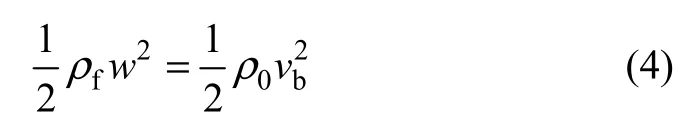
式中:vb为风流与隧道边界的边界层风速,与隧道临界风速uc成正比[11],即 b 1c v=ku;w为烟流在拱顶附近的逆流速度。垂直上升的烟流在隧道拱顶附近的动能转化为3部分:一部分在碰撞的同时,因烟流微团与隧道拱顶的摩擦,以及烟流微团间的内部摩擦而转化为热能,另外两部分转化为沿隧道向两侧运动的动能。若逆流速度与最大垂直速度成正比,即则代入式(4)得:

与通风气流的质量流量相比,可燃物燃烧生成的气体量可忽略不计。假定气流与隧道壁面之间没有热交换,则可以得出如下能量守衡式:

其中:m为风流的质量流量,kg/s;cp为比定压热容,kJ/(kg·K);T0为隧道着火前风流温度,K;Qc为火源功率中的对流部分,kw;Tf为烟流温度,K;A为隧道断面面积,m2。
由理想气体性质可得:

将式(6)和(7)代入式(5)整理得:

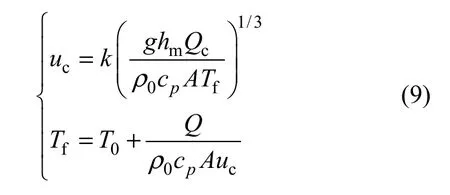
2 隧道火灾缩尺试验研究
2.1 试验设计
采用模型比例为1:9的缩尺模型试验来研究铁路隧道列车火灾的临界风速特性。在隧道列车火灾中,浮力效应起主导作用,火源附近的烟气流动为重力流,因此,模型试验采用Froude准则作为相似准则[12],试验数据可以根据一定的比例关系转换为实体条件下对应的同名参数值,重现实际隧道火灾场景,该比例关系如下:模型比例为Lm/Lp,速度比为(Lm/Lp)1/2,流量和火源功率为(Lm/Lp)5/2,温度为(Lm/Lp)0,下标m和p分别代表模型和实体隧道。
以广深港狮子洋水下铁路隧道为原型,模型隧道由21个分节组合拼装而成,采用钢板制造,每个分节长为2.5 m,截面内径为1.1 m,地面到拱顶的高度为96 cm,每节列车的长×宽×高为2.50 m×0.37 m×0.45 m。火源两边各放2节,为减小火源附近高温区的传热损失,在火源附近模型内部壁面张贴耐高温且导热和散热较差的石棉,以尽量接近混凝土的传热情况。采用油池火源方案对列车火灾的火源进行模拟,燃料采用甲醇(添加烟饼),在燃料盘下方放置称重天平测量燃料的质量随时间的变化关系,通过燃料的质量损失速率与燃料热值相乘获得火源功率。试验中采用了 3个不同尺寸的方形油盘,长×宽×高分别为0.33 m×0.30 m×0.08 m,0.45 m×0.30 m×0.08 m,0.61 m×0.30 m×0.08 m,分别用于模拟功率为42,63和85 kW的火源,对应全尺寸火源功率为10,15和20 MW;油盘放在模型中央处,距离地面0.2 m。各测点的布置如图2所示,在隧道拱顶中心线下方2 cm处沿纵向布置了51个K型热电偶,其中第1个和最后一个热电偶距离火源25 m,热电偶之间的间距为1 m,精度为0.5 ℃,共使用了6个温度数据采集模块,测量火源上下游50 m范围内的温度。实验中纵向风速由设在进风段的轴流风机提供,可采用调速电机对风量进行调节,试验前需进行风速标定。
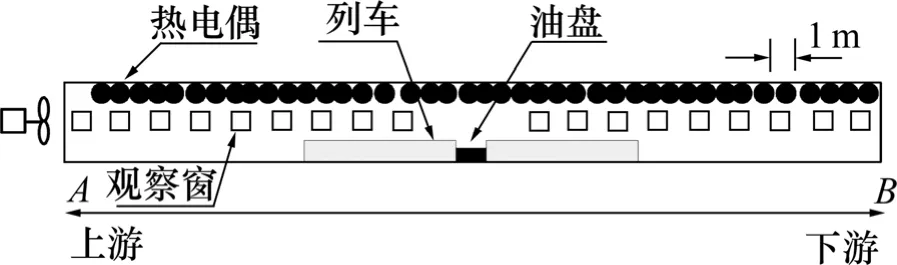
图2 模型隧道测点布置图Fig.2 Distribution of thermocouples in model tunnel
温度采集系统通过 RS-232总线以及 EWRF-302系列2UT型射频芯片来实现与智能传感器、上位PC机的无线通信,采集控制器定时与智能传感器通信以获得实时温度,上位机与采集控制器进行定时或随时通信可以得到各个传感器的最新采样值。
2.2 试验结果分析
试验结果给出了火源功率为15 MW时,不同纵向通风风速下拱顶温度的纵向分布,及其随通风风速的变化规律如图3所示。从图3可见:在纵向通风的作用下,高温烟气向火区下风侧方向移动,随着时间的延续,其影响的区域越来越大;同时,由于烟气的温度高于沿途衬砌的温度,因此,在扩散过程中,烟气不断地与周围物体进行热交换,隧道衬砌温度不断升高,烟流失去热能,温度逐渐下降,拱顶温度沿着纵向不断降低。同时,纵向通风对于抑制温度向火区上游的传播是相当有效的;当纵向风速为2 m/s时,高温气体影响了火源上游80 m范围内的区域,风速增大到3 m/s时,火源上游拱顶下方烟气温度均在环境温度附近。根据上游烟气温度随纵向风速的变化,可以初步判断火源功率为15 MW下抑制烟气回流的临界风速为 2~3 m/s。
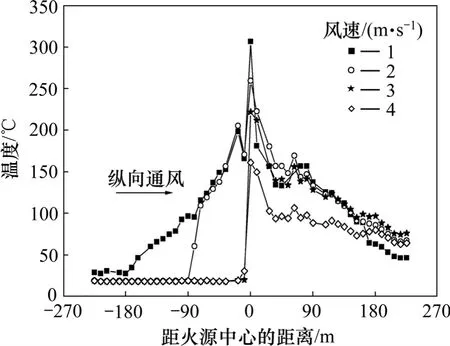
图3 不同纵向风速下拱顶下方温度分布Fig.3 Distributions of smoke temperature below tunnel ceiling under different ventilation velocities
在2~3 m/s风速范围内多次改变纵向风速,通过观察火源上游距火源中心1 m处的拱顶测点温度在不同通风风速下的变化趋势确定临界风速的范围,当该测点温度接近环境温度时,此时的通风风速即为临界风速。
根据模型隧道现场热烟试验的烟气蔓延观测结果和测点温度变化,各个油盘尺寸下的临界风速如表 1所示。

表1 各油盘火下的临界风速试验值Table 1 Critical wind velocities measured in fire tests with different pan sizes
3 隧道火灾的数值模拟
由于试验中考虑的火源功率有限,为了获得隧道火灾抑制烟气回流所需临界风速的更多信息,对隧道列车火灾进行数值模拟计算,并通过试验结果来验证数值模拟的可靠性。
3.1 数值模拟条件的设定
采用FDS软件,按照广深港狮子洋水下铁路隧道的相应尺寸建模进行数值模拟计算。计算域的尺寸为长600 m,宽9.8 m,高8.6 m,由于烟气的温度、浓度等参数主要在火源附近一段区域内具有重要变化[13−14],兼顾计算耗时经济性,火源附近的网格如图4所示,网格2位于火源前后50 m内,网格长×宽×高为0.30 m×0.27 m×0.27 m,其余的隧道部分采用网格1,其长×宽×高为1.00 m×0.27 m×0.27 m。
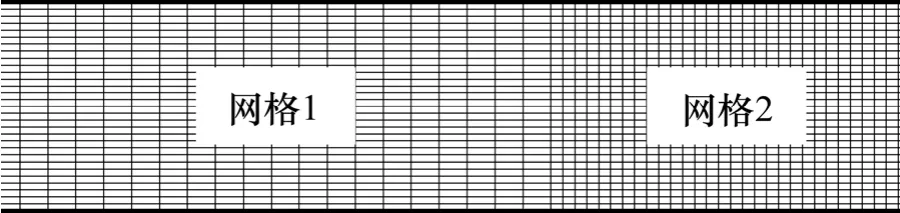
图4 数值模拟采用的2种网格尺寸Fig.4 Two grid sizes adopted in numerical simulation
火源设置在模拟区域中央,位于入口300 m处,距离地面1.8 m。假设在初始时刻隧道内温度为20 ℃,隧道左端入口设为速度边界,风速方向垂直于入口断面,隧道出口设为压力边界。
3.2 临界风速的数值模拟研究
首先利用试验数据验证数值模型的可靠性。在处理数值模拟数据和试验数据时,将燃烧稳定后一段时间内的温度时均平均值作为该测点的温度。2种测试方法的初始环境温度不同,模型试验时的环境温度为18 ℃,数值模拟设置的环境温度为20 ℃,因此,应对比测点温度与环境温度的差值。不同纵向风速下的温差实测值与模拟值比较见图 5,其中试验数据中的风速和距离已按照相似比例关系转化为实体隧道内的数据。从图5可见:当火源功率为15 MW时,不同纵向风速下拱顶下方烟气温度的实测值与数值模拟值基本吻合,大部分测点的误差在10 ℃以内,只有极少数测点的误差超过10 ℃,但在15 ℃以内,可以认为在各种火灾工况下,烟气温度的数值模拟结果可信;另外,火源上游45,90,135,180 m的温度实测值和数值模拟值随纵向通风的变化趋势一致,即都是在相同的纵向风速下趋于接近环境温度,因此,通过数值模拟获取火灾所需临界风速是可行的。

图5 不同纵向风速下的温差实测值与模拟值比较Fig.5 Comparison of test results and simulation results of temperature difference at different longitudinal wind velocities
模拟分析了火源功率为5,10,15,20,25和30 MW下抑制烟气回流所需的临界风速。以15 MW火源功率为例,纵向风速为2和3 m/s时火源附近的温度分布如图6所示。从图6可以看出,在2 m/s的纵向风速下,火源上游拱顶下方发生烟气逆流;当纵向风速为3 m/s时,火源上游温度均在常温附近,得到15 MW火源功率下临界风速为2~3 m/s。与试验研究方法相同,数值模拟时,在风速为2~3 m/s范围内以0.1 m/s的跨度调整风速。模拟结果表明:5,10,15,20,25和30 MW火源功率下的临界风速分别为2.0,2.3,2.7,3.0,3.3 和 3.6 m/s。

图6 起火后约600 s火源附近的温度分布图Fig.6 Temperature distribution near fire source 600 s after ignition
4 结果分析
将数值模拟计算获得的临界风速代入式(9),求得5,10,15,20,25 和30 MW 火源功率下 k分别为 0.933,0.866,0.897,0.915,0.942,0.972,取算术平均值k=0.92。因此,临界风速公式为:

基于热物理学得出的临界风速理论模型与Heselden等[1−2]的研究成果是一致的。
根据本文模型以及Wu和Bakar模型可得到广深港狮子洋水下铁路隧道内的临界风速的预测结果,同时,在试验中测量了火源功率为10,15和20 MW时狮子洋隧道内的临界风速。模型预测结果、试验结果、数值模拟结果以及Wu和Bakar的模型预测值对比如图7所示。从图7可见:模型预测结果、试验结果、数值模拟结果三者非常接近,当火源功率<50 MW时,模型预测结果与Wu和Bakar的研究成果具有相同的发展趋势,临界风速都是随着火源功率的增大而增大,而且随火源功率变化的幅度一致。存在差距的原因可能是隧道中车体体积较大,火源离地面有一定的高度,而Wu和Bakar的模型中并没有考虑火源高度对临界风速产生的影响。与Wu和Bakar模型结果相比,模型预测结果偏安全,验证了模型的可靠性。当火源功率>50 MW时,模型预测结果继续随着火源功率的增大而增大,而Wu和Bakar模型的临界风速趋于定值。模型预测结果同Kennedy等的半经验公式一样不适合预测火源功率较高工况下的临界风速,只适合小火源功率下临界风速的预测。

图7 理论模型与模型试验及前人经验公式得到的结果对比Fig.7 Comparison of critical velocities obtained by theoretical model, test results and previous achieved formula
临界风速不再随火源功率变化的现象可以根据McCaffrey[15]的火焰分区理论来解释,间歇火焰区流速恒定,当火源强度超过一定范围时,间歇火焰区向上发展直接撞击顶板,浮力的影响被大大削弱,临界风速对火源功率的变化不再敏感,而是趋于一个定值。虽然羽流理论可以解释火灾的发展与临界风速的关系,但是并不能根据间歇火焰区撞击拱顶后的物理状态来预测这个定值,需要进一步研究。
5 结论
(1) 对控制隧道火灾烟气蔓延的临界风速进行了理论分析,建立的临界风速模型与基于Froude数获得的半经验公式一致。
(2) 以广深港狮子洋水下铁路隧道为背景,通过缩尺模型试验和数值模拟计算对水平隧道火灾临界风速进行了研究,并确定了理论模型中的待定系数为0.92。
(3) 临界风速理论模型预测结果与模型试验数据非常接近,当火源功率较小时,与Wu和Bakar的研究成果具有相同的发展趋势,各个数据偏差不大,验证了理论模型的可靠性,可为隧道火灾临界风速的确定提供指导。
(4) 本文构建的理论模型不适合预测火源功率较高工况下的临界风速,下一步的研究工作将继续从热物理方面研究间歇火焰区撞击拱顶后的物理状态,建立预测大火源功率下临界风速的模型。
[1] Heselden A J M. Studies of fire and smoke behaviour relevant to tunnels[C]//Stephens H S, British Hydromechanics Research Association. Proceedings of the Second International Symposium of Aerodynamics and Ventilation of Vehicle Tunnels.Bedford: British Hydromechanics Research Association Fluid Engeering, 1977: 1−18.
[2] Danziger N H, Kennedy W D. Longitudinal ventilation analysis for the glenwood canyon tunnels[C]//Stephens H S, Goodes D H,British Hydromechanics Research Association. Proceedings of the Fourth International Symposium Aerodynamics and Ventilation of Vehicle Tunnels. Bedford: British Hydromechanics Research Association Fluid Engeering, 1982: 169−186.
[3] Oka Y, Atkinson G T. Control of smoke flow in tunnel fires[J].Fire Safety Journal, 1995, 25(4): 305−322.
[4] Atkinson G T, Wu Y. Smoke control in sloping tunnels[J]. Fire Safety Journal, 1996, 27(4): 335−341.
[5] Kunsch J P. Critical velocity and range of a fire-gas plume in a ventilated tunnel[J]. Atmospheric Environment, 1999, 33(1):13−24.
[6] Wu Y, Bakar M Z A. Control of smoke flow in tunnel fines using longitudinal ventilation systems: A study of critical velocity[J].Fire Safely Journal, 2000, 35(4): 363−390.
[7] Li J S M, Chow W K. Numerical studies on performance evaluation of tunnel ventilation safety systems[J]. Tunnelling and Underground Space Technology, 2003, 18(5): 435−452.
[8] Vauquelin O. Parametrical study of the back flow occurrence in case of a buoyant release into a rectangular channel[J].Experimental Thermal and Fluid Science, 2005, 29(6): 725−731.
[9] Roh J S, Ryou H S, Kim D H, et al. Critical velocity and burning rate in pool fire during longitudinal ventilation[J]. Tunnelling and Underground Space Technology, 2007, 22(3): 262−271.
[10] 张兴凯. 地下工程火灾原理及应用[M]. 北京: 首都经济贸易大学出版社, 1997: 189−193.
ZHANG Xingkai. Fire principles and their application in underground engineering[M]. Beijing: Capital University of Economics and Business Press, 1997: 189−193.
[11] 王英敏. 矿内空气动力学与矿井通风系统[M]. 北京: 冶金工业出版社, 1994: 271−273.
WANG Ying-min. Mining Dynamics and mine ventilation system[M]. Beijing: Metallurgy Industry Press, 1994: 271−273.
[12] Vauquelin O. Experimental simulations of fire-induced smoke control in tunnels using an “air-helium reduced scale model”:Principle, limitations, results and future[J]. Tunnelling and Underground Space Technology, 2008, 23(2): 171−178.
[13] Hu L H, Huo R, Chow W K. Studies on buoyancy-driven back-layering flow in tunnel fires[J]. Experimental Thermal and Fluid Science, 2008, 32(8): 1468−1483.
[14] Lin C J, Chuah Y K. A study on long tunnel smoke extraction strategies by numerical simulation[J]. Tunnelling and Underground Space Technology, 2008, 23(5): 522−530.
[15] McCaffrey B J. Purely buoyant diffusion flames: some experimental results[R]. Washington DC: National Bureau of Standards, 1979: 10−25.
(编辑 赵俊)
Theoretical model of critical wind velocity in horizontal tunnel fires
XU Zhisheng, ZHAO Hongli, LI Hong, JIANG Xuepeng, LI Dong
(School of Civil Engineering, Central South University, Changsha 410075, China)
From the view of thermal physics, the critical condition for forming a reverse stratified layer was analysed, and a critical wind velocity model was set up for controlling smoke spreading in railway tunnel fires. The critical wind velocity in horizontal tunnel fires was studied through reduced-scale model tests and numerical simulation, and the undetermined coefficient in the theoretical model was ascertained. The theoretical value of the critical ventilation velocity was compared with the predictions by Wu and Bakar. The results show that the critical wind velocities predicted by theoretical model are in a good agreement with the corresponding experimental results. Wu and Bakar’s model underestimates the critical wind velocity in tunnel with pool fire, and the proposed theoretical model is not appropriate for predicting the critical wind velocity in tunnel fires at high heat releasing rate.
tunnel fires; critical wind velocity; theoretical model; reduced-scale model test; numerical simulation
X928.03,U459.2
A
1672−7207(2013)03−1138−06
2012−03−21;
2012−06−15
铁道部科技研究开发计划项目(2006G007-A-1,2006G007-C-1)
赵红莉(1986−),女,河南商丘人,博士,从事隧道通风排烟的研究;电话:0731-82656625;E-mail: zhaohonglixh@126.com

