基于电路法的优化式着色算法分析
张可为,申群太
(1. 中南大学 信息科学与工程学院,湖南 长沙,410008;2. 湖南工程学院 电气信息学院,湖南 湘潭,411101)
基于电路法的优化式着色算法分析
张可为1,2,申群太1
(1. 中南大学 信息科学与工程学院,湖南 长沙,410008;2. 湖南工程学院 电气信息学院,湖南 湘潭,411101)
提出一种基于优化形式的着色框架,并构建其等效求解电路,从而把着色问题转化为电路中节点电位的求解。设计一种能调节物体间颜色过渡带宽度的改进算法,并对其着色特性与现有混色算法进行比较分析。实验结果表明:根据电路理论中的基尔霍夫电流定律,证明了现有的2种着色算法等价;优化式着色实际上是一种混色过程,其混色权重等于像素随机游走的首达概率。优化式着色算法既能获得均匀的颜色渐变特性,又可以在物体间作很好的颜色区分。
着色;电路法;混色特性
着色指利用计算机辅助对黑白图像添加色彩成为彩色图像的技术。由于彩色图像具有更丰富的视觉表现力,所以图像着色广泛地应用于旧照片、老电影翻新以及医学、遥感等领域。传统的着色方法先将图像分割成块再分块涂上颜色,自动分割算法难以精确确定模糊、复杂的区域边界,需靠人工区隔,为此引入一些交互式分割方法,如贾云涛等[1]采用图切分,Liu等[2]利用随机游走分割等方法进行着色。但基于分割的着色结果呈严格的颜色分块,块间没有颜色过渡带,着色效果较生硬,在处理平缓颜色渐变时问题更严重。另一类方法是通过从彩色参考图像实现颜色迁移完成图像着色[3−4]。该技术适用于不同颜色区域具有不同灰度纹理的图像(否则用户必须指定匹配块来引导像素搜索),但用户对结果的控制非常不直接:要求参考图不仅具有所需的全部颜色,而且各颜色的区域纹理必须与对应的待着色区域相似,另外,对着色结果中问题区域调整非常困难。近年来出现的扩展型着色方法不仅可以直接选色,也便于修改,而且避免了分割式出现的颜色分块,它通过将用户在图像局部添加的颜色涂抹扩散至整幅图像完成着色。扩展型着色按扩展机理大致分为 2类:一类是混色式扩展,如 Yatziv等[5]将图像着色过程看作各颜色涂抹在每个像素上的混色,而混色权值取决于该像素至各类涂抹的最短路径距离(距离越短对应于权值越大),李志永等[6]用不平度取代最短路径距离,而Kawulok等[7]采用竞争性最短路径。最短路径法着色在大面积颜色渐变区的均匀性欠佳,原因在于图像中灰度的细小变化也会造成支路选择的很大不同,使得着色结果对光照比较敏感。另一类为优化式扩展方式,通过假设相邻像素满足指定的局部关系模型,把着色问题转化为约束优化问题,如 Levin等[8]假定每个像素的颜色可以表示成周围像素的加权平均和,由此构建一个全局代价函数,而用户的涂抹作为约束条件。并转化为线性稀疏系统求解。而 Liu等[9]则通过假设灰度相近的相邻像素其颜色差异应该越小,构建出另一个全局代价函数,并引入机器学习中的半监督学习求解。优化式算法得到广泛应用,但这种基于局部关系模型的扩展方式,难以了解算法的全局特性诸如着色结果与颜色涂抹的关系问题,另外优化式扩展往往对涂抹的数量与位置敏感,特别在物体交界区域,需要用户添加大量涂抹,增加了用户负担。尽管一些后续算法通过加入边缘信息[10−11]、非局部均值信息[12]来提高算法的鲁棒性,但改进质量依赖于检测精度。本文作者首先将优化式着色纳入同一个框架内,并对其着色结果与颜色涂抹的关系做定量分析,提出一种灵活性更高的算法。
1 问题描述
首先提出一种优化式着色的框架,并将图像着色问题转化成电路节点电位的求解,在此基础上分析 2种优化着色算法的等价性。
1.1 优化式着色方法的框架及电路法求解
黑白图像只记录了彩色原始场景的亮度信息,图像着色本质上是把图像中像素的灰度用三维颜色矢量取代,意味着相同的亮度允许映射为不同的颜色,所以着色是一个“病态”问题,不具有唯一解。为了降低这种映射的不确定性应引入颜色约束,颜色迁移型着色的约束体现在选择参考图像,而扩展型则表现为在图像上添加颜色涂抹。
除颜色约束外,图像的着色效果应尽量悦目自然,为此要求色度变化与灰度变化尽量一致:均匀灰度区域的色度变化小,而边缘等灰度剧烈变化的区域色度变化的可能性大。
为了避免着色过程中颜色与灰度间产生混淆,应将颜色与灰度分开,图像着色常用 YUV颜色空间,其中Y为灰度通道,而U和V为两色度通道,而着色的任务就是结合图像Y通道信息,把涂抹像素上的U,V信息自动扩散到整幅图像,所以最佳的着色情况应该满足一致性要求,即灰度越相似的相邻像素,其色度(包括U,V)差异应该越小。由于U与V相互独立,且计算方法相同,因而可统一用色度C表示。通过设计以下Gibbs能量函数J(C),求解C的最佳值分布可以表示为最小化该能量函数的过程,
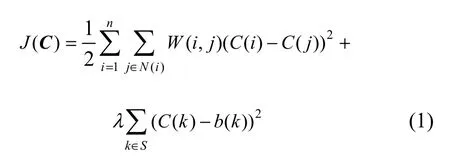
其中,等式右边第1项为光滑项,衡量与一致性假设的差异;第2项为数据约束项,λ为约束系数,反映涂抹像素最终的色度与初始色度的差异;n为像素总数,S为涂抹像素集合,b表示图像初始色度;N(i)代表像素i的邻居像素集合,即像素i周围一圈8个像素(i在图像边缘时相邻像素会减少), j为该集合中的一个像素;W为相似度矩阵,元素W(i, j)用来衡量像素i和j间相似程度,只有当i和j位置为近邻时,W(i, j)才可能为非0值,计算方法采用用宽度为σ的高斯核权值函数

其中:Y(i)表示像素i的灰度。由于W(i, j)=W(j, i),所以W为对称阵。


若要求涂抹像素在着色过程中尽量保持不变,可调整约束系数λ→∞,整理后得到

其中:In为n维单位矩阵。
下面将上述着色问题转化成电路的电位求解。
根据用户添加的涂抹以及图像像素间关系组建一个外加直流电源的电阻网络:以像素拓扑位置作为节点,任意两相邻节点i和j间电阻等于像素间相似度的倒数,即涂抹像素的初始色度作为外接直流电源的电压;而电源内阻RS设为1/(2λ),如图1所示。

图1 优化式着色的等效电路图Fig.1 Equivalent circuit of optimization-based colorization
该电路总功耗P由电阻网络功耗与电源功耗2部分组成,
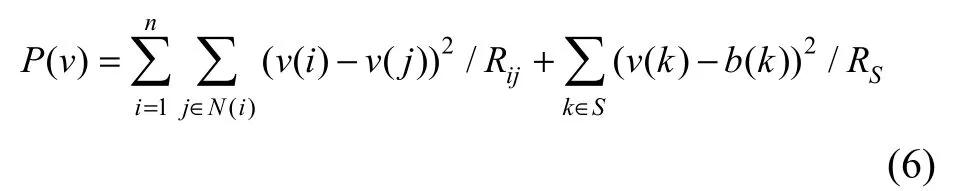
其中,v(i)为节点i电位。
由于电路中所有节点的电位分布满足最小能耗原理,故电位分布可以表示为最小化能耗的过程:
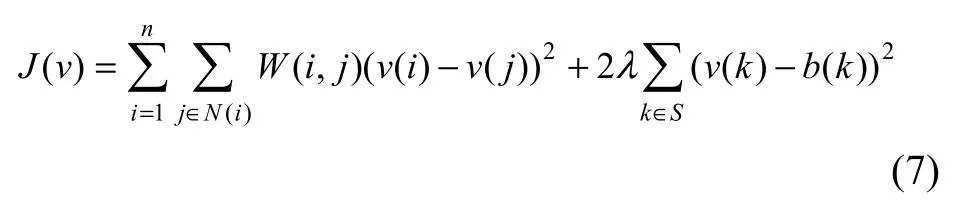
与式(1)一致,它表明电路中任意节点的电位与其对应的像素的色度相等,即要获得图像像素的色度可通过转化为构建相应电路求解其节点电位来完成,所以称该电路为优化式着色的等效电路。
另外,约束系数λ通过改变电源内阻影响各节点电位。λ越大,电源内阻越小,而当λ→∞,内阻短路,外接电源等效为理想电源,此时涂抹像素电位等于外接电源电位,对应于涂抹像素在着色过程中保持不变的情形。
1.2 新框架与Levin着色算法、半监督学习着色算法的关系
Levin着色算法的基本假定为每个未涂抹像素的颜色均可以用周围像素的加权平均和表示,即
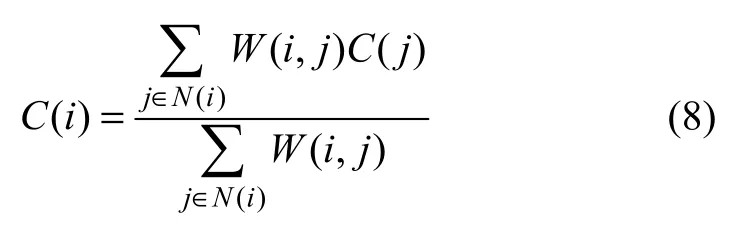
而考察上述电路,根据基尔霍夫电流定律,电路中经过任意节点的电流总和为0 A,结合欧姆定律,将任意节点i及相邻节点的电位表述为
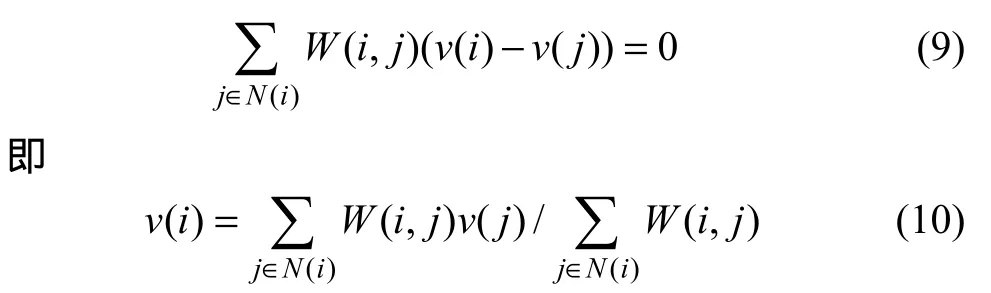
它表明任意节点电位可表示成相邻节点的加权平均,说明任意像素的色度均可以表示成邻域像素颜色的加权平均,这正是Levin算法的假定,说明新算法与Levin算法等价。
Liu等[9]把着色问题转化为机器学习中的半监督学习,将C的最佳分布表示为最小化以下能量函数的过程。
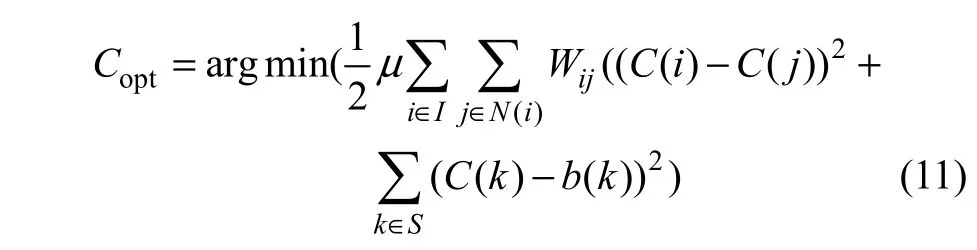
其中,μ→0。
与式(1)相比可知:Liu的算法结果与式(1)在λ→∞的情况对应,同时也表明半监督学习法着色算法与λ→∞时的Levin算法等价。
2 基于首达概率的混色式着色算法
2.1 优化式着色算法的混色特性
优化式着色通过求解约束优化问题实现着色,其结果与颜色涂抹的关系不直观,相反,混色式将图像着色结果看作不同颜色的涂抹在每个像素上的混色,而且对混色权值赋予明确的意义。首先引入混色和首达概率的概念,然后利用等效电路证明优化式着色算法也具有混色特性。
定义 1 混色指图像的像素色度均可以表示成涂抹色度的加权平均和,且权值非负。


其中:x必须为非负的行归一化矩阵。
定义 2 首达概率指从一个像素出发随机游走,首次遇到的涂抹像素属于某种颜色涂抹的概率。
若定义任意像素i首达其中任意一种涂抹r的概率为p(i,r),则p(i,r)具有以下性质:
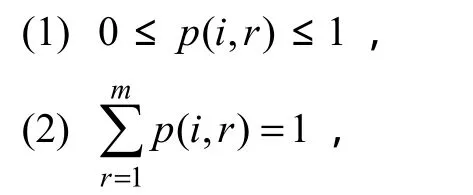
首达概率可以通过下列电路求解[13]:若定义等效电路,其电阻网络与图1一致,将任意一个电源——如第r种涂抹电源改为单位电源,且使其单独作用(其他涂抹电源接地),用y(i,r)表示此时在指定像素节点i的电位,则有 p(i,r) =y(i,r)。
结合上述定义讨论优化型着色的混色特性。
定理 1 优化型着色也是一种混色式着色方法,且每种颜色涂抹所占的混色权重等于像素至该种涂抹的首达概率。
证明 由于等效电路为电阻网络组成的线性电路,根据叠加原理,所有涂抹电源同时作用时在一电路节点产生的电位应该等于每种涂抹电源单独作用所得电位的代数和。取vr(i)表示第r种涂抹电源单独作用时在节点i产生的的电位,则


这种混色称为概率式混色。利用式(3)可以找出首达概率的计算方法。由于初始颜色b可表示为涂抹的混色形式,b=Mc,其中 M 为n×m矩阵,其元素M(i, j)为

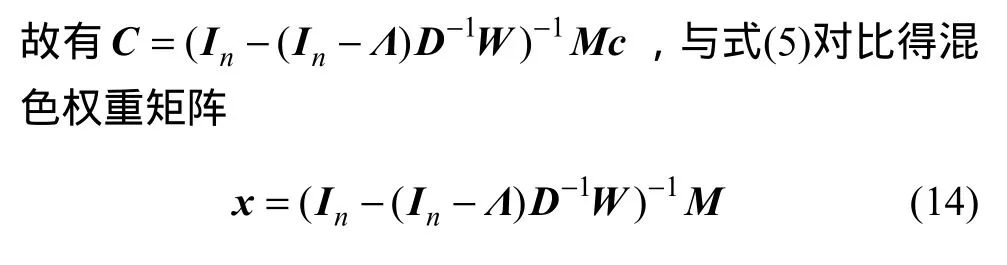
2.2 物体间过渡带宽度调节
在自然图像中,物体间出现颜色过渡带主要有几个原因:运动模糊效应、光学模糊效应以及离散化伪影等,这些效应所形成的过渡带较窄。但扩展型着色在涂抹较少以及距离物体边界较远时,难以区分边界,容易出现过宽的过渡带。以最短路径为例,当像素至物体内涂抹距离过远时,它难以区分2种灰度差的累加——经过本物体内长距离的低灰度区和穿过短距离的边界高灰度区,从而难以识别物体边界。同样,概率法混色的权重也受制于2个因素:距离和单步转移概率,如果物体内涂抹距离过远也会大大降低像素至该类标志的首达概率,从而降低该涂抹对应的混色权重。传统的解决方法为由用户在交界处附近两边设置大量涂抹,既费工也费时,而下面直接利用调节混色权重来控制过渡带宽度,从而提高物体边缘处的着色质量。
为了减弱空间距离对识别物体边界的影响,引入归一化指数函数,

其中:B为混色因子,当B>1时可以增加本物体的涂抹的混色比重。该函数在文献[5]以及抠图中都有应用[14−15]。
以 2种涂抹(m=2)为例给出权值映射的结果见图2。由图2可见,x相同时,随着B增大,新权值xB趋近于0或1,过渡速度加快,过渡带变窄。
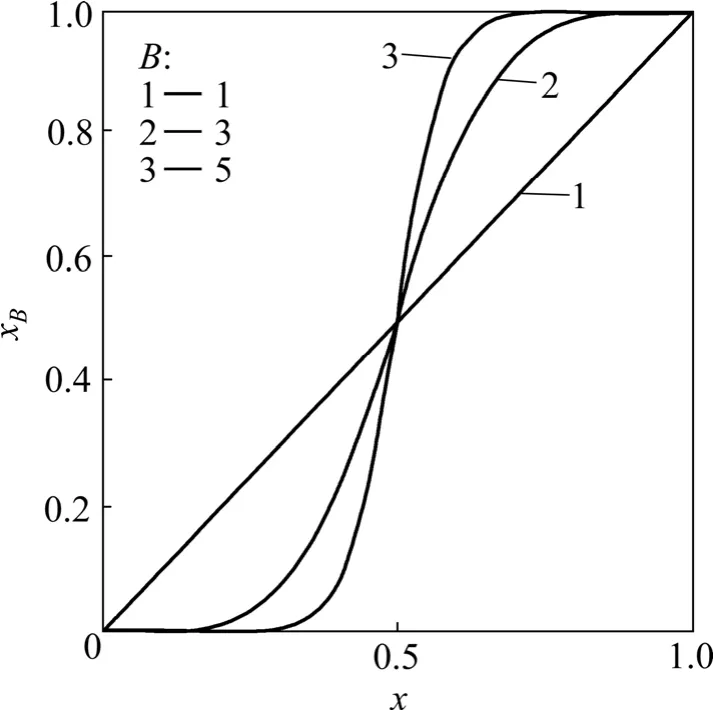
图2 权值映射关系Fig.2 Corresponding relation of weight mapping
2.3 算法描述
利用优化式扩展的混色特性以及混色式扩展在边界过渡带宽设置的灵活性,将优化式着色算法改造成一种混色算法。算法步骤如下:
(1) 添加颜色标记。用户在图像的均匀颜色区域添加少量的颜色涂抹。
(2) 转换颜色空间。将标示后图像转换成YUV颜色空间,以便于将彩色信息与灰度信息分开(也可以采用其他颜色空间如 YIQ,Lab,只要能将灰度与色彩分开即可)。
(3) 建立相似度矩阵。
(4) 采用式(10)求出混色权重。
(5) 权值映射混色。先采用式(15)映射,然后用公式 C = xBc混色。
(6) 输出图像整合。将传播获得的 U,V通道值与图像的灰度结合转换回 RGB空间,从而整合成最终的改色图像。
3 实验结果与数据分析
扩展式着色的质量主要取决于2个因素:物体间颜色区分和物体内颜色渐变的均匀性。下面通过实验对新算法与Levin算法、最短路径混色算法进行比较。鉴于着色的结果与各颜色涂抹所占的混色比例具有一一对应的关系,算法的着色质量可以通过各颜色在图像中的混色比例分布反映,为此通过归一化灰度图来表示混色比例分布:图中像素的灰度越大表示指定颜色所占的混色比例越大,而其他颜色所占比例越小。黑色对应于 0,表示像素不含该种颜色,而白色对应于混色权重为100%,表示完全由该颜色组成。
着色算法对物体区分的效果比较如图3所示。用户希望将灰色波浪带添加红色,其他部分为黄色。添加的涂抹见图3 (a),而图3 (b)~(d)为新算法取不同B值时获得的黄色混色权重图。B=1对应于Levin算法和基于半监督学习的着色算法,从混色权重分布反映出着色图像中存在黄色扩散严重不足和红色发散的现象,原因在于该算法在物体交界处的区隔性不太强,对涂抹位置与数量敏感,导致在距涂抹位置较远处着色质量不高。但随着B的增大,边界的过渡带变窄,着色效果得到改善。可以看到:当B=3时,2种颜色已经可以很好地区隔。

图3 混色因子B对着色的影响Fig.3 Influence of factor B on visual result

图4 2种混色法在平缓渐变区的着色Fig.4 Colorization on gentle transition area
图4所示为2种混色法在平缓渐变区的着色效果比例。为了形成红花绿叶、花蕊至花瓣颜色渐变的着色结果,用户添加3种涂抹,如图4(a)所示。从图4可以看到,2种混色方法对花与叶之间都区隔得很好,但在花瓣内形成颜色平缓变化的区域着色效果差异较大。采用最短路径的着色效果均匀度较差,原因在于最短路径法的混色权重只考虑最短路径,相当于在等效电路中找出一条最小串联电阻的支路进行信息传播,由于只结合串联特性,若区域内灰度梯度较小,光影的细小变化也会造成支路选择的很大不同,使得着色结果对光照比较敏感;而概率混色算法在计算最短路径时兼顾了流量,具有串并联特性,与最短路径法相比,可以获得更好的颜色渐变特性。
4 结论
(1) 提出一种一般性优化着色框架后建立其等效电路,从而把着色问题转化成电位的求解问题。在此基础上利用基尔霍夫定律证明了Levin基于加权平均和的优化算法与基于半监督学习的着色算法等价。
(2) 采用齐次定理、叠加原理等论证了优化着色算法本质上也是一种混色算法,图像中每个像素的颜色由各初始颜色涂抹按比例权重混色而成,其中各颜色的混色权重等于像素随机游走首先到达该颜色涂抹的概率。
(3) 设计了一种兼具优化、混色法优点的着色算法,既能在平缓过渡区域获得均匀的着色效果,也可以通过控制过渡带宽加强算法对涂抹数量与位置的鲁棒性。
[1] 贾云涛, 胡事民. 基于图切分的交互式图像染色算法[J]. 计算机学报, 2006, 29(3): 508−513.
JIA Yuntao, HU Shimin. Interactive graph cut colorization[J].Chinese Journal of Computers. 2006, 29(3): 508−513.
[2] LIU Xiaoming, LIU Jun, FENG Zhilin. Colorization using segmentation with random walk[C]//Proceedings of International Conference on Computer Analysis of Images and Patterns,Berlin: Springer-Verlag, 2009: 468−475.
[3] Welsh T, Ashikhmin M, Mueller K. Transferring color to grayscale images[J]. ACM Transactions on Graphics, 2002,21(3): 277−280.
[4] AN Xiaobo, Pellacini F. User-controllable color transfer[J].Computer Graphics Forum, 2010, 9(2): 263−271.
[5] Yatziv L, Sapiro G. Fast image and video colorization using chrominance blending[J]. IEEE Transactions on Image Processing, 2006, 15(5): 1120−1129.
[6] 李志永, 滕升华, 杜坤, 等. 基于不平度颜色混合的图像彩色化方法[J]. 电子信息学报, 2008, 3(3): 514−517.
LI Zhiyong, TENG Shenghua, DU Kun, et al. Colorization based on unevenness in chrominance blending[J]. Journal of Electronics & Information Technology, 2008, 3(3): 514−517.
[7] Kawulok M, Smolka B. Competitive image colorization[C]//Proceedings of 2010 IEEE 17th International Conference on Image Processing, HongKong: IEEE Press, 2010: 405−408.
[8] Levin A, Lischinski D, Weis Y. Colorization using optimization[J]. ACM Transactions on Graphics, 2004, 23(3):689−694.
[9] LIU Beibei, Lu Zheming. Image colourisation using graph-based semi-supervised learning[J]. IET Image Process, 2009, 3(3):115−120.
[10] Huang Y C, Tung Y S. Chen J C, et al. An adaptive edge detection based colorization algorithm and its applications[C]//Proceedings of the 13th annual ACM international conference on Multimedia, Singapore: ACM, 2005: 351−354.
[11] NIE Dongdong, MA Lizhuang, XIAO Shuangjiu, et al.Grey-scale image colorization by local correlation based optimization algorithm[C]//Proceeding of Visual Information and Information Systems, Berlin: Springer-Verlag, 2005: 13−23.
[12] YAO Chen, YANG Xiaokang, WANG Jia, et al. Patch-driven colorization[J]. Optical Engineering, 2010, 49(1): 1−5.
[13] Grady L. Random walks for image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2006,28(11): 1768−1783.
[14] Levin A, Rav-Acha A, Lischinski D. Spectral matting[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2008,30(10): 1699−1712.
[15] Rhemann C, Rother C, Gelautz M. Improving color modeling for alpha matting[C]//Proceedings of the British Machine Vision Conference, Ledds: British Machine Vision Association, 2008:1155−1164.
(编辑 赵俊)
Optimization-based colorization algorithms based on circuit principle
ZHANG Kewei1,2, SHEN Quntai1
(1. College of Information Science & Engineering, Central South University, Changsha 410008, China;2. College of Electrical & Information Engineering, Hunan institute of Engineering, Xiangtan 411101, China)
A general frame for colorization based on optimization was put forward, and followed by its equivalent electrical circuit which formulates colorization process as evaluating potential of all nodes. An improved algorithm which is capable of adjusting width of transition area in between two objectives was designed. And then the colorization feature was compared with that of existing chrominance blending methods. The results indicate that it has been proved that the two existing methods are equivalent according to Kirchhoff’s current law, and the optimization-based colorization can be also viewed as that of chrominance blending where every blending weight of each pixel equals this pixel’s first-reach probability in its random walk to relevant kind of scribble. This proposed approach has provides good quality in both distinguishing from two objects and preserving homogeneous gradient colors inside.
colorization; circuit principle; chrominance blending
TP391.41
A
1672−7207(2013)03−1043−06
2012−02−15;
2012−05−21
湖南省教育厅科研项目(08c220)
张可为(1966−),男,湖南益阳人,博士研究生,讲师,从事图像处理及智能控制研究;电话:13187322670;E-mail: d10zhangkw@yahoo.com.cn

