不同铆测验设计下多维IRT等值方法的比较*
刘 玥 刘红云
(1四川省教育科学研究所,成都 610225) (2北京师范大学心理学院,北京 100875)
1 引言
在大型的教育测验中,常常会出现考核同一个内容的多个测验形式,为了实现这些测验分数之间的比较,会用到测验等值的方法。根据等值所依据的原理,一般可以分为经典测验理论(CTT)下的等值方法和项目反应理论(IRT)下的等值方法(Kolen&Brennan,2004)。其中,IRT等值方法又以其理论完善,等值关系简洁,且题目参数具有跨群体不变性等优势,而受到广泛关注。在大多数的标准测验中,考生的能力参数和题目参数是由单维IRT模型(UIRT)估计得到的,因此,基于单维IRT模型的等值方法已经得到了较为深入的研究(Kolen&Brennan,2004)。
然而,在现实情境里,测验通常会包含多维结构(Ackerman,1994;DeMars,2006;Reckase,1985)。在很多大型的教育评价项目中,对于一个概括性的能力的测量,通常会包含关于多个子学科(子能力)的题目。例如在关于学生科学能力的测验中,可能包含分别来自于物理,地理,生物等多个学科的题目。这时,传统IRT理论的单维性假设很容易遭到违背。基于单维IRT假设的参数估计和IRT等值结果会出现一定的偏差(Reckase,2009;Brossman,2010)。因此,许多研究者已经逐渐开展了对基于多维项目反应理论(MIRT)下等值方法的研究和探索。
迄今,很多研究已经将单维IRT下的等值方法推广到多维结构中。这些方法主要有多维均值/均值方法,均值/标准差方法(Yao,2011),IRT相等函数方法,Stoking-Lord(测验特征函数)方法,Haebara(项目特征函数)方法,直接方法(Oshima,Davey&Lee,2000),LL方法(Li&Lissitz,2000),Min的方法(Min,2003),NOP方法(Reckase&Martineau,2004)和同时等值的方法(Simon,2008)等。这些方法和单维IRT等值方法的主要区别是,多维IRT等值不仅需要调整不同测验量尺原点和单位大小的差异,还要进行量尺旋转和维度相关调整等一系列过程(Reckase,2009)。这些方法之间的主要区别在于它们计算参数转换矩阵的原理和方法不同。一些研究还基于题目参数的返真性对多维IRT等值方法进行了比较(Davey,Oshima,&Lee,1996;Li&Lissitz,2000;Oshima et al.,2000;Yao&Boughton,2009)。总的来说,大多数研究结果表明,Stoking-Lord(SL)方法和Haebara(HB)方法较为稳定,并且得到的等值结果更加准确(Davey et al.,1996;Oshima et al.,2000;Yao,2011;Simon&Davison,2008)。但是Yon(2007)的研究也证明,NOP方法对题目区分度的等值结果比多维Stoking-Lord方法准确。Brossman(2010)在提出多维IRT真分数等值和观察分数等值方法后发现,与单维IRT等值的规律相似,多维IRT真分数等值和观察分数等值表现出很高的一致性,仅在低分段和满分附近出现一定的差异。Simon(2008)对多维IRT同时等值和分别等值方法进行了比较研究,他们建议,当两组被试的能力水平差异不大且多维测验各维度间的相关较高时,同时等值的方法要优于分别等值。总的来说,关于多维IRT等值方法的比较还没有得出较为一致的结论。
进行多维IRT等值,数据结构必须符合以下两个条件之一(Angoff,1982;Davey et al.,1996):(1)测验之间包含相同的题目(铆测验);(2)有一批相同的考生同时参加了两个测验。在实践中,尤其是大规模测验中,铆测验设计应用得最为广泛。铆测验本身对等值结果有显著的影响。有学者认为,铆测验的选择必须尽可能代表整个测验的特征(Cook&Petersen,1987;Klein& Jarjoura,1985;Marco,Petersen,&Stewart,1983)。Kolen和Brennan(2004)曾建议,铆测验应当包含足够多的题目,经验的法则是铆题量至少为测验总题量的20%。Sinharay和Holland(2007)认为,铆题应当具有内容代表性,并且难度参数的均值与总测验相等,只是变异性略小。针对多维IRT等值,Yao和Boughton(2009)对同时含有多项选择题和结构性试题测验的多维IRT等值进行了考察,结果发现在铆测验中使用简单结构的题目(题目只属于其中一个维度)或与结构性试题分值相等的多项选择题,能够提高等值结果的准确性。Yao(2011)进而提出了一些在多维IRT等值中选择铆测验的标准,其中包括:铆测验的测验特征函数应当与整个测验接近,铆测验中各维度题目的数量应当与总测验中各维度题目的数量成比例等。其研究结果证明,按照所提出的标准选择铆测验,即使在每个维度只有2道铆题的情况下,多维Stoking-Lord方法也能得到较好的维度分和总分的等值结果。
尽管铆测验的选择在等值中至关重要,但是在多维IRT等值中,很少有研究关注在不同铆测验设计下各种多维IRT等值方法的比较(Yao&Boughton,2009)。另外,以往的研究主要关注题目参数的等值结果,很少有研究对能力参数的返真性进行比较。为了充分考察在不同的铆测验设计下,各等值方法的表现,从而为实践中多维IRT等值总结铆测验的设计原则和选择等值方法提供依据,本文在不同的铆测验设计下,采用模拟研究的方法对五种应用较广的多维IRT等值方法—— 均值/均值(MM)方法,均值/标准差(MS)方法,多维Stoking-Lord(SL)方法,多维Haebara(HB)方法,最小平方(LS)方法进行比较,旨在考察铆测验中题目数量和铆测验构成方式对不同等值方法的影响,主要解决以下几个问题:(1)在多维IRT等值中,五种常用等值方法的优劣;(2)铆测验的长度对等值结果的影响;(3)使用不同的策略选择铆测验(铆测验中各维度题目数量之比与总测验中各维度题目数量之比相同,铆测验中各维度题目数量相同)是否会对等值结果有影响。同时,还考虑了测验维度之间的相关和两个群体能力差异大小对等值结果的影响。
2 多维IRT模型及等值方法
2.1 两参数多维IRT模型

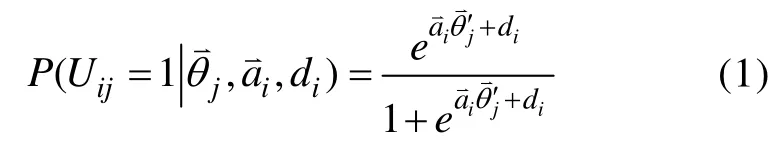
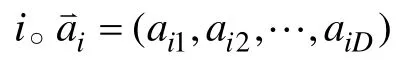
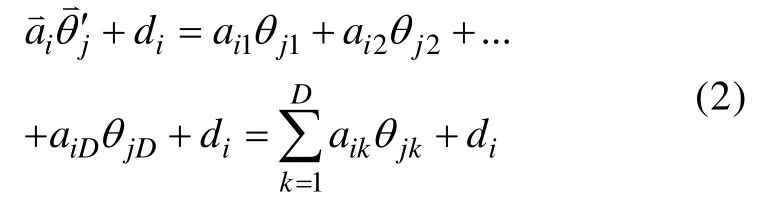
d
不同于单维IRT模型中的难度参数。多维IRT的难度参数定义为:
2.2 多维IRT等值
与单维IRT等值的原理类似,多维IRT等值的目的是找到合适的转换矩阵A
,B
,从而将不同测验的题目和能力参数等值到同一量尺上。使用转换矩阵进行量尺转换的公式为:
下面,介绍本研究采用的五种多维IRT等值方法。
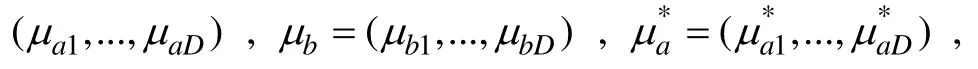



SL方法。
Oshima,Davey和Lee(2000)将单维IRT中的Stoking-Lord方法推广到多维结构的数据中。因此,对于含有两个维度的多维测验,多维SL等值方法求出将下面函数最小化时的转换矩阵A
,B
。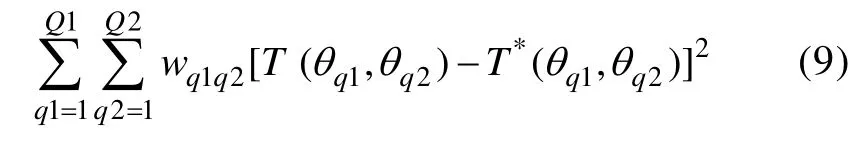

HB方法。
Oshima,Davey和Lee(2000)将单维IRT中的Haebara方法推广到多维结构的数据中。因此,对于含有两个维度的多维测验,多维Haebara等值方法求出将下面函数最小化时的转换矩阵A
,B
。

LS方法。
在LS方法中,题目参数的转换矩阵与之前的方法有一些区别,其定义如下(Li&Lissitz,2000):
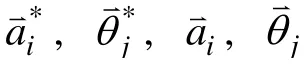
3 模拟设计
3.1 混合实验设计
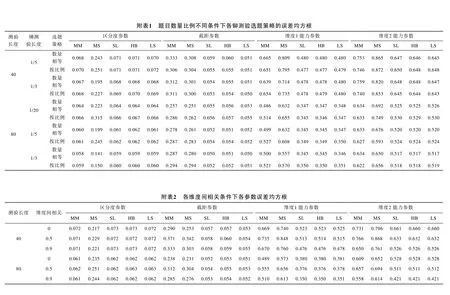
在研究中,由于五种多维IRT等值方法均会应用于每组需等值的模拟数据,因此,这是一个混合实验设计。组内变量为五种等值方法,组间变量为各种模拟条件。组间变量有6个。(1)测验长度:测验中所有的题目个数,分别取40和80两种情况。(2)两个维度题目数量的比例:有两个水平,分别为1:1(两个维度题目数量相等)和3:1(两个维度题目数量不等)。(3)铆测验长度:取三个水平,铆测验题目数量分别为全卷的1/20,1/5和1/3。(4)铆测验的选择策略:考虑了两种方法,即在每个维度中选取相等数量的题目组成铆测验和根据全卷中每个维度题目的数量,按比例选取铆题组成铆测验。(5)两个维度之间的相关:取三个水平r=0,0.5,0.9,分别代表无相关,中等程度相关和高相关。(6)等值群体的能力水平差异:分为两种情况,两组群体能力水平无差异(等组等值)和两组群体能力水平有差异(非等组等值)。在等组等值的情况下,两组被试的能力服从均值为0,标准差为1的多元正态分布;在非等组等值的情况下,参加基础测验组的被试能力服从均值为-0.5,标准差为1的多元正态分布,参加新测验组的被试能力仍服从均值为0,标准差为1的多元正态分布。组间变量(1)到(4)交叉形成了17种不同的铆测验设计,具体见表1。每种铆测验设计下,考虑两个维度之间的相关和等值群体能力的差异,模拟设计共有17×2×3=102种。
3.2 数据生成
使用R语言自编程序产生每种条件下的反应数据。每种条件下包括在基础测验和新测验上,各3000名被试对题目的反应,所有的题目均为0/1计分。产生数据所依据的模型为多维两参数Logistic模型,模型包含两个维度,并且测验符合简单结构。在各条件下,模拟数据的参数分布参照前人文献及实证研究经验。其中a ~N(0.8,0.2 ),b ~N(0,1 )
,该分布与ETS进行SAT测验的观察分数的边缘分布匹配,故可以与实际数据相比较(Bradlow,Wainer&Wang,1999)。每种设计条件下数据重复模拟30次。3.3 参数估计和等值
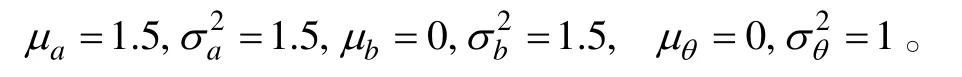
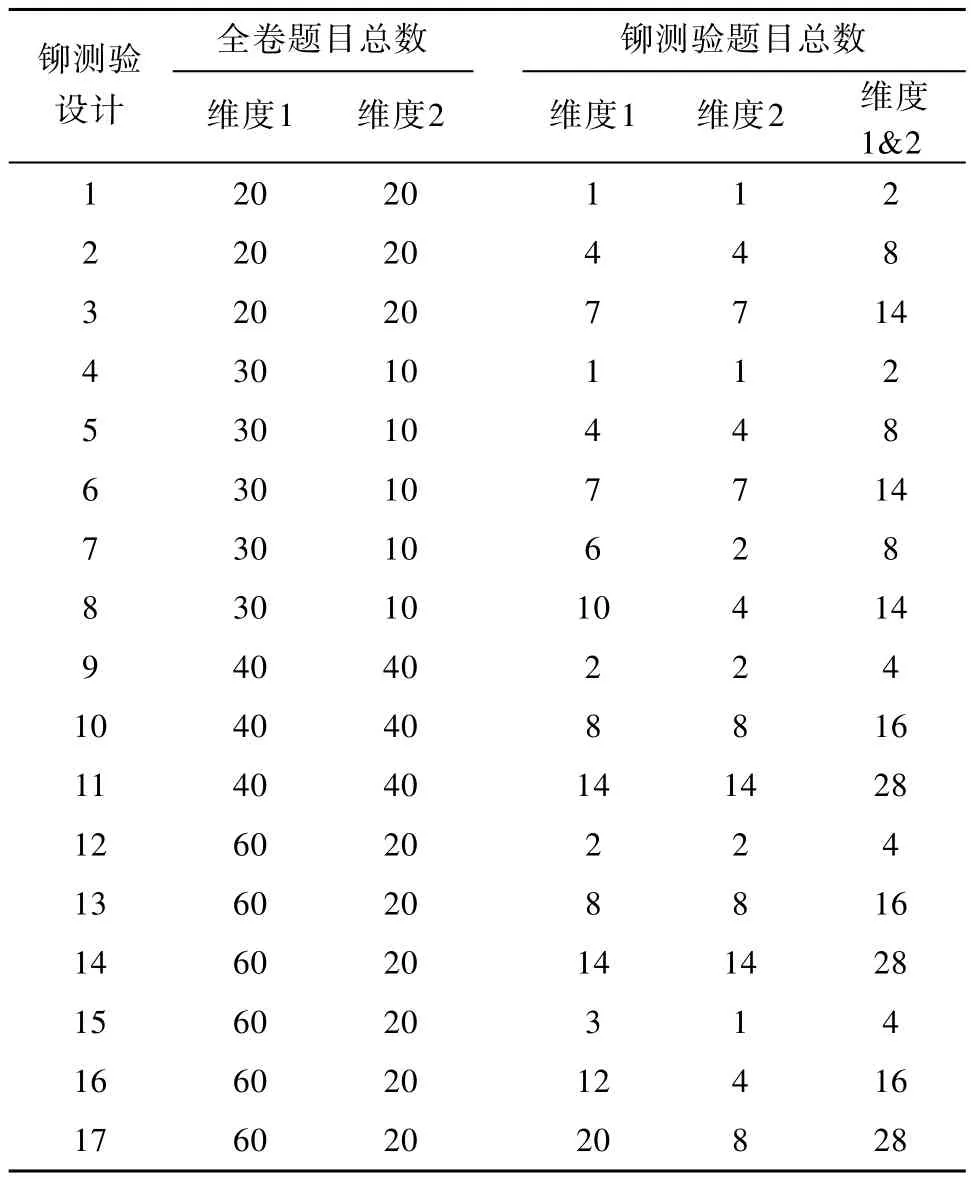
表1 不同铆测验设计
按照等值研究的步骤,研究采用了两步等值法(Kim&Cohen,1998;Kim&Cohen,2002)。第一步将新测验上的题目参数和能力参数转换到基础测验的量尺上。第二步将第一步中所有等值后的参数转换到真值的量尺上。在每种等值方法的条件下,第一步和第二步使用的方法完全相同。例如,在第一步中使用了MM方法将新测验的参数等值到基础测验的量尺上,在第二步中,以两套测验的所有题目为铆题,再次使用MM方法将等值后的参数转换到产生值的量尺上。
对于MM和MS方法,通过程序LinkMIRT(Yao,2004)计算转换矩阵A
和B
。对于SL,HB和LS方法,调用R中的软件包“Plink”完成等值(Weeks,2010)。根据前面介绍的两步方法,每次等值时,等值方法需重复使用两次以得到最后的参数结果。3.4 评价标准
本研究从四个方面评价各参数等值后的返真性:(1)偏差(Bias
),绝对偏差(MAE
),误差均方根(RMSE
),等值后结果与真值的相关(Correlation
)。偏差的意义是总体考察各条件下,各参数等值后结果是否有定向的偏差。其计算公式如下:
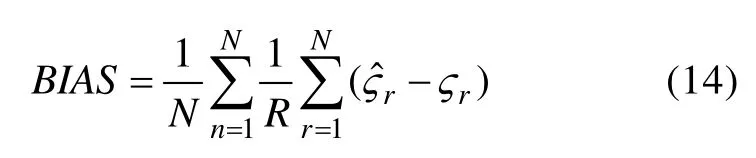

绝对偏差和误差均方根考察了各条件下,等值后的各参数值与真实值的差异的大小。这两个值越小,说明等值后各参数值与模拟的真实值越接近,等值效果越好。其计算公式如下:
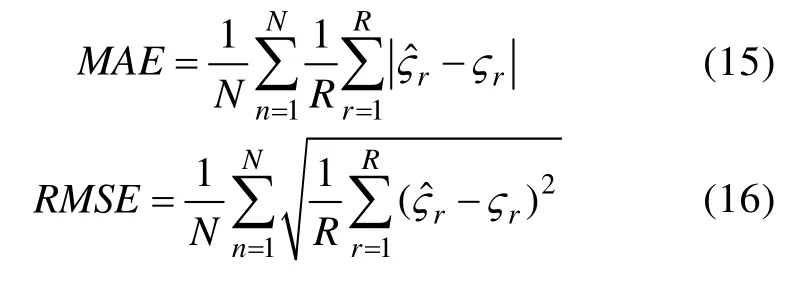
公式中各参数表示的意义与公式(14)相同。
等值后结果与真值的相关计算了各条件下,等值后各参数值与真实值的积差相关。它的意义是考察等值后参数结果与真实值的一致性水平。
4 结果
在参数估计过程中,所有设计因子的条件下模型均成功收敛。下面,从4个评价标准的角度呈现研究结果。
4.1 偏差
表2列出了各条件下各参数等值后的偏差。对于区分度参数,不同条件下得到的结果基本一致,MM,SL,HB和LS方法的偏差总体较小,而MS方法偏差较大。对于截距参数,总体来看,SL,HB和LS方法的偏差小于MM和MS方法;随着测验长度增加,各方法下截距参数等值偏差减小;两个维度的题目数量比例、铆测验长度、铆测验选择策略和测验维度之间的相关对截距参数等值偏差几乎没有明显影响;等值群体能力水平的差异对SL,HB和LS方法没有影响,对MM和MS方法有一定影响。对于能力参数,SL,HB和LS方法几乎没有偏差,明显小于MM和MS方法,且几乎不受其他因素的影响。MM和MS方法容易受其他因素的影响,如在非等组等值的情况下,MM和MS方法的偏差很大。
4.2 绝对偏差和误差均方根
由于绝对偏差和误差均方根具有较高的一致性,因此在本节的结果中,都参照误差均方根加以比较。
4.2.1 等值方法的比较
多维IRT等值方法对参数估计的精度有很大的影响。SL,HB和LS方法得到的等值后各参数精度较高,且这三种多维IRT等值方法几乎不受其他因素的影响,在各条件下等值结果相对稳定。MM方法对区分度参数等值的误差也较小,但是,MM方法对截距参数和能力参数的估计误差较大,MS方法对所有参数等值的误差都较大。
具体来说,对于题目参数和能力参数,在所有模拟因子的条件下,等值方法对误差均方根的影响仅依赖于等值群体的能力水平差异而不同。图1表示了等值群体的能力水平差异的不同水平下,五种等值方法得到的区分度参数、截距参数、能力参数的误差均方根。
从图1中可以看出,在等组等值的条件下,SL,HB和LS方法的结果略优于MM和MS方法;随着等值群体的能力水平差异增大,SL,HB和LS方法的结果保持稳定,而MM和MS方法的结果出现了较大的偏差。尤其对于截距参数和能力参数,MM和MS方法在非等组条件下的误差明显增大。
综上,从五种等值方法的比较结果可以看出,SL,HB和LS方法得到误差均方根显著小于MM和MS方法,在实际应用中应当作为首选方法。因此,在下面对铆测验设计的考察中,仅选取SL、HB和LS三种等值方法。
4.2.2 铆测验设计对题目参数等值结果的影响
区分度参数。
如图2所示,对于区分度参数,测验长度和铆测验长度对区分度参数估计的精度有较大的影响,即测验长度越长,铆测验长度越长,误差均方根越小。同时,测验长度和铆测验长度的交互作用对参数估计的精度也有较大的影响,在测验长度较短的条件下,铆测验长度仅为全卷的1/20时得到的误差均方根远大于其他条件。在相同的测验长度和铆测验长度下,铆测验选择策略对参数等值结果没有影响。另外,根据附表2~附表4,两个维度题目数量的比例对区分度参数等值结果没有显著影响。两个维度之间的相关和等值群体的能力水平差异对区分度参数等值结果没有显著影响。并且,在维度之间的相关或等值群体的能力水平差异不同的条件下,测验长度、铆测验长度和铆测验选择策略对参数等值结果的影响不存在差异。

图1 等值方法与等值群体的能力水平差异交互作用

图2 铆测验设计对区分度参数误差均方根的影响
截距参数。
铆测验设计对截距参数的误差均方根的影响与区分度参数类似。如图3所示,测验长度越长,铆测验长度越长,截距参数估计的误差均方根越小。另外,根据附表1,附表2,附表4,两个维度题目数量的比例,铆测验选择策略和维度之间的相关对截距参数的等值结果没有显著影响。不同的是,等值群体的能力水平差异对截距参数的等值结果有一定影响,等值群体的能力水平差异越大,误差均方根越大。在等值群体的能力水平差异不同的条件下,铆测验设计对截距参数等值结果的影响是相同的。4.2.3 铆测验设计对能力参数等值结果的影响
如图4所示,首先,题目数量较多的维度(维度1),其能力参数的等值误差均方根要小于题目数量较少的维度(维度2)。其次,对于两个维度的能力参数,测验长度和两个维度之间的相关的影响显著,即测验长度越长,相关越高,误差均方根越小。并且,对于题目数量较少的维度,相关对能力参数估计结果的影响更大。测验长度和相关还呈现出交互作用,当测验长度较短时,随着相关增加,误差均方根减小的幅度较大(维度1约0.047,维度2约0.134);当测验长度较长时,随着相关增加,误差均方根减小的幅度较小(维度1约0.031,维度2约0.107)。

图3 铆测验设计对截距参数误差均方根的影响

图4 测验长度和相关对能力参数误差均方根的影响
根据附表4,两个维度题目数量的比例对能力参数等值结果有显著影响,对于维度1能力参数,两个维度题目数量相等时的误差均方根要大于数量不等的条件,对于维度2能力参数,则与之相反。这是与每个维度题目数量相关的。在该因子的两个水平下,其他因子对能力参数等值结果的影响具有很强的一致性,并且,仅当两个维度题目数量的比例不同时,才能进行铆测验选择策略的比较。因此,为了仔细考察铆测验选题策略对能力参数等值的影响,本部分以两个维度题目数量不等的条件为例进行分析。表3列出了两个维度题目数量比例不同的条件下,SL方法得到的两个维度能力参数的误差均方根(HB和LS方法的结果与之类似)。
从表3中可以看出,当两个维度题目数量不等时,两种选题策略下的误差均方根在数值上非常接近。随着铆测验长度的增加,误差均方根有一定的减少,尤其对于维度2能力参数,在测验长度较长的条件下,该现象较为明显。等值群体的能力水平差异对能力参数估计结果没有影响。
4.3 等值后结果与真值的相关
在各种条件下,SL,HB和LS方法等值后各参数值与真实值的相关(区分度参数:0.923~0.998,截距参数:0.997~1.000,能力参数:0.697~0.987)大于MM和MS方法(区分度参数: 0.479~0.998,截距参数:0.829~1.000,能力参数:0.542~0.943),且更加稳定。说明SL,HB和LS方法的最后得到的等值结果与真实值存在较高的一致性。MM和MS方法得到的相关系数变异较大,在一些条件下,它们的结果甚至不可接受。对于SL,HB和LS方法,铆测验设计对区分度参数和能力参数相关值的影响与误差均方根的结果类似,而截距参数的相关在各条件下普遍较高(在0.998左右),不受其他模拟因子的影响。
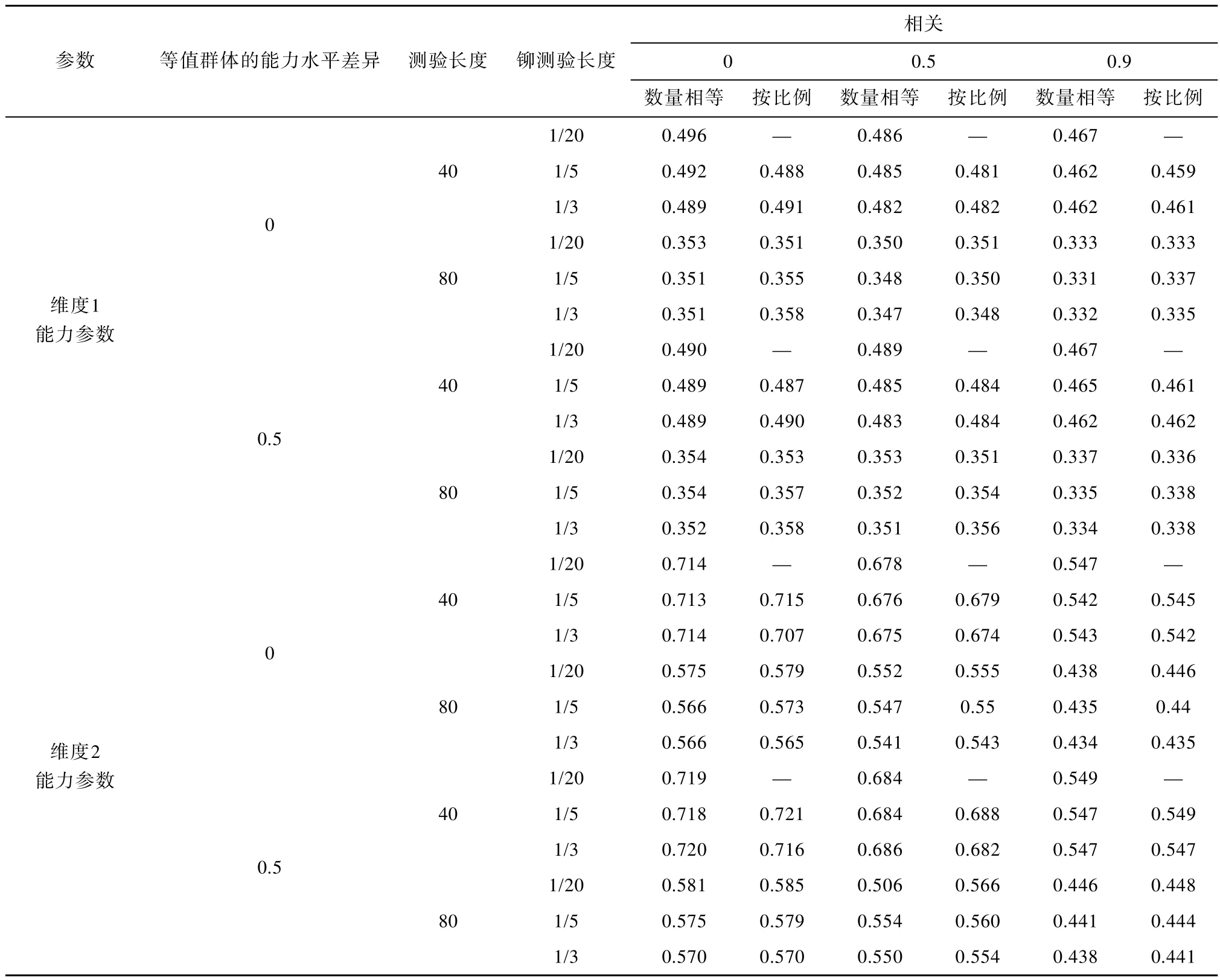
表3 两个维度题目数量比例不同条件下SL方法使用两种铆测验选题策略得到的能力参数误差均方根
5 讨论与结论
本研究基于含有两个维度的多维补偿性IRT模型模拟数据,比较了五种多维IRT等值方法在各铆测验设计下的表现,研究结果可以为多维IRT等值方法的比较及其影响因素的探索提供更详细的信息。
首先,通过对等值方法比较可以看出,SL,HB和LS方法得到的等值结果比MM和MS方法准确,特别是在非等组等值的情况下,其优势更为明显。在各模拟条件下,SL,HB和LS方法三种等值方法得到的结果较为稳定,这不仅与之前单维IRT等值的研究结果相呼应(Hanson&Béguin,2002),也与前人关于多维IRT等值的已有研究结果一致(Davey et al.,1996;Oshima et al.,2000;Yao,2011)。SL,HB和LS方法的优势可能仍在于它们在计算转换矩阵时,同时考虑了所有的题目参数。然而,除了MM方法对区分度参数等值的误差均方根较小之外,MM和MS方法在大多数情况下表现很差。其中,MS方法的误差均方根最大,这可能一方面由于该方法在等值过程中只考虑了难度参数,而另一方面,计算转换矩阵时需要用到难度参数的标准差,这个统计量本身不如平均数稳定,并且当铆题数量较小时,其标准差也极不准确。在应用LinkMIRT软件进行MM和MS方法等值时,计算出的转换矩阵A
中的元素有时很大。这与其他方法的结果存在显著差异。回顾MM和MS方法的原理,可知转换矩阵A
为对角矩阵,即对角线之外的元素均为0。但是我们在估计参数时,没有加入维度之间独立的假设,所以在计算转换矩阵时理应考虑维度之间的相关。这两种方法没有能够将维度之间的关系纳入转换矩阵的计算中,这可能是它们的结果出现异常值的一个原因。因此,在实际应用中最好选用SL,HB和LS方法进行多维IRT等值。其次,在选择 SL,HB和LS方法的前提下考虑不同铆测验设计的影响。对于第一个研究问题,铆测验长度对区分度参数,截距参数都有一定的影响。当测验长度较短时,如果铆测验长度仅为全卷的1/20,得到的结果最差。随着铆测验长度增加,参数等值后的误差均方根减小。但当铆测验长度增加到全卷的1/5以后,等值误差均方根没有明显的减小。在单维IRT中,Harris和Crouse(1993)建议铆测验长度不需要太长,经验的标准是铆测验至少需包含8道题目或者占全卷的20%(Sykes,1997)。在本研究中,对于SL,HB和LS方法,虽然铆测验长度对等值误差均方根的影响在统计检验上达到了显著水平,但是该变量在数值上的影响较为微弱。这与Yao(2011)的研究结果类似,在多维IRT等值中,如果选择了较好的等值方法,等值结果准确性将几乎不受铆测验长度影响。这可能是在数据模拟与模型拟合过程中,均采用了多维补偿性模型的缘故。该结果对于实际应用具有重要的意义,一旦选择了良好的多维IRT等值方法,只需要较少数量的铆题就能得到较准确的等值结果。这样既能够减少编制铆题时花费的人力物力,还能在一定程度上缩短测验长度,提高效率。对于第二个研究问题,不同的铆测验选择方法对SL,HB和LS方法没有显著影响。在构建铆测验时,基本要求是它应当是整个测验的一个“微缩版本”(Kolen&Brennan,2004)。很多研究者关注了铆测验在内容上的代表性(Cook&Petersen,1987)。他们认为,使用具有内容代表性的铆测验能够去除等值偏差,并且增加估计的等值系数的精确性。因此本研究假设,如果按照两个维度题目数量的比例选择铆题,会得到较好的等值结果。研究结果没有证明之前的假设,这其实也没有违背对铆测验内容代表性的要求。因为在研究设计中,每个维度的铆题都符合简单结构。可以推测,如果某些维度不含铆题,或者含有的铆题均同时属于多个维度(项目内多维),那么将会违背铆测验具有内容代表性的原则,从而导致有偏差的等值结果。另外,铆测验选择策略的问题,对于单个维度来说就转化为铆测验长度的问题,只要对于每个维度来说,简单结构的铆题数量达到了一定的比例,就能得到较稳定的等值结果。
最后,在大多数关于多维IRT等值的研究中,都只考察了等值方法对题目参数的返真性(Oshima et al.,2000;Yao&Boughton,2009;Simon,2008)。但是,有些情况下等值的目的是将参加不同测验考生的能力水平调整到同一量尺上。因此,本研究还包括了对各种等值方法下,能力参数返真性的比较。对于SL,HB和LS方法,两个维度能力参数的等值结果普遍受到相关和测验长度的影响。另外,题目数量少的维度能力参数等值结果较差,并且容易受到铆测验长度和等值群体的能力水平差异的影响。说明对于题目数量少的维度,更应该注意对铆测验的选择。总的来说,即使对于这三种方法,能力参数等值后的误差均方根也较大。为了探索原因,以铆测验设计9~11为例(在此情况下测验长度最长,且两个维度的题目数量相等,参数估计准确性应当最高),计算了BMIRT对能力参数估计值的误差均方根。结果显示,SL,HB和LS方法能力参数估计的误差均方根在0.375到0.436之间,而参数的等值误差均方根在0.375到0.439之间。因此,能力参数等值后的误差很可能大部分来源于参数估计的误差。迄今,很多研究者已经对多维IRT模型的参数估计进行了深入的研究(de la Torre,2009;Zhang&Stone,2004;Bolt&Lall,2003;Yao,2003),并编写了一些估计软件。其中大部分能得到较为准确的题目参数估计结果,而能力参数估计结果并不理想。因此,采用合适的估计方法减小模型对能力参数估计的误差,可能是提高多维IRT能力参数等值准确性的一个有效途径。
现在,多维IRT模型在教育测量领域得到了越来越多的应用。多维IRT等值自然也成为了实际中急需实现的方法。本研究探讨了五种常用的多维IRT等值方法在不同铆测验设计下的表现,对多维测验中多维IRT等值方法的选择和铆测验的设计具有一定的实践意义。第一,在编制多维IRT测验时,应尽量保证每个维度都有充足的题目数量,维度之间具有较高的相关。第二,在设计多维IRT等值的铆题时,应当保证每个维度都有一定数量的铆题,并且尽可能使用简单结构的铆题。另外,各维度铆
题的分布不一定需按照全卷各维度题目数量的比例,但需要达到每个维度铆测验长度比例的最低标准。第三,在等值方法上选择使用SL,HB和LS方法,尽量避免MM和MS方法。本研究还存在一定的局限性。如研究数据均模拟0/1计分的题目,并且被试的能力分布也满足多元正态分布,在实际中会出现等级评分的题目甚至混合类型的题目,并且被试群体的能力也会呈现出各种分布形态,有必要在以后的研究中对这些更加复杂的情况加以讨论。此外,研究仅讨论了对于维度能力的等值,实际中可能还需要实现对总能力的等值。因此结合Yao(2011)提出的方法,在各条件下对多维IRT维度能力和总能力等值的结果进行比较,是值得进一步研究的问题。

本研究得到的主要结论如下:
第一,在本研究设置的各个模拟条件下,多维SL,HB和LS等值方法得到的等值结果比MM和MS方法准确,并且这三种方法表现更加稳定。在等值群体的能力水平存在差异的情况下,多维MM和MS等值方法得到的等值结果误差很大。因此,在等值方法选择上,推荐使用多维SL,HB和LS等值方法。
第二,对于多维SL,HB和LS等值方法:(1)测验长度对各参数的等值结果影响显著,测验长度越长,等值结果的误差均方根越小;(2)铆测验长度对各参数的等值结果有一定影响,铆测验长度越长,等值误差均方根越小;(3)铆测验选择策略对各参数等值结果没有显著的影响;(4)维度之间的相关对区分度参数和截距参数的等值结果没有影响,对于能力参数,随着相关的增加等值误差均方根减小;(5)等值群体的能力水平差异仅对截距参数有一定影响,在非等组的条件下得到的等值误差均方根大于等组的条件。
Ackerman,T.A.(1994).Using multidimensionalitem response theory to understand what items and tests are measuring.Applied Measurementin Education,7
(4),255–278.Angoff,W.H.(1982).Summary and derivation of equating methods used at ETS.Test Equating,55
,69.Bolt,D.M.,&Lall,V.F.(2003).Estimation of compensatory and noncompensatory multidimensionalitem response models using Markov chain Monte Carlo.Applied Psychological Measurement,27
(6),395–414.Bradlow,E.T.,Wainer,H.,&Wang,X.H.(1999).A Bayesian random effects model for testlets.Psychometrika,64
(2),153–168.Brossman,B.G.(2010).Observed score and true score equating procedures for multidimensional item response theory.University of Iowa.
Cook,L.L.,&Paterson,N.S.(1987).Problems related to the use of conventional and item response theory equating methodsin lessthan optimalcircumstances.Applied Psychological Measurement,11
(3),225–244.Davey,T.,Oshima,T.C.,& Lee,K.(1996).Linking multidimensional item calibrations.Applied Psychological Measurement,20
(4),405–416.de la Torre,J.,&Song,H.(2009).Simultaneous estimation of overall and domain abilities:A higher-order IRT model approach.Applied PsychologicalMeasurement,33
(8),620–639.DeMars,C.E.(2006).Application of the bi-factor multidimensionalitem response theory modelto test let-based tests.Journal of Educational Measurement,43
(2),145–168.Hanson,B.A.,&Béguin,A.A.(2002).Obtaining a common scale for item response theory item parameters using separate versus concurrent estimation in the common-item equating design.Applied PsychologicalMeasurement,26
(1),3–24.Harris,D.J.,&Crouse,J.D.(1993).A study of criteria used in equating.Applied Measurement in Education,6
(3),195–240.Kim,S.H.,&Cohen,A.S.(1998).A comparison of linking and concurrent calibration under item response theory.Applied Psychological Measurement,22
(2),131–143.Kim,S.H.,&Cohen,A.S.(2002).A comparison of linking and concurrent calibration under the graded response model.Applied Psychological Measurement,26
(1),25–41.Klein,L.W.,&Jarjoura,D.(1985).The importance of content representation for common-item equating with nonrandom groups.JournalofEducationalMeasurement,22
(3),197–206.Kolen,M.J.,&Brennan,R.L.(2004).Test equating,scaling,and linking:Methods and practices.
New York:Springer Verlag.Li,Y.H.,&Lissitz,R.W.(2000).An evaluation of the accuracy of multidimensional IRT linking.Applied Psychological Measurement,24
(2),115–138.Marco,G.L.,Petersen,N.S.,&Stewart,E.E.(1983).A large scale evaluation of linear and curvilinear score equating models Volume I
(RM-83-2).Princeton,NJ:Educational Testing Service.Min,K.S.(2003).The impact of scale dilation on the quality of the linking of multidimensional item response theory calibrations
.Michigan State University,Department of Counseling,Educational Psychology,and Special Education.Oshima,T.C.,Davey,T.C.,& Lee,K.(2000).Multidimensional linking: Four practical approaches.Journal of Educational Measurement,37
(4),357–373.Reckase,M.D.(1985).The difficulty of test items that measure more than one ability.Applied Psychological Measurement,9
(4),401–412.Reckase,M.D.(2009).Multidimensional item response theory.
New York:Springer Verlag.Reckase,M.D.,&Martineau,J.(2004).The vertical scaling of science achievement tests
.Committee on Test Design for K-12 Science Achievement.Washington,DC.Schönemann,P.H.(1966).A generalized solution of the orthogonalProcrustes problem.Psychometrika,31
(1),1–10.Simon,M.K.(2008).Comparison of concurrent and separate multidimensional IRT linking of item parameters
.University of Minnesota.Sinharay,S.,&Holland,P.W.(2007).Is it necessary to make anchor tests mini-versions of the tests being equated or can some restrictions be relaxed.JournalofEducational Measurement,44
(3),249–275.Sykes,R.C.(1997).Guidelines for the selection of anchor items for mixed(or single)item format tests
.Monterey,CA:CTB/McGraw-Hill.Weeks,J.P.(2010).Plink:An R packageforlinking mixed-format tests using IRT-based methods.Journal of Statistical Software,35
(12),1–33.Yao,L.H.(2003).BMIRT:Bayesianmultivariateitem response theory
.Monterey,CA:CTB/McGraw-Hill.Yao,L.H.(2004).LinkMIRT:Linking of multivariate itemresponse model
.Monterey,CA:Defense Manpower Data Center.Yao,L.H.(2011).Multidimensional linking for domain scores and overall scores for nonequivalent groups.Applied Psychological Measurement,35
(1),48–66.Yao,L.H.,&Boughton,K.(2009).Multidimensional linking for tests with mixed item types.Journal of Educational Measurement,46
(2),177–197.Yon,H.(2007).Multidimensionalitem responsetheory(MIRT)approaches to vertical scaling.Michigan State University.
Zhang,B.,&Stone,C.(2004).Direct and indirect estimation of three-parameter compensatory multidimensional item response models
.Paper presented at the annual meeting of the American Educational Research Association,San Diego,CA.
