因变量为等级变量的中介效应分析*

刘红云 骆 方 张 玉 张丹慧

(1北京师范大学心理学院应用实验心理北京市重点实验室;2中国基础教育质量评价与提升协同创新中心;3北京师范大学教育学部,北京 100875)

1 引言

揭示变量间的关系是心理学量化研究的一个重点。中介效应作为变量间复杂作用机制的一种形式,其理论和应用研究在心理学中均占有重要位置。一方面,研究变量间的中介关系可以对变量间的因果作用机制进行验证,丰富心理学理论的内涵;另一方面,根据变量间的中介关系进行干预研究,在组织心理学、工业心理学和临床心理学中都有广泛的应用前景。

近几十年来,中介效应的理论和应用研究备受关注,在连续变量的中介效应模型中,自变量(

X

)、中介变量(

M

)和因变量(

Y

)之间的关系如图1(b)所示。中介模型的含义是指自变量

X

通过对中介变量

M

发生影响,进而影响因变量

Y

。图1(a)中,

c

表示当不考虑中介变量时,

X

对

Y

的影响,

e

是对应的残差;

a

表示

X

对

M

的影响;

b

表示

M

对

Y

的影响;

c

′表示考虑了中介变量

M

后,

X

对

Y

的直接影响;

e

和

e

分别表示

M

变量和

Y

变量的残差。基于图1的模型,Baron和Kenny (1986)所提出的中介效应检验方法和程序至今仍被广泛应用。中介效应大小的计算方法一般有两种。其一是回归系数差异法(Difference of Coefficient),可以通过计算

c-c′

来表明中介效应大小,并常使用Freedman和Schatzkin (1992)的方法进行假设检验。另一种方法为系数乘积法(Product of Coefficient),它是基于路径分析,把中介效应看作是两个回归系数——自变量到中介变量的回归系数(

a

)和中介变量到因变量的偏回归系数(

b

)的乘积,即

ab

。常用的

ab

估计量的检验方法有Sobel检验(Sobel,1982)、Aroian检验(Aroian,1947)和Goodman检验(Goodman,1960)。在没有缺失值的数据中,对于连续变量可以用标准最小二乘回归模型来估计中介效应,系数乘积法和系数差异法的结果是相同的(MacKinnon,Warsi,&Dwyer,1995)。随着结构方程模型以及一系列新的估计方法的发展,中介效应的分析方法不断得以完善,MacKinnon 在改进和完善中介效应的精度和准确性方面做出了很大的贡献(MacKinnon,2008),Baron和Kenny (1986)的方法也在应用中不断完善和发展(方杰,张敏强,2012;温忠麟,张雷,侯杰泰,刘红云,2004;Zhao,Lynch,&Chen,2010;温忠麟,刘红云,侯杰泰,2012)。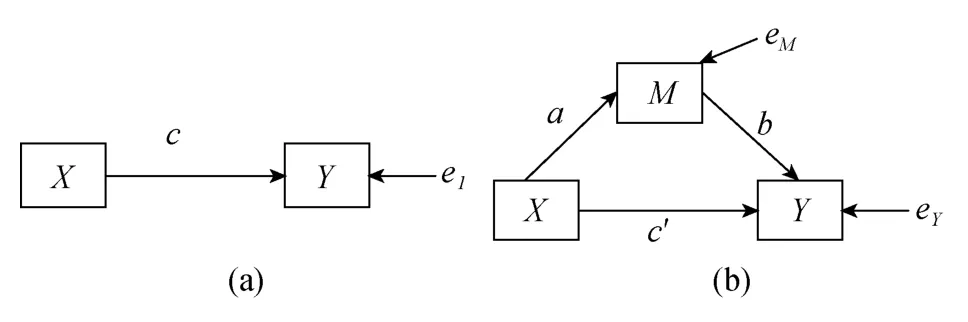

图1 中介模型图示

然而以往的研究大多局限于自变量、中介变量和因变量均为连续变量的情景。对于因变量为分类或等级变量的情景,研究相对较少(Mackinnon,Lockwood,Brown,Wang,&Hoffman,2002)。对于自变量

X

为分类或者等级变量的情景,可以通过定义虚拟变量(Dummy Variable)的方法来处理,中介效应的分析与连续变量的步骤完全相同。但是如果因变量是分类或等级 变量,自变量是连续变量,正确的做法是采用Logistic回归取代通常的线性回归(Nelder &Wedderburn,1972;Pregibon,1981),回归系数的尺度转换为Log量尺。因此对于分类或者等级因变量(

Y

)、连续中介变量(

M

)和自变量(

X

)的中介效应模型,

M

对

X

的回归系数(连续变量的量尺)与

Y

对

M

的回归系数(Logit或Log量尺)和

Y

对

X

的回归系数均不在相同的尺度上,因此不能简单采用处理连续变量中介效应的方式,直接将回归系数

a

和

b

相乘或将

c

和

c’

相减得到中介效应大小。有关二分数据或二分数据与连续数据混合的中介效应分析,研究者提出了一些解决方法。比如,Muthén (1984)通过阈值函数来定义观测分类变量与连续潜变量之间的关系,基于大样本和正态分布的假设,采用广义最小二乘估计法对中介效应进行估计;Winship和Mare (1983)采用阈值的方法,在正态分布和二项分布的假设下构建观测分类变量的概率模型,采用非线性最小二乘估计对中介效应进行估计。这两种方法理论假设太强,需要满足较多的假设条件且对应用者来讲很难操作。MacKinnon和Dwyer (1993)提出了一种切实可行的解决方法,他提出由于不同回归方程得到的系数不可比,在计算中介效应之前应对系数进行方差校正,即标准化,使系数的量尺与标准化的预测变量的单位一致。随后,MacKinnon,Lockwood,Brown,Wang和Hoffman (2007)采用模拟研究的方法比较了系数乘积法和系数差异法的检验结果,发现结果并不相同,有时相差还比较大,推荐使用系数乘积法,同时探讨了系数乘积法的稳健性。Iacobucci (2012)对因变量为分类数据的中介效应进行了探讨,强调在实际应用中研究者应该关注因变量的性质,选择合适的中介效应分析方法。在应用领域上,Li,Schneider和Bennett (2007)对中介变量为二分变量时中介模型做了探讨,结果表明校正后的系数乘积法得到的中介效应估计量比系数差异法得到中介效应估计量精确得多,并提示不应该使用原始未经校正的中介效应估计量。

目前有关中介效应的研究以连续变量为主,一些研究者虽然将其扩展到非连续数据的情境,但此类研究相对较少,且已有的研究主要以二分因变量为主,对多于两个类别的等级变量中介效应尚需进一步的研究。另外,等级数据的中介效应分析是否可以近似将其视为连续数据处理,以及等级数据类别数的多少是否会影响其处理结果等问题尚没有研究进行探讨。一些其他的统计方法,如因素分析,有研究表明如果等级数据的类别数目较少(如少于五个),采用极大似然估计时,估计参数的大小、模型的拟合指标和参数的标准误会产生偏差,随着类别数的增加,偏差减小;但是当等级数增加到四个以上时,稳健的极大似然估计可以得到近似无偏的结果(Muthén &Kaplan,1985;Rhemtulla,Brosseau-Liard,&Savalei,2012)。那么在中介效应的分析中,对于等级数据如果采用连续数据的分析方法会不会随着等级类别数的增加,参数估计会越来越准确呢？为此,本研究拟采用模拟研究的方法,主要解决以下几个问题：(1)对于等级因变量的中介效应模型,考察正确的 Logistic回归分析方法与错误的连续变量回归分析方法的差异;(2)比较系数乘积法和系数差异法的差异;(3)考察等级因变量类别数的变化,是否会影响中介效应分析方法的结果。同时,分析比较样本量以及中介效应大小对参数估计结果以及统计检验的影响。最后通过一个应用实例来说明因变量为等级数据时中介效应的分析及检验过程,以供实际应用者参考。

2 等级因变量的中介效应模型及分析

2.1 二分因变量的中介效应模型

对于图1所示的中介效应模型,针对二分因变量(

Y

)建立Logistic回归方程式：

在连续因变量的中介效应模型中,中介效应大小等于

ab

或

c-c’

。但是,在Logistic回归中介模型中,由于

b

系数是以 logit为单位,与

a

系数不在同一个尺度上,此时中介效应大小并不等于

ab

。同样地,方程(1)和(2)中因变量取值的条件概率不是受同一自变量的影响,回归系数

c

与

c’

的量尺也不同。

不同方程得到的回归系数只有量尺相同,才具有可比性,也才能计算中介效应。按照MacKinnon和Dwyer (1993),MacKinnon (2008)的建议,可以通过标准化转换实现回归系数的等量尺化。转换方法如下：

上述公式中,左边均带有上标 std,表示由logit单位的系数转换而来的标准化系数。利用原始数据可计算

SD (X)

和

SD (M)

,对于

SD (Y')

、

SD (Y")

,可根据MacKinnon (2008)的方法计算：

其中,π/3是标准Logistic分布的方差。将公式(9)～(10)代入公式(6)～(8),可以计算出标准化的回归系数,进而可以用系数乘积法或系数差异法得到中介效应大小,以及中介效应占总效应的比例等信息。

2.2 多类别等级因变量的中介效应模型

在心理学研究中会经常遇到等级数据,比如Likert量表获得的数据就是典型的等级变量。当因变量为多个类别的等级变量时,可以采用累积Logistic模型进行回归分析。

对任一类别

j

,Logit

P

是自变量

X

的线性函数,

α

和

β

为待估参数。累积Logistic回归模型严格遵循成比例发生比(Proportional Odds)假设,即自变量的回归系数

β

与

j

无关(McCullagh,1980)。

本研究把累积 Logistic回归拓展到中介效应的分析过程中,则图1描述的中介效应模型可以表示为：

其中,

X

和

M

为连续变量,方程(14)与方程(3)相同。在方程(12)和(13)中由于

c

,

b

和

c’

不会因为

j

的取值不同而发生变化,所以中介效应的大小并不受因变量等级类别数的影响,而且其标准化方法也与二分因变量的相同。

2.3 等级因变量中介效应的检验和区间估计

标准化回归系数对应的标准误为(MacKinnon,2008)：

3 模拟研究

3.1 模拟设计

模拟研究中考虑的主要因素有：因变量等级数、样本容量、中介效应和分析方法。

(1)因变量等级数：取二类、三类和五类三个水平。二分变量服从二项分布取值为 0-1;三类别和五类别因变量服从多项分布,取值分别为0,1,2和0,1,2,3,4。对于自变量和中介变量,假设其服从标准正态分布。

(2)样本量从小到大依次取 50,100,200,500,1000五个水平。

(3)对中介效应大小,参照 MacKinnon等人(2007)的研究,分别设定标准化回归系数a、b与c′为0,0.14,0.39和0.59四个水平。当三个回归系数均为 0.59时,转换成 logit形式的回归系数是非实数解,因而取消这种组合条件后,对于中介效应的大小总共有63种组合条件。在这些组合条件下,一共产生了7种中介效应值,分别为0,0.0196,0.0546,0.0826,0.1521,0.2301,0.3481。

(4)中介效应的分析方法,包括正确的等级因变量(对于二分变量,采用Logistic回归模型;对于三类别或五类别等级变量,采用累积Logistic模型)和错误的连续变量两种回归分析方法,每种分析方法下又都包含系数乘积法和系数差异两种方法,因而交叉组合后共有4种分析方法。

本模拟实验共生成3×5×63=945组数据,每种条件重复500次。对于每组数据采用4种分析方法计算中介效应。模拟数据的生成和分析均采用Mplus 6.0完成,数据的整理和评价指标计算采用SPSS软件。

3.2 评价指标

评价不同分析方法优劣的指标主要有：中介效应估计的精度(包括中介效应的估计偏差和误差均方根)、中介效应标准误估计的精度、估计中介效应置信区间对真值的覆盖率、统计检验力、一类错误概率等。

4 模拟研究结果

4.1 模型收敛情况

在所有的数据条件下,采用错误的连续数据的方法处理中介效应不存在收敛的问题。采用Logistic回归的收敛比率介于 96.28%～100%之间,大多数条件下的分析全部收敛,只有个别条件下,如样本量很小(样本量为 50),或中介效应很大(如标准化系数b和c′均为0.59)时,存在部分结果不收敛的问题,但是总体来看不收敛比率很低。值得注意的是随着因变量类别数的增多,小样本情况下不收敛的比例有增加的趋势。

4.2 中介效应估计精度

对于每种条件下的数据分别采用4种方法进行中介效应的估计,分别为等级变量的系数乘积法(

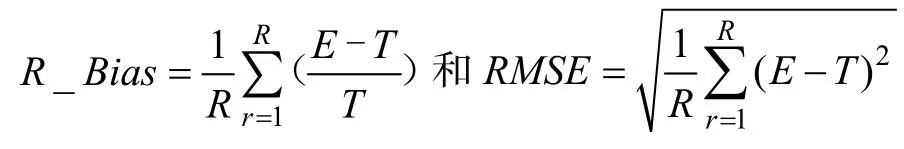
ab

)和系数差异法(

c-c’

)和连续变量的系数乘积法(

ab

)和系数差异法(

c-c′

)。图2(a)-(c)给出了采用不同的估计方法得到的中介效应的相对偏差。由于采用连续变量的回归分析方法,系数乘积法(

ab

)和系数差异法(

c-c′

)得到的结果相同,这里只呈现系数乘积法(

ab

)的结果。图2(a)-(c)显示：中介效应的相对偏差整体上为负,三种方法得到的中介效应均有不同程度的低估,但是使用正确方法得到的相对偏差较小。如对二分因变量的数据,三种方法之间差异最大,使用Logistic回归估计中介效应

ab

的相对偏差最小(接近于零),其次是系数差异法(

c-c’

)的相对偏差,而使用连续因变量回归得到中介效应

ab

的相对偏差最大。三种估计方法之间的差异随着因变量类别数的增加而减小,当因变量增大到五个类别时,三种方法之间的差异已经很小。估计相对偏差随着中介效应的增大而增大,样本量的大小对中介效应估计相对偏差的影响不大。中介效应估计的误差均方根的结果表明,对于二分类的数据和三分类的数据,到的中介效应

ab

的精度相对较低。图2(d)-(f)给出了不同方法中介效应估计的误差均方根与中介效应大小的关系。可以看出,三种方法随着中介效应的增大误差均方根均有增大的趋势,对于二分类的因变量,中介效应较小时,

ab

和

ab

之间的差异较小,但是随着中介效应的增大,连续数据的处理方法

ab

得到的中介效应估计的误差均方根明显大于等级变量的系数差异法(

ab

)的结果;同时,在任何情况下系数差异法得到的结果都比系数乘积法得到的结果略差。此外,图2 (f)所示的不同方法的误差均方根均比图(d)和(e)中相应的该方法下的结使用 Logistic回归估计中介效应

ab

的精度最高,而系数差异法(

c-c’

)和使用连续因变量回归得果要小,说明中介效应估计的精度受因变量类别数影响,因变量的类别数越多,参数估计精度越高。图2 (f)还显示,当因变量的类别数达到五个时,连续数据分析方法的误差均方根与等级数据分析方法的结果已经非常接近了。

图2 不同方法中介效应估计的偏差和误差均方根与中介效应大小的关系

中介效应估计的相对偏差随样本量的增大,没有明显的变化趋势。中介效应估计的误差均方根随着样本量的增大有明显的减小趋势(表1),在样本量较小时,即使采用了正确的等级数据的分析方法,中介效应估计的误差均方根仍然较大,在样本量小于 200的情况下,出现了比错误的连续数据处理方法得到的误差还要略大的情况。可见,对于等级数据,要想得到较为准确的参数估计结果,对样本量的要求更高,当样本量高于200时,等级数据的分析方法得到的中介效应的估计精度要高于连续数据,尤其是对于二分因变量的结果。

表1 中介效应估计的误差均方根与样本量的关系

4.3 中介效应标准误估计的精度

中介效应估计值的标准误对中介效应的检验和区间估计非常重要,这里采用相对偏差描述标准误估计的精度。即对每种条件下,分别计算500个中介效应估计值的标准差(将其看做标准误的真值,记为

T

)和500个中介效应估计值对应的标准误的均值(

M

),则标准误对应的相对偏差为：

(M-T)/T

。附表1给出了中介效应估计值标准误的相对偏差,从附表1可以看出,在各种条件下,无论采用分类数据的 Logistic回归还是通常的线性回归,系数乘积法的对应的相对偏差远远小于系数差异法,而且系数差异法对应的相对偏差在所有条件下均小于零,说明低估了中介效应的标准误。另外,对于系数乘积法,在各种条件下,两种回归的中介效应标准误估计偏差相当接近,并且绝对值都不超过0.05,说明对于系数乘积法,中介效应标准误估计的偏差不大。

4.4 中介效应置信区间对真值的覆盖率

应用正态分布理论,通过估计值±1.96×估计标准误来构建 95%的置信区间,每一种条件下的 500次重复中置信区间包含真值的比例,称作中介效应置信区间对真值的覆盖率(CI Recovery Rate)。覆盖率的大小可以从一定程度上反映估计中介效应的准确性。附表2给出了不同方法中介效应置信区间对真值的覆盖率。结果表明,对于正确的等级数据的分析方法,在绝大多数条件下,系数乘积法

ab

得到的置信区间对真值的覆盖率均接近95%,且这一覆盖率不受中介效应大小、样本量大小和因变量类别数的影响,是最优的分析方法;而对于等级数据系数差异法

c-c’

得到的置信区间的覆盖率在70%左右,每种情况下均显著低于系数乘积法,结合标准误的估计精度,系数差异法覆盖率低与标准误被低估有关。因变量类别数较少时,系数乘积法

ab

得到的真值覆盖率显著低于等级数据系数乘积法

ab

的结果,但是随着因变量类别数的增加,

ab

法得到的覆盖率越来越接近95%。因此,就中介效应置信区间对真值的覆盖率来看,

ab

方法应是首选,另外与前面中介效应估计精度的结果一致,随着因变量类别数的增加,采用连续变量回归的系数乘积法与正确Logistic回归的标准化系数乘积法差异越来越小。

4.5 统计检验力

中介效应的统计检验力(Power)反映了中介效应的真值不为0时,其估计值也显著不等于0的概率。每种条件下的500次重复中,对于0.05的显著性水平,得到检验结果显著的比例称作该条件的统计检验力。附表3给出了中介效应统计检验力的估计结果。从检验力的结果可以看出随着中介效应的增大和样本量的增加,等级数据分析方法和连续数据分析方法的检验力都随之增大,且中介效应

ab

和中介效应

ab

的统计检验力差异不大,但在系数差异法的估计结果上,连续数据分析方法(

c-c’

)的检验力要略高于等级数据分析方法(

c-c’

),尤其是在中介效应较小或样本量较小的情况下,两者差异略大。相对于系数乘积法,系数差异法的检验力略高,可能是因为系数差异法低估了标准误而导致的。另外,随着因变量类别数的增加,中介效应的统计检验力有增大的趋势,但变化趋势不太明显。值得注意的是,统计检验力差异不大并不能说明两种方法没有差异,这可能是因为错误使用连续数据的处理方法后,中介效应值和标准误均被低估而导致的(结合参数估计精度部分和标准误估计精度的结果)。

4.6 第Ⅰ类错误

当中介效应的真值为0时,如果估计得到的中介效应显著不等于 0,那么在统计上是犯了第Ⅰ类错误(Type Ⅰ Error)。在500次重复条件中,发生第Ⅰ类错误所占的比例称作第Ⅰ类错误率。在本研究中,中介效应的真值等于 0的情况分为三种：(1)a=b=0;(2) a=0,b≠0;(3) a≠0,b=0。附表4 给出了不同分析方法下中介效应第Ⅰ类错误率的比较结果。对于0.05的显著性水平,整体来看,等级数据分析方法和连续数据分析方法,系数乘积法得到的中介效应第Ⅰ类错误率分别为0.01270和0.01299,两者差异不大,且都不超过 0.05;系数差异法得到的中介效应第Ⅰ类错误率分别为0.11310和0.14530,说明系数差异法犯第Ⅰ类错误的概率较大,这与前面的系数差异法低估标准误的结论一致。每种条件下,系数乘积法所犯的第Ⅰ类错误率都明显小于系数差异法;其次,在不同的样本量条件下,同是系数乘积法计算得到的中介效应,使用 Logistic回归所犯的第Ⅰ类错误率与使用连续变量回归所犯的第Ⅰ类错误率相差很小;对于系数差异法得到的中介效应的第Ⅰ类错误率,等级数据的分析方法小于连续数据分析方法。对于a、b同时等于0的情况,不同方法所犯第Ⅰ类错误率均低于a、b不同时等于0的情况,当 a=0,b≠0时,系数差异法所犯第Ⅰ类错误率最大。

5 等级因变量中介效应分析步骤与应用

下面通过一个实际应用的例子来源于：Anderson,R.E.,Hair,J.F.,Tatham,R.L.,&Black,W.C.(2006). :Pearson.P28-31.,说明因变量为等级变量时中介效应的分析步骤。

研究问题：采用消费心理学中关于100名顾客购买行为所受影响因素研究的数据,研究者要求被试填写对 HBAT公司产品的质量和对商家服务满意度的评定量表,并随后记录了被试是否购买了该商家的产品。研究目的是探讨顾客的购买行为(

Y

)、产品质量(

X

)和顾客对商家满意度(

M

)之间的关系。本研究中假设

Y

为因变量,

X

为自变量,

M

为中介变量,其中顾客的购买行为

Y

为二分变量,1表示购买,0表示不购买。

X

和

M

为连续变量。

第一步：回归分析

这一步需要做以下三个回归：

(1)做因变量

Y

对自变量

X

的Logistic回归,得到

c

的估计值以及对应的标准误

SEc

的估计值。本例中计算得到

c

=1.058,

SEc

=0.217。(2)做因变量为

M

,自变量为

X

的线性回归,得到

a

的估计值以及对应的标准误

SEa

。本例计算得到

a

=0.415,

SEa

=0.075。(3)做因变量

Y

对自变量

X

和

M

的Logistic回归,得到

b

和

c'

的估计值以及对应的标准误。本例计算得到

b

=0.959,

Seb

=0.283;

c'

=0.755,

SEc'

=0.221。

第二步：标准化

这一步需要将第一步计算得到的回归系数通过标准化的方法转换到统一的量尺上。

(1)计算

X

、

M

、

Y'

和

Y"

的标准差、方差以及

X

和

M

的协方差,在本例中

SD

(

X

)=1.396

SD

(

M

)=1.192,

Var

(

X

)=1.950,

Var

(

M

)=1.420,

Cov

(

X

,

M

)=0.809。分别用公式(9)和(10)计算

Y'

和

Y"

的方差。

V ar

(

Y

')=5.473,

Var

(

Y

'')=6.879,

Y'

和

Y"

的标准差分别为2.339和2.623。(2)分别用公式(6)～(8)对回归系数标准化。标准化的回归系数分别为：

b

=0.436,

c

=0.631,

c

=0.402。

本研究的结果显示系数乘积法(

ab

)是最优的,推荐使用系数乘积法的估计结果。

中介效应对应的标准误为：

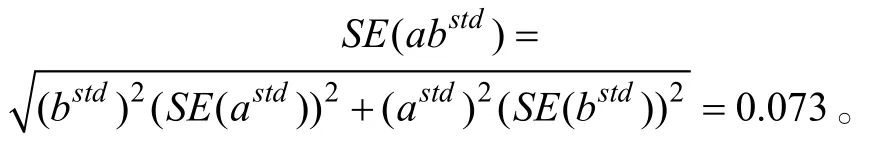
以上第一步可以通过SPSS或SAS软件做回归得到,第二步和第三步可以通过简单计算得到。另外,Mplus软件可以直接得到标准化后的系数及标准误估计,附录中给出Mplus的语句。关于中介效应更多的应用程序和资料可以参考Hayes (2013)的介绍。

6 讨论

若中介模型中的因变量是等级数据,则应使用等级因变量的 Logistic回归来估计中介效应;如果错误地使用连续因变量的线性回归方法,会导致明显低估的中介效应,低估的标准误结果和不正确的置信区间估计等问题。对于等级因变量,可以采用Logistic回归估计得到回归系数,再通过对回归系数标准化实现回归系数尺度的统一和具有可比性。

本研究比较了系数乘积法和系数差异法的差异,无论是正确的等级数据分析方法还是错误的使用连续数据分析方法,均表现为较一致的趋势,即在各个统计检验指标上,包括中介效应置信区间对真值的覆盖率和第Ⅰ类错误率,不同条件下的系数乘积法总是优于系数差异法,这与因变量为连续变量时的研究结果相一致(MacKinnon等人,2002)。造成这个结果的原因在于两种表示中介效应方法的标准误的计算不同,从更深层的原因来说,系数差异法的标准误计算未能充分地、直接地考虑中介变量对因变量的影响,计算得到的标准误出现低估,正是由于这一点,系数差异法的标准误比乘积法的标准误小,检验力出现虚假的偏高。系数乘积法可以得到更加准确的参数估计结果和标准误估计值,同时,所犯第Ⅰ类错误的概率也比系数差异法小。从研究结果还可以看出,Logistic回归的系数乘积法得到的中介效应置信区间对真值的覆盖率始终在95%左右,表现出了比系数差异法非常明显的优势,这一结论与MacKinnon (2008)的研究一致。另外,详细考察不同条件下的检验力和第Ⅰ类错误率的结果发现,系数差异法对中介效应检验的显著性可能更偏向于中介变量和因变量之间的关系,即对于同样大小的中介效应ab值,b值增大可能会得到更强的检验力,以及增大第Ⅰ类错误率,而系数乘积法没有这样的趋势。如对于三类别等级因变量,中介效应为0.0826的情况可以是a=0.14,b=0.59的组合,也可以是 a=0.59,b=0.14的组合,对于样本量为500的情况,两种组合情况下系数差异法的检验力分别为0.93和0.50,显然系数b大时,检验力更大;同样,a=0而b≠0时所犯的第Ⅰ类错误率始终大于b=0而a≠0时的第Ⅰ类错误率,且随着类别数增加,这种趋势更加明显。这一研究结果也与MacKinnon等人(2002)得到的连续变量的结果一致。对于等级因变量的中介效应分析方法的选择,根据本研究的结果推荐使用正确的 Logistic回归得到的结果,对于中介效应的估计建议采用系数乘积法。

当因变量的类别数增加时,连续数据分析方法的估计结果与等级数据分析方法的结果越发接近,也就是说,当类别数增加到一定程度,连续数据分析方法带来的偏差很小。在本研究中,当因变量类别数增大到五类别时,采用系数乘积法时,中介效应置信区间对真值的覆盖率上,等级数据分析方法和连续数据分析方法的结果分别是 95%与 93%左右;第 I类错误率均在 0.014左右。如果因变量类别数从五类别继续增加,可以预计连续数据分析的结果能够达到可接受的水平。这主要是因为等级变量随着类别数的增加越来越接近于连续数据,也就越来越近似满足连续回归分析的假设。但是,虽然本研究的结果表明当等级变量的类别数增大到5及以上时,可以采用连续变量的分析方法进行中介效应分析,在实际应用中仍然需要结合具体的研究问题进行回归方法的选择,并对结果做出合理的有意义的解释(Rucker,Preacher,Tormala,&Petty,2011)。比如,对累积Logistic回归结果的解释可以和不同类别的发生比联系起来,而连续数据的处理方法就无法提供这一方面信息,因而如果研究者关注自变量对因变量发生等级类别的变化的影响,则需要采用累积Logistic回归的方法。

在小样本情况中,等级数据分析方法会变得难以收敛,尤其是在中介效应较大时;同时,在大样本情况下,等级数据处理方法的优势相对比较明显。这些结果表明,对于等级因变量,要得到稳定的参数估计结果,可能需要比连续数据更大的样本量。比如样本量大于200时,才有可能得到相对精确的、比连续数据方法更有效的参数估计结果。

最后,从中介效应检验的角度来考虑,应该对中介效应及其标准误进行标准化。标准化方法有完全标准化和部分标准化之分,在不同软件中计算方法稍有不同,如果采用SPSS和SAS需要自己做一些计算,或者可以应用 Hayes提供的语句(http://www.afhayes.com/)。在 Mplus软件中,采用完全标准化(STDYX)程序可以直接得到标准化的结果,应用起来比较方便,并且很容易推广到多个自变量、中介变量和多个因变量以及潜变量的情景。

7 局限性与展望

此外,本研究只考虑了因变量是等级数据的中介效应分析,当自变量和中介变量是等级数据时的中介效应并没有展开分析和讨论。实际上,如果自变量是等级数据,可以转换成虚拟变量,再采用传统的回归分析就可以进行中介效应分析。如果中介变量是等级变量,可以进行中介变量对自变量的Logistic回归分析(参数估计以及标准化的方法与本文中进行因变量对中介变量的Logistic回归的方法相同),以及把中介变量转换成虚拟变量后,进行因变量对自变量和中介变量的传统回归分析,再采用系数乘积法或者系数差异法估计中介效应的大小以及进行假设检验或者区间估计。研究者在实际应用中应该首先考察自变量、中介变量和因变量的性质,选择合适的回归模型进行中介效应分析。

8 研究结论

本研究可以得出以下结论：

(1)如果中介模型的因变量是二分类或者是多类别的等级变量,应该使用Logistic回归分析方法;如果使用了连续数据分析方法,将会得到有偏的结果,会造成中介效应估计值精度偏低、中介效应置信区间对真值覆盖率偏低、低估标准误等问题。

(2)对于等级因变量的中介效应估计,系数乘积法得到的结果和系数差异法存在差异,系数乘积法的结果更为准确。

(3)当因变量的类别数较多(5及以上)时,可以考虑使用连续数据分析方法,这时需要结合中介效应大小、样本量等情况来分析使用某一种数据分析方法的利弊。

Aroian,L.A.(1947).The probability function of the product of two normally distributed variables.

Annals of Mathematical Statistics,18

,265–271.Baron,R.M.,&Kenny,D.A.(1986).The moderator-mediator variable distinction in social psychological research:Conceptual,strategic,and statistical considerations.

Journal of Personality and Social Psychology,51

(6),1173–1182.Fang,J.,Zhang,M.Q.,&Qiu,H.Z.(2012).Mediation analysis and effect size measurement:Retrospect and prospect.

Psychological Development and Education,28

(1),105–111.

[方杰,张敏强,邱皓政.(2012).中介效应的检验方法和效果量测量:回顾与展望.心理发展与教育,28(1),105–111.]

Fang,J.,&Zhang,M.Q.(2012).Assessing point and interval estimation for the mediating effect:Distribution of the product,nonparametric Bootstrap and Markov Chain Monte Carlo methods.

Acta Psychologica Sinica,44

(10),1408–1420.

[方杰,张敏强.(2012).中介效应的点估计和区间估计:乘积分布法、非参数 Bootstrap和 MCMC法.心理学报,44(10),1408–1420.]

Freedman,L.S.,&Schatzkin,A.(1992).Sample size for studying intermediate endpoints within intervention trails or observational studies.

American Journal of Epidemiology,136

,1148–1159.Goodman,L.A.(1960).On the exact variance of products.

Journal of the American Statistical Association,55

,708–713.Hayes,A.F.(2013).

Introduction to mediation,moderation,and conditional process analysis:A regression-based approach.

New York:Guilford Press.Iacobucci,D.(2012).Mediation analysis and categorical variables:The final frontier.

Journal of Consumer Psychology,22

,582–594.Li,Y.,Schneider,J.A.,&Bennett,D.A.(2007).Estimation of the mediation effect with a binary mediator.

Statistics in Medicine,26

,3398–3414.MacKinnon,D.P.(2008).

Introduction to statistical mediation analysis.

New York:London Lawrence Erlbaum Associates.MacKinnon,D.P.,&Dwyer,J.H.(1993).Estimating mediated effects in prevention studies.

Evaluation Review,17

,144–158.MacKinnon,D.P.,Lockwood,C.M.,Brown,C.H.,Wang W.,&Hoffman,J.M.(2007).The intermediate endpoint effect in logistic and probit regression.

Clinical Trials,4

,499–513.MacKinnon,D.P.,Lockwood,C.M.,Hoffman,J.M.,West,S.G.,&Sheets,V.(2002).A comparison of methods to test mediation and other intervening variable effects.

Psychological Methods,7

(1),83–104.MacKinnon,D.P.,Warsi,G.,&Dwyer,J.H.(1995).A simulation study of mediated effect measures.

Multivariate Behavioral Research,

30,41–62.McCullagh,P.(1980).Regression models for ordinal data(with discussion).

Journal of the Royal Statistical Society.Series B,42

(2),109–142.Muthén,B.(1984).A general structural equation model with dichotomous,ordered categorical,and continuous latent variable indicators.

Psychometrika,49

,115–132.Muthén,B.,&Kaplan,D.(1985).A comparison of some methodologies for the factor analysis of non-normal Likert variables.

British Journal of Mathematical and Statistical Psychology,38

,171–189.Nelder,J.A.,&Wedderburn,R.W.M.(1972).Generalized linear models.

Journal of the Royal Statistical Society.Series A,135

,370–384.Preacher,K.J.,&Kelley,K.(2011).Effect size measures for mediation models:Quantitative strategies for communicating indirect effects.

Psychological Methods,16

,93–115.Pregibon,D.(1981).Logistic regression diagnostics.

The Annals of Statistics,9

,705–724.Rhemtulla,M.,Brosseau-Liard,P.É.,&Savalei,V.(2012).When can categorical variables be treated as continuous? A comparison of robust continuous and categorical SEM estimation methods under suboptimal conditions.

Psychological Methods,17

,354–373.Rucker,D.D.,Preacher,K.J.,Tormala,Z.L.,&Petty,R.E.(2011).Mediation analysis in social psychology:Current practices and new recommendations.

Social and Personality Psychology Compass,5

(6),359–371.Sobel,M.E.(1982).Asymptotic confidence intervals for indirect effects in structural equation models

.

In S.Leinhardt (Ed.),

Sociological methodology

(pp.290–312).Washington,DC:American Sociological Association.Wen,Z.L.,Chang,L.,Hau,K.T.,&Liu,H.Y.(2004).Testing and application of the mediating effects.

Acta Psychologica Sinica,36

(5),614–620.

[温忠麟,张雷,侯杰泰,刘红云.(2004).中介效应检验程序及其应用.心理学报,36(5),614–620.]

Wen,Z.L.,Liu,H.Y.,&Hau,K.T.(2012).

Analysis of moderating and mediating effects.

Beijing,China:Educational Science Publishing House.

[温忠麟,刘红云,侯杰泰.(2012).调节效应和中介效应分析.北京:教育科学出版社.]

Winship,C.,&Mare,R.D.(1983).Structural equations and path analysis for discrete data.

American Journal of Sociology,89

,54–110.Yuan,Y.,&MacKinnon,D.P.(2009).Bayesian Mediation Analysis.

Psychological Method

s

,14

(4),301–322.Zhao,X.S.,Lynch,J.G.,Jr.,&Chen,Q.M.(2010).Reconsidering Baron and Kenny:Myths and truths about mediation analysis.

Journal of Consumer Research,37

,197–206.

附录：因变量为等级变量的中介效应分析Mplus语句

TITLE:this is an example of a Mediation in Categorical Data Analysis

DATA:FILE IS data.dat;

VARIABLE:NAMES ARE id x m y;

CATEGORICAL ARE y;

ANALYSIS:

ESTIMATOR=ML;

MODEL:y on x m;

m on x;

OUTPUT:standardized;

附表1 中介效应估计值的标准误相对偏差

附表2 中介效应置信区间对真值的覆盖比例(%)

附表3 中介效应的检验力

附表4 中介效应第Ⅰ类错误率