现代农业科技园区竞争力评价指标体系研究

潘启龙，刘合光

(1.贵州省人民政府 金融工作办公室，贵阳550004;2.中国农业科学院 农业经济与发展研究所，北京100081)

0 引言

竞争力是指双方或多方参与比较时体现出来的优势能力。经济领域的竞争力比较可以在产品之间、企业之间、产业之间、区域之间以及国家之间等进行。产业园区是指具有一定空间范围的、承载诸多企业及其经营活动的、具备产业发展需要的基础设施和公共服务的特殊区域。显然，产业园区之间可以进行竞争力的比较。

现代农业是指广泛应用现代科学技术、现代工业提供的生产资料和设施装备以及现代科学管理方法的社会化农业［1］。由于具有土地集约性、科技示范性、效益扩散性、区域带动性等优势和特点，现代农业的园区化发展是一种必然趋势，是“以工业的方式发展农业”的重要手段［2］。在我国，各类现代农业科技园区纷纷涌现，为推动现代农业发展作出了重要贡献，与现代农业园区相关的研究也较多，例如，张长海(2012)提出了集科技创新、生产示范、技术推广、科普教育、观光旅游、商业贸易“六位一体”的农业科研单位建设现代农业科技园区的综合发展新模式［3］;董理(2012)提出了从整体规划、发展模式、财政支持、人才培养等方面给予现代农业园区政策支持［4］;周成等(2012)在领导管理体制、运行机制、政策系统及技术、资金、土地、税收、人才体系等方面探索农业科技园区的配套以及保障体系建设［5］;雷广海等(2008)提出了解决农业园区用地的基本思路，构建了园区用地的体系［6］;田逢军(2007)对现代观光农业园区的发展意义、类型及特点、发展模式、开发措施等进行了深入分析［7］。

构建合理的指标体系，对现代农业科技园区进行评价和比较，有助于园区规范化发展和实行标杆管理。通过文献检索发现，我国对现代农业科技园区的综合评价指标体系研究不少，包括期刊文章和学位论文共有20余篇。例如，翟虎渠等(2003)将现代农业科技示范园区的评价体系分为基础设施、技术水平、经济效益、生态效益和组织管理五大一级指标［8］;王欧、吴文良(2003)将现代农业科技园区的综合评价指标分为宏观评价指标、基础条件与生态环境评价指标、效果评价指标、龙头企业评价指标4个大类［9］。钟甫宁、孙江明(2007)将农业科技示范园区评价指标分为建设基础、内部效益、外部效益3 个大类［10］。

但是，除综合评价之外，现有文献在现代农业科技园区的竞争力评价方面的研究则没有。综合评价和竞争力评价具有明显的差别，前者强调的是当前功能和效益评价，后者强调的是持续发展能力评价，在指标体系和各自权重上有较大差别，因此，开展现代农业科技园区竞争力评价指标体系研究十分必要。

依托有关课题，作者对现代农业科技园区竞争力评价问题进行了深入的访谈和问卷调查，取得了第一手资料和数据。本研究即主要根据课题的研究，对现代农业科技园区的竞争力评价指标体系展开论述。另外，在现代农业相关园区的称谓上，不同文献有“现代农业科技园区”、“现代农业示范园区”、“现代农业高新技术产业园区”等不同称谓，但其本质基本相同，本研究统一为“现代农业科技园区”。

1 竞争力分析

1.1 竞争力分析框架

针对不同比较对象，竞争力的分析框架主要包括SWOT分析、波特五力竞争模型、结构-行为-绩效理论、钻石模型等。

SWOT分析主要通过内部优势(strengths)和劣势(weaknesses)、外部机遇(opportunities)和挑战(threats)的比较来确定被分析对象的竞争力，并据此对竞争战略加以调整，以保障被分析对象战略目标的实现［11］。SWOT分析主要用于企业竞争力的战略诊断，也可用于产品、区域、产业等比较分析。

五力竞争模型由迈克尔·波特(Michael Porter)在20世纪80年代初提出，主要用于企业竞争战略分析。所说的五力分别是供应商讨价还价的能力、客户讨价还价的能力、潜在竞争者进入的能力、替代品的替代能力、业内竞争者的竞争能力。这5种力量的消涨变化，决定了企业盈利能力和竞争能力的变化［12］。五力竞争模型也可用于小行业分析。

结构-行为-绩效理论把产业分解成特定的市场，认为市场结构(structure)决定了企业行为(conduct)，而企业行为又决定了市场运行的经济绩效(performance)［13］。该理论也称为SCP分析框架，主要用于分析产业的集中程度和竞争力，是结构主义的代表理论之一。

钻石模型又称钻石理论或国家竞争优势理论，是迈克尔.波特于1990年提出的又一个重要的竞争力理论，主要用于分析一个国家如何形成整体竞争优势。钻石模型构造了国家竞争优势的4个基本要素和2个辅助要素，前者包括生产要素、需求条件、相关产业和支持产业、企业微观个体，后者包括机会、政府两个变数［14］。钻石模型也可应用于区域的竞争分析。

产业园区是产业的空间集合体，产业园区的竞争力分析理应包含园区(区域)和产业两个大的方面。因此，产业园区的竞争力分析往往会综合运用SWOT分析、五力竞争模型、SCP分析、钻石模型等工具，并将其中的一些比较要素抽象出来，形成独特的分析框架。

现代农业科技园区中的产业、区域都具有自身特点，其分析的要素也会有所不同。本研究在参考现代农业科技园区综合评价等有关文献的基础上，综合考虑SWOT分析、五力竞争模型、SCP分析、钻石模型等工具的要素，形成了初步的分析框架和访谈提纲。此后，通过与中国农科院、中国农业大学以及陕西杨凌农业高新技术产业示范区、北京昌平国家农业科技园区等单位有关专家和管理人员进行访谈，最终确定了现代农业科技园区的竞争力分析框架。

1.2 现代农业科技园区的竞争力要素

根据访谈结果，现代农业科技园区的竞争力主要体现在基础建设和园区规模、区位优势和市场环境、产业链条和企业发展、科技创新和人力资本、园区管理和公共服务、政府扶持和政策优惠6个方面。

1.2.1 基础建设和园区规模。基础建设是科技园区吸引投资、持续发展的必要条件，构成了竞争力的重要内容。对于现代农业科技园区来说，道路通信设施、能源水利设施、环保设施以及教科文卫等辅助性设施的功能完备和便利易得，有助于增强自身的竞争优势。

规模对于现代农业科技园区也很重要，规模越大，园区的经济发展越能够自成体系，内生效益越强，竞争力也就越强。评价园区的规模可以从占地面积、园区人口总数、园区建设总投资等角度予以考察。

1.2.2 区位优势和市场环境。区位优势对于现代农业科技园区的竞争力十分重要，主要表现在隶属发达经济圈层、毗邻较多的大中城市、资源丰富、气候适宜、生态环境优良等方面。

优秀的市场环境显然有助于提升现代农业科技园区的竞争力，主要体现在生产要素供应充沛、辐射的消费人群庞大、消费结构多样化等方面。

1.2.3 产业链条和企业发展。现代农业科技园区如果能够推动产业集群发展，形成基础产业、主导产业、高新技术产业、关联和支持产业相互促进、相得益彰的局面，显然会增强自身的竞争力。完善的产业链、严密的产供销系统将使园区经济活力大为增加，形成内生效益。

在企业发展方面，可以用园区企业总数、大中型企业数量、龙头企业带动作用、年度企业增加数量等定量和定性指标加以描述，良好的企业发展状况必然有助于增强园区的竞争力。

1.2.4 科技创新和人力资本。科技创新是现代农业科技园区的发展潜力所在，没有科技创新，科技园区也就失去了存在的价值。科技创新可以从年度研发经费占GDP的比例、年度专利核准数量、科研人员占就业人员总数的比例、科技平台共享和科研院所高校合作情况、年度科研获奖数量等方面加以考察。

人力资本是产业发展、科技创新的基础，也是现代农业科技园区的一个核心竞争力要素。主要可以从认定的高级人才数量、引进的高级人才数量、年度就业人员人均继续教育和培训经费支出等方面予以考察。

1.2.5 园区管理和公共服务。良好的管理是构成现代农业科技园区竞争力的重要因素，主要可以从园区领导机制、管委会工作成效、园区品牌建设、大型活动举办推广等方面加以考察。

良好的公共服务是科技园区吸引企业、推动产业发展的重要手段，可以从审批环节的高效有序、办事流程的简化方便、重点项目的跟踪服务、教科文卫配套服务的优质高效、休闲娱乐服务的丰富易得等方面予以考察。

1.2.6 政府扶持和政策优惠。强有力的政府扶持是形成现代农业科技园区竞争力的重要因素，可以从园区级别(如国家级、省市级)、年度上级政府财政拨付金额、年度企业补贴和奖励金额等方面加以考察。

优惠政策是园区招商引资、外部企业入驻、自主创业等重要的参照指标，主要可以从税费减免措施、融资政策优惠、土地开发政策优惠、投资环境改善等方面加以考察。

2 竞争力评价指标体系

2.1 指标体系的构建

2.1.1 指标选取原则。本研究在指标选取时遵循的主要原则有3个。

一是系统性原则。竞争力评价是一个全面、系统的工作，指标的构建必须考虑涉及现代农业科技园区竞争力的各个方面，不应有疏漏和缺失。

二是客观性原则。现代农业科技园区竞争力指标必须具备较强的客观性，能够将具体园区的竞争力真实地反映出来，而且在进行评价时，评价者能够比较容易地结合指标给出自己的打分，不会造成明显的主观臆断和偏差。

三是逻辑性原则。现代农业科技园区竞争力评价指标应该具有较强的逻辑性，能够科学地反映构成园区竞争力的要素之间联系，同时，各个指标之间要相互区隔，尽量避免明显的包容关系。

2.1.2 层级设计和指标体系。指标体系的构建方法有多种，比较常见的包括主成分分析法、层次分析法、德尔菲法等，本研究从定量分析和定性判断相结合出发，主要应用层次分析法构建指标体系。层次分析法一般将指标体系分解成目标、准则、方案3个层次。

目标层是现代农业科技园区竞争力，准则层包括现代农业科技园区6个方面的竞争力要素，方案层需要依据指标选取原则进行筛选。综合有关访谈结果，经过精心选取和设计，形成了如下的现代农业科技园区竞争力评价指标体系(表1)。

2.2 指标权重的确定

调查问卷中，要求专家对6个准则层指标、单个准则层下属的方案层指标之间的两两重要性进行打分，得到量化定义表(表2)。

依据表2的量化定义，可以对比较的指标组进行重要性两两对比打分。例如，如果指标i比指标j明显重要，则判断系数aij=Wi/Wj=5;反之，如果要素j比要素i明显不重要，则aji=Wj/Wi=1/5。同时，一旦认定指标i对指标j重要性比值，则指标j对指标i重要性的比值为前者的倒数，二者的量化定义具有同一性。

根据层次分析法，在对同级指标的重要性形成判断之后，利用所得数据构造判断矩阵，并通过一致性验证，即可以确定指标体系的权重。课题共发放问卷30份，回收有效问卷29份，符合层次分析法的样本要求，取得了指标权重的基础数据，进而对现代农业科技园区竞争力评价指标体系的权重进行计算和确定。

2.2.1 准则层指标权重。对29份有效问卷进行汇总，对每一个指标相对重要性的数据相加，再求以均值，以此构成相关权重的判断矩阵。

对于准则层指标，问卷得到的相对重要性两两比较的数据见表3。

以表3的数据构成一个6×6的矩阵，用方根法进行归一化处理，得出6个准则层指标的权重分别为:0.162 6，0.172 3，0.170 4，0.164 7，0.158 3，0.171 6。同时，求得该矩阵的最大特征值λmax=6.001 6，一致性指标 CI=(λ -n)/(n-1)=0.000 3，查表得与n=6对应的随机一致性指标RI=1.255，则一致性检验系数CR=CI/RI=0.000 2。CR≤0.1时，指标权重为有效，因此通过一致性检验。

表1 现代农业科技园区竞争力评价指标体系Tab.1 Competitiveness evaluating criterion system for modern agricultural science-technology area

表2 量化定义表Tab.2 Quantitative definition list

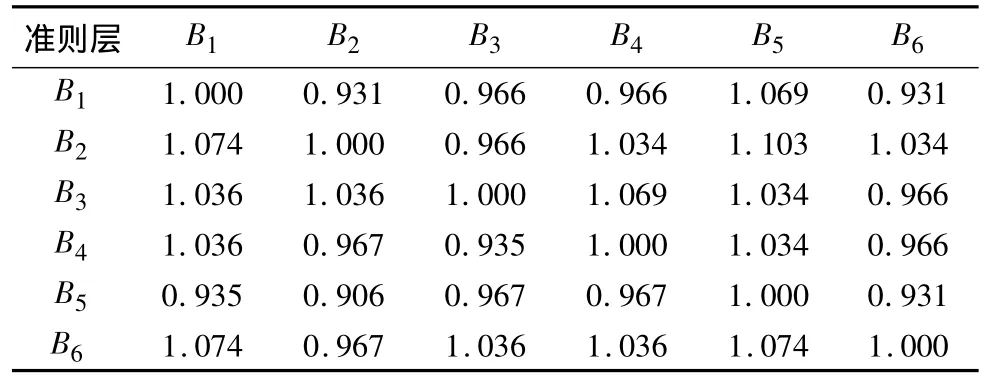
表3 准则层权重判断数据表Tab.3 The table of rule layer’s weights judgment data

2.2.2 B1的方案层指标权重。对于B1的方案层指标，问卷得到的相对重要性两两比较数据见表4。

以表4的数据构成一个7×7的矩阵，用方根法进行归一化处理，得出B1的7个方案层指标权重分别为:0.147 8，0.146 1，0.136 6，0.135 0，0.141 2，0.137 3，0.155 9。同时，求得该矩阵的最大特征值 λmax=7.003 4，一致性指标 CI=(λ -n)/(n-1)=0.000 6，查表得与n=7对应的随机一致性指标RI=1.350，则一致性检验系数CR=CI/RI=0.000 4。CR≤0.1时，通过一致性检验，指标权重为有效。

表4 基础建设和园区规模的方案层指标数据表Tab.4 Index data of alternative layer in infrastructure and park size

2.2.3 B2的方案层指标权重。对于B2的方案层指标，问卷得到的相对重要性两两比较数据见表5。

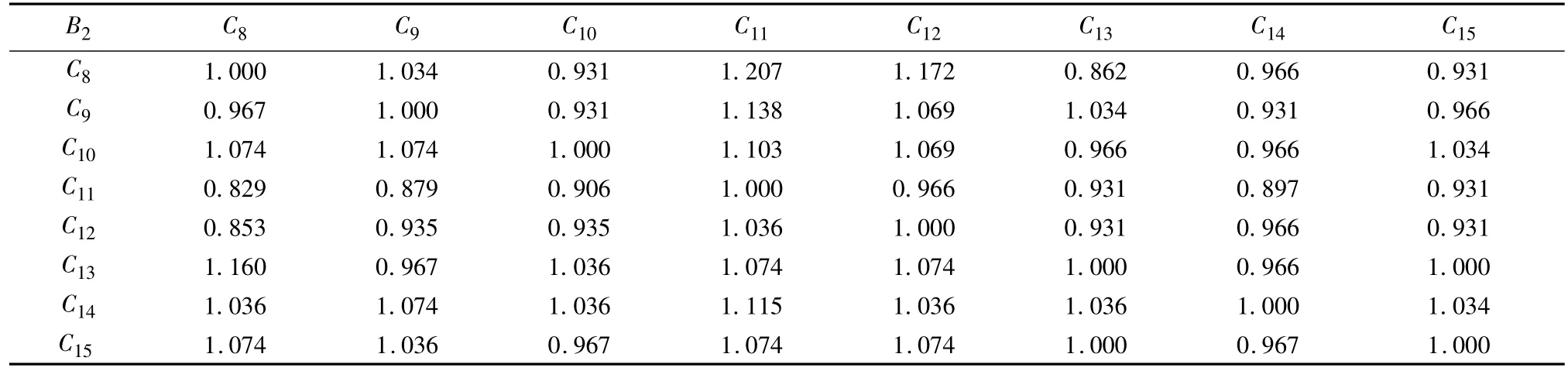
表5 区位优势和市场环境的方案层指标数据表Tab.5 Index data of alternative layer in location advantages and market environment

以表5的数据构成一个8×8的矩阵，用方根法进行归一化处理，得出B2的8个方案层指标权重分别为:0.125 7，0.125 2，0.129 2，0.114 4，0.118 3，0.129 0，0.130 5，0.127 7。同时，求得该矩阵的最大特征值 λmax=8.093 6，一致性指标 CI=(λ -n)/(n-1)=0.001 2，查表得与n=8对应的随机一致性指标RI=1.41，则一致性检验系数 CR=CI/RI=0.000 8。CR ≤0.1时，通过一致性检验，指标权重为有效。

2.2.4 B3的方案层指标权重。对于B3的方案层指标，问卷得到的相对重要性两两比较数据见表6。

以表6的数据构成一个7×7的矩阵，用方根法进行归一化处理，得出B3的7个方案层指标的权重分别为:0.147 0，0.144 9，0.145 7，0.136 9，0.138 0，0.152 3，0.135 2。同时，求得该矩阵的最大特征值 λmax=7.011 5，一致性指标 CI=(λ -n)/(n-1)=0.00 19，查表得与n=7对应的随机一致性指标RI=1.350，则一致性检验系数CR=CI/RI=0.001 4。CR≤0.1时，通过一致性检验，指标权重为有效。

表6 产业链条和企业发展的方案层指标数据表Tab.6 Index data of alternative layer in the industry chain and the development of the enterprises

2.2.5 B4的方案层指标权重。对于B4的方案层指标，问卷得到的相对重要性两两比较数据见表7。

以表7的数据构成一个8×8的矩阵，用方根法进行归一化处理，得出B4的8个方案层指标的权重分别为:0.135 0，0.118 4，0.126 5，0.120 8，0.126 5，0.123 5，0.121 0，0.128 3。同时，求得该矩阵的最 大特征值λmax=8.0075，一致性指标CI=(λ -n)/(n-1)=0.001 1，查表得与n=8对应的随机一致性指标RI=1.41，则一致性检验系数 CR=CI/RI=0.000 8。CR ≤0.1时，通过一致性检验，指标权重为有效。

表7 科技创新和人力资本的方案层指标数据表Tab.7 Index data of alternative layer in science and technology innovation and human capital

2.2.6 B5的方案层指标权重。对于B5的方案层指标，问卷得到的相对重要性两两比较数据见表8。

表8 园区管理和公共服务的方案层指标数据表Tab.8 Index data of alternative layer in park management and public service

以表8的数据构成一个9×9的矩阵，用方根法进行归一化处理，得出B5的9个方案层指标的权重分别为:0.108 8，0.111 4，0.112 7，0.109 0，0.117 7，0.115 4，0.107 1，0.108 6，0.109 4。同时，求得该矩阵的最大特征值 λmax=9.005 9，一致性指标CI=(λ -n)/(n-1)=0.000 7，查表得与n=9对应的随机一致性指标RI=1.46，则一致性检验系数 CR=CI/RI=0.000 5。CR ≤0.1时，通过一致性检验，指标权重为有效。

2.2.7 B6的方案层指标权重。对于B6的方案层指标，问卷得到的相对重要性两两比较数据见表9。

表9 政府扶持和政策优惠的方案层指标数据表Tab.9 Index data of alternative layer in government support and preferential policy

以表9的数据构成一个6×6的矩阵，用方根法进行归一化处理，得出B6的6个方案层指标的权重分别为:0.173 0，0.170 1，0.176 9，0.163 8，0.161 0，0.155 1。同时，求得该矩阵的最大特征值λmax=6.001，一致性指标 CI=(λ -n)/(n-1)=0.000 2，查表得与n=6对应的随机一致性指标RI=1.255，则一致性检验系数CR=CI/RI=0.000 2。CR≤0.1时，通过一致性检验，指标权重为有效。

3 竞争力指标体系的应用展望

3.1 指标体系的完善

确定了现代农业科技园区竞争力评价指标体系，以及指标体系中准则层和方案层指标的各自权重。可以发现，准则层各指标权重之和等于1，如果以百分制评价，则将6个准则层指标的权重乘以100即可。对于方案层指标权重的具体分值来说，还需要乘以其隶属的准则层权重来确定，例如，准则层“基础建设和园区规模”的指标权重为0.162 6，其下属的7个方案层指标权重分别为 0.147 8，0.146 1，0.136 6，0.135 0，0.141 2，0.137 3，0.155 9，则在整个指标体系中的权重分别为0.024 0，0.023 7，0.022 2，0.021 9，0.023 0，0.022 3，0.025 4，以百分计算，均为二点几分，其余方案层指标以此类推，评价者即可以据此对方案层各项指标打分评价。

现代农业科技园区竞争力评价是一项复杂的事情，指标体系也比较繁琐，有些方案层指标是标准量化的，例如人口数量，客观性强，不受主观影响，有些方案层指标则是非标准量化的，例如投资环境改善，可能不同的评价者打分略有差异。为了尽量避免评价者的主观性，需要对各个方案层指标的具体打分方法进行必要的说明，也可以认为是其中一些指标还可以细分。此外，还需要根据参与评价的现代农业科技园区对象，对于具体的打分取值等做出说明，使得评价标准和过程更加公允。例如，一个西部地区的县级园区，可能“辐射的消费人口总数”仅为几万人，而北京市的一个国家级园区，“辐射的消费人口总数”可能几百万甚至上千万，如果二者相比此项，北京园区打满分，是不是此项目下县级园区只是北京园区得分的百分之一呢?这样未免过于悬殊，可以在评价时加以限定，比如采用分档制，分为100万人、10万人、1万人，各档级的得分差距不宜太大。

可见，尽管构建了完整的现代农业科技园区竞争力评价指标体系，但是在具体应用中还需要灵活把握和进一步细化。

3.2 指标体系的应用分析

现代农业科技园区竞争力评价指标体系具有较多的用途，结合本次研究，其用途主要体现在以下方面。

一是进行科技园区认定。例如，2011年陕西省认定了一批省级的现代农业科技园区，认定过程中对申报的各个园区进行量化打分，分高者获得认定，其认定过程也部分采用了竞争力评价指标体系，和本指标体系有许多暗合之处。

二是企业投资决策的应用。企业进入到新的区域拓展，究竟到哪里落户，是一个值得认真考虑的问题，因为选址不当企业被迫搬迁的案例很多。企业选址显然会评价入驻园区的竞争力，此时，园区竞争力评价指标体系很有用场，当然，在评价过程中企业可以依据自己的需要增减部分指标。

三是进行园区之间的一般比较。即使是两个表面上不大相干的现代农业科技园区，也可以利用竞争力评价指标体系进行一般比较，找到各自的优点和缺点，帮助园区取长补短、相互促进，实现规范化、持续、快速地发展。例如，本研究下一步将对陕西杨凌农业高新技术产业示范区和北京昌平国家农业科技园区进行竞争力评价比较，以帮助两个园区相互借鉴，各自提升自己的发展潜力。

3.3 研究展望

本研究分析了现代农业科技园区竞争力要素，构建了一个完整的现代农业科技园区竞争力评价指标体系。但是，目前该指标体系的应用实践、反馈和改进还没有完成，需要下一步深入研究。同时，对于方案层指标在应用中应该注意的问题、可以进一步细分的地方、有必要作出某些限定的说明等也需要进一步讨论和探索。

总之，随着现代农业和产业园区的发展，现代农业科技园区竞争力评价指标体系具有较强的理论和实践价值，作者将不断深入地进行探究。

［1］蒋和平，辛岭.建设中国现代农业的思路与实践［M］.北京:中国农业出版社，2008:22-25.

［2］韩长赋.加快发展现代农业［J］.农业技术与装备，2011(2):4-5.

［3］张长海.现代农业科技园区创新发展模式探索研究［J］.广东农业科学，2012，39(11):224-226.

［4］董理.发展现代农业园区的经济政策研究——基于漯河市农业园区调查分析［J］.漯河职业技术学院学报，2012，11(4):100-102.

［5］周成，陈焕容，杜明辉.现代农业科技园区的配套与保障体系建设探索［J］.现代化农业，2012(5):49-50.

［6］雷广海，方斌，刘友兆.发展中的现代农业园区用地思路与对策探讨［J］.地域研究与开发，2008，27(1):94-97.

［7］田逢军.近年来我国观光农业研究综述［J］.地域研究与开发，2007，26(1):107-112.

［8］翟虎渠，曾希柏，沈贵银，等.现代农业科技园区评价指标体系研究［J］.农业现代化研究，2003，24(1):40-44.

［9］王欧，吴文良.中国农业科技园区评价指标体系研究［J］.农业技术经济，2003(4):25-28.

［10］钟甫宁，孙江明.农业科技示范园区评价指标体系的设立［J］.农业开发研究，2007，13(1):21-27.

［11］王宗军，蒋元涛.基于SWOT的智能型动态战略决策支持系统的分析和实现［J］.系统工程，2004，22(4):73-76.

［12］赵文，朱继涛.波特五力竞争模型及其拓展应用［J］.中国外资，2009(11):149.

［13］李天舒.“结构-行为-绩效”范式的理论演进与现实应用［J］.改革与战略，2008，24(7):109-111.

［14］Porter M E.The Competitive Advantage of Nations［M］.New York:The Free Press，1990.