“力的独立作用原理”处理曲线运动的优越性
陈晓斌 许忠艳
(辉南县第一中学 吉林 通化 135100)
“力的独立作用原理”虽然没有作为教学内容在教材中出现,但在解题时,我们有时却在不自觉的运用.理解好这一原理,不但可以使学生在遇到复杂问题时,能找到巧妙简捷的处理方法,更能加深对力和运动关系、做功与能量转化关系的理解,提高学生的物理思维能力.
本文试从 “运动和力”的关系、“做功与能量转化”的关系,这两个角度来阐释力的独立作用原理处理复杂曲线运动中的优越性.
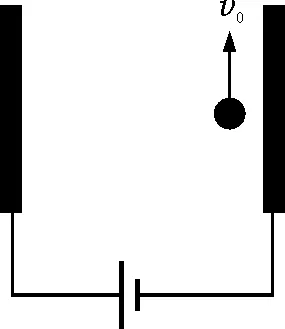
图1
【例1】一个带负电的小球,质量为M,电荷量为Q.在一个如图1所示的平行板电容器的右侧板边被竖直上抛,最后落在电容器左侧板边同一高度处.若电容器极板是竖直放置,两板间距离为d,板间电压为U,求电荷能达到的最大高度及抛出时的初速度.
解析:根据力的独立作用原理,小球受到两个力的作用:重力使它在竖直方向做竖直上抛运动,水平向左的电场力使之在水平方向向左做匀加速直线运动,二者互不影响.二个方向唯一有联系的量就是时间相等!
在水平方向,由牛顿第二定律和运动学公式,可得
在竖直方向,由竖直上抛运动的对称性可知,上升到最高点与返回到同一高处的时间相等,都等于水平方向运动时间的一半.电荷达到的最大高度和抛出时的初速度分别为
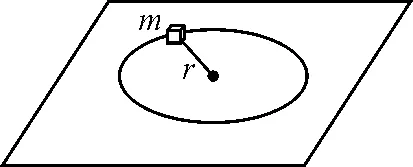
图2
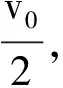
B.绳拉力的大小随物体转过的角度均匀减小
C.如果初速度v0较小,绳的拉力可能为零
解析:在高中阶段求解时间用到的运动学公式的成立条件都是匀变速直线运动,此题却是变速曲线运动!但如果运用力的独立作用原理,可知做变速曲线运动的小方块在水平面内的受力有两个:一个是沿切向的滑动摩擦力,使小方块做匀减速曲线运动;另一个是沿径向的拉力,做圆周运动的向心力,因与运动方向垂直,故不改变运动的快慢,即与运动时间无关.因此可将匀减速曲线运动“化曲为直”,运用匀变速直线运动的公式来求解,只是把“位移”换成“弧长” .
运动一周的时间
选项A正确;
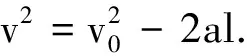
选项B正确,选项C错误;
在切向,摩擦力做功,由动能定理得
【例3】一带电粒子以速度v0沿竖直方向垂直进入匀强电场E中,如图3所示.经过一段时间后,其速度变为水平方向,大小仍为v0.则有
A.电场力与重力大小相等
B.粒子运动的水平位移大小等于竖直位移大小
C.电场力所做的功一定等于重力所做的负功
D.电势能的减小一定等于重力势能的增大
HIV感染儿童应尽早开始HAART,如果没有及时HAART,艾滋病相关病死率在出生后第1年达到20%~30%,第2年可以超过50%。
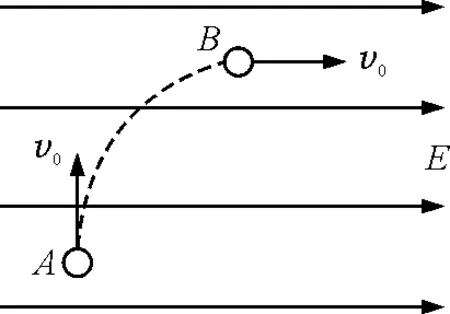
图3
解析:粒子从A到B,“速度变为水平方向”,说明竖直方向速度由v0减小到零,由此可以判定粒子一定受到竖直向下的重力.在解答时如果处理不当,答案不容易选全.
选取水平沿E为坐标轴x的正方向,坚直向下为y轴的正方向.
由力的独立作用原理可知,粒子x方向在电场力的作用下做匀加速直线运动,y方向在重力的作用下竖直上抛运动,两个力的作用彼此独立,互不影响,解答起来简洁明了.
在相同的时间内两个方向的速度的改变量的大小均相等, 故ax=g,F=G,所以选项A正确;
两个方向的力各自做功,由动能定理得,Fx-Gh=0,得x=h, 选项B和选项C正确;
水平电场力做正功,电势能减少,竖直方向重力做负功, 重力势能增加;选项D正确.
【例4】在场强为B的水平匀强磁场中,一质量为m,带正电q的小球在O点静止释放,小球的运动曲线如图4所示.已知此曲线在最低点的曲率半径为该点到x轴距离的2倍,重力加速度为g.求:
(1)小球运动到任意位置P(x,y)的速率v.
(2)小球在运动过程中第一次下降的最大距离ym.
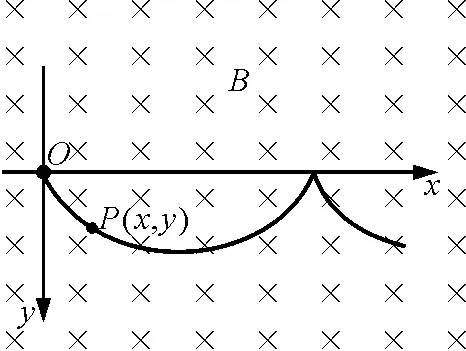
图4
解析:带电粒子的运动属于复杂的曲线运动,分析可知在第(1)、(2)问受到受到二个力,第(3)问受到三个力的作用,运用力的独立作用原理对小球做两方面的分析.
(1)从做功的角度来分析:重力、电场力、洛伦兹力对小球的作用互不影响,重力、电场力做功特点是与路径无关,而洛伦兹力始终不做功.
(2)从运动和力的角度来分析:开始在重力(后来是电场力与重力的合力)作用下使小球向下(后向上)做加速运动,并被洛伦兹力改变其方向,当速度方向变为水平时,做功最多、速度最大;之后向上(后向下)弯曲而做减速运动,直到速度减为零,再重复刚才的运动,如图4(后如图5)所示.
题中的三个问题中所求的量都与过程无关.因此可以不考虑物体运动的具体性质,用动能定理处理更简洁明快.
(1)洛伦兹力不做功,只有重力做功,由动能定理得
(1)

(2)
(2)设在最大距离ym处的速率为vm,根据圆周运动有
(3)
(4)
由式(3)、(4)与R=2ym,得
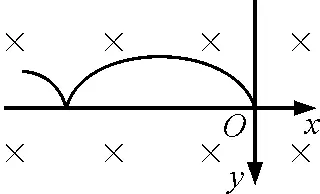
图5
(3)小球运动如图5所示.
由动能定理
(5)
由圆周运动
(6)
由式(5)、(6)及R=2|ym|,解得
可见,力的独立作用原理不仅体现在利用运动的合成与分解时,采用 “化曲为直”的方式来处理抛体运动(如平抛运动、类平抛运动等),还体现在“功与能量转化”中总功的计算上,在处理曲线问题时具有一定的优越性,充分认识力的独立作用原理,可深化对“运动合成与分解”的理解,更加灵活自主地运用动能定理、机械能守恒定律,使复杂问题简单化,提高分析、解决复杂问题的能力,提高学生的物理思维水平.
参考文献
1 梁敬纯,等.运动的独立性与力的独立作用原理(一).物理通报,1998(8):7~9
2 周誉蔼,等.运动的独立性与力的独立作用原理(二).物理通报,1998(9):8~10

