基于突变理论的工业园区环境承载力动态评价方法

徐琳瑜,康 鹏,刘仁志 (北京师范大学环境学院,环境模拟与污染控制国家重点联合实验室,北京 100875)

工业园区是集社会经济发展、资源环境消耗、人口于一体的面积较小的区域,在有限的面积内使经济得到快速稳定的发展,其资源环境必定承受一定的发展压力,探讨其经济社会发展是否在资源环境的可承受范围内具有一定的实际意义[1-2].工业园区可持续发展的本质是资源环境系统的持续承载,因此可持续发展必须建立在生态系统完整、资源持续供给和环境长期有容纳量的基础上[3-4].

目前环境承载力一般涉及到城市、流域等,相关的环境承载力定义比较成熟.区域环境承载力是指在一定的区域范围内,在维持区域环境质量不发生质改变的条件下,区域环境系统所能承受人类各种社会经济活动的能力[5-6].对环境承载力的研究不仅关注量约束,并且考虑到质的影响,同时将社会经济要素纳入承载体系中.迄今为止文献研究中较少有将环境承载力应用于工业园区发展规划的实例[7-8].

环境承载力分析是区域环境问题研究的核心内容[9-11].目前运用到工业园区环境承载力评价方法较少,主要涉及到指标体系评价方法以及机理分析方法如层次分析法、多目标规划方法[12].有些学者基于工业园区承载力的概念建立分级指标体系结合层次分析法应用到工业园区范畴[13-14].上述评价方法与模型在一定程度上开拓了工业园区环境承载力评价方法.由于园区系统的复杂性和模糊性,在其环境承载力的理论体系、评价指标及定量评价方法仍需进一步研究.依据上述分析,本文将工业园区环境承载力定义为:一定时期内,在保证园区可利用资源环境容量的合理利用、生态环境结构稳定和功能正常前提下,园区复合系统能够承受社会经济压力的能力.

珠海富山工业园是珠海市四大工业园区之一,用地规模为151.59km2,规划目标是形成电子信息、机械制造的优势产业集群,初步建成以船舶工程、车辆制造等为核心的临港产业集群以及以新能源、新技术、新材料为主的先进制造业集群,生态环境安全格局基本形成,循环经济体系逐步完善,生态环境良性循环.由于园区发展表现出非线性、非连续等特征,而针对工业园区发展环境承载力评价较难体现这种非连续、阶跃式的数理特征,尤其是考虑承载力系统潜在突变特性的研究还鲜见报道.因此本文将突变理论运用到富山工业园区环境承载力的发展趋势研究,旨在解决工业园区环境承载力评价技术难点.构建突级变数法评价模型分析环境承载力的演变规律,通过相关情景分析方法,对其规划不同情境下环境承载力变化趋势进行评价分析.

2 工业园区环境承载力动态评价模型

突变理论的主要特点如下:1)突变理论可依据内部状态变量和外部控制参量来描述自身系统行为,以及环境承载力指标体系,这里自然环境承载可理解为内部状态变量,而外部控制参量可认为是人为环境承载力;2)可通过归一化方法把突变系统内诸控制变量的不同质态统一为同一质态,能够对不同时期下系统开展动态评价,特别针对工业园区规划发展中环境承载力动态变化趋势,该方法能够综合考虑规划发展工业园区影响不同的因素,对不同时期下环境承载力状态进行客观评价.因此,突级变数法适用于工业园区环境承载力动态评价.

2.1 环境承载力动态评价理论

20世纪80年代,法国科学家托姆提出了结构稳定性和形态形成学,明确地阐明突变理论.所谓突变理论是指在系统演化过程中,某些变量的连续逐渐变化最终导致系统状态的突然变化,即从一种稳定的状态跃到另外一种稳定的状态,提供了一种研究不连续性、质变突然产生和跃迁的普遍适应的方法[15].

表1 常见突变模型分歧方程Table 1 Common difference equations of mutation model

突变级数法的理论基础是突变理论,主要利用动态系统的拓扑理论构造数学模型,从描述、预测自然现象与社会活动中事物连续性中断的质变过程.势函数通过状态变量和外部控制参量来描述系统行为“突变理论”,将状态曲面的奇点集映射到控制空间,得到状态变量在控制空间的轨迹(分叉集),处于分叉集中的控制变量值会使势函数发生突变,即从一种质态跳跃到另一种质态[16].突变理论的突变级数法一般将评价多目标进行多层次分主次的矛盾分解排列,逐渐分解到下一层子指标,从而构建出树状目标层次结构.因此突变系统里某状态变量的控制变量一般不会超过4个,相对应的各层指标数通常也不超过4个.在表1中,x为突变系统中的一个状态变量;V(x)为状态变量x的势函数.在突变系统中,系统势函数的状态变量和控制变量是相互矛盾的两个方面.主要控制变量一般排在前,而次要控制变量排在后.如果一个指标可以分解为2个子指标,可视为尖点突变系统,依此类推,可以根据分解的指标数来确定突变模型.

2.2 评价指标体系

考虑到区域社会经济与环境系统的复杂性和多样性,衡量环境承载力的指标体系难以涵盖区域所有活动,也不可能统一规定所有的指标,因此要从各子系统中选择有代表性、易量化的指标做定性与定量相结合的分析[17].同时,对于工业园区这类不完全的人工生态系统,其自然资源的供给很大程度上依赖于腹地的支持,因此其所处的区域资源供给水平决定着其自然承载力.针对富山工业园区资源和环境态势,根据园区现有经济、技术开发条件下园区规划发展对自然生态环境和生活质量可能产生的影响,建立环境承载力指标体系(ECCI),包括自然环境承载力(NECC)和人为环境承载力共同组成的环境承载力(HECC).

表2所示指标体系中,各类污染物环境容量剩余承载率等于该污染物环境容量减去污染物排放量与其环境容量的比值,水资源供需比等于园区各类活动的需水量(人口、工业活动、道路、人均绿地)与水资源供给和需求的比值,能源供需比类似.

2.3 基于熵权的突变模型构建

利用归一化公式进行综合评价,状态变量所对应的各个控制变量计算出的值可以按照互补准则进行计算获取.若系统各控制变量之间可互相弥补其不足时,按其均值取用.

表2 工业园区综合环境承载力指标体系(ECCI)Table 2 Index system of environmental carrying capacity of an industrial park

每一层次中的各个指标按其相对重要性进行排序,利用熵权法对各级指标按照重要程度排序,建立递级突变模型.在信息论中,熵值反映了信息无序化程度,其值越小,系统无序度越小,故可用信息熵评价所获系统信息的有序度及其效用,即通过指标值构成的判断矩阵来确定指标权重.通过权重大小判断各指标的重要性,消除人为排序所存在的误差,使评价结果更符合实际.

为解决模型参数量纲统一的问题,同时使原始数据在消除量纲后的取值限制在0～1之间,需要对原始数据进行预处理.对数值越大越好的正向指标根据式 (1)、对数值越小越好的负向指标根据式(2)进行处理.

熵值反映了信息无序化程度,其值越小,系统无序度越小,故可用信息熵评价所获系统信息的有序度及其效用.由评价指标值构成的判断矩阵来确定指标权重,它能尽量消除各指标权重计算的人为干扰,使评价结果更符合实际,其计算步骤如下:

1)根据熵理论,定义m个评价事物n个评价指标的熵值,其中m为规划年限,m值为2007～2030年,m为24,n为环境承载力评价指标个数,n为13.可以确定评价指标的熵为

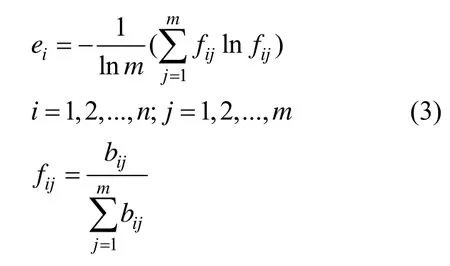
式中:ei为第i项指标的信息熵值;fij为标准化值;bij为运用上式(1)或式(2)指标无量纲化值.

利用熵值法估算各指标的权重,其本质是利用该指标信息的价值系数来计算,其价值系数越高,对评价的重要性就越大.最后可以得到第i项指标的权重:

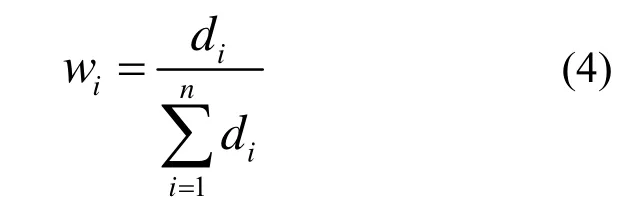
运用式(1)～式(4)依据上述方法依次求出各指标值的权重大小,见表3.

表3 环境承载力指标值权重确定Table 3 Index weighting factors of environmental carrying capacity

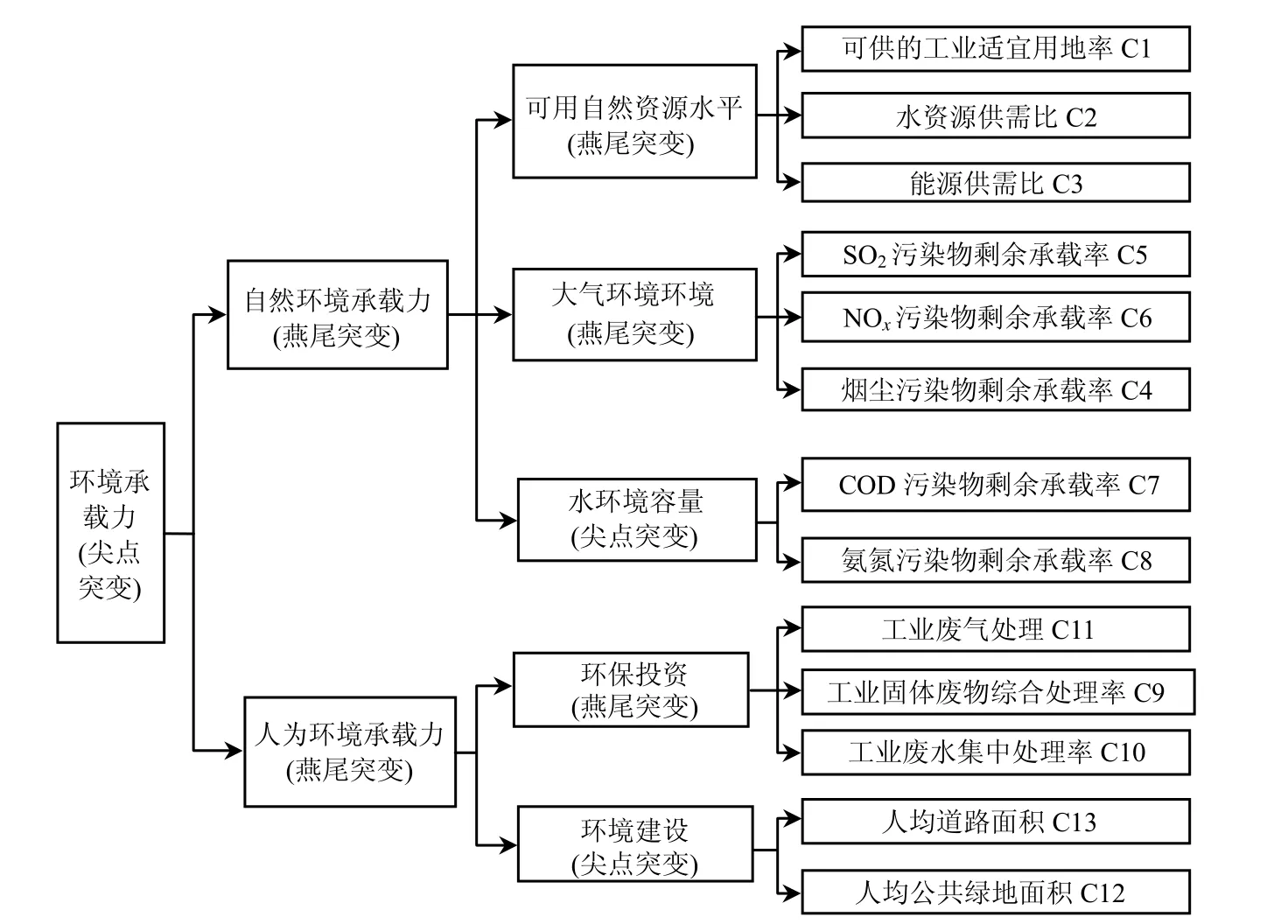
图1 园区环境承载力突变级数法评价结构Fig.1 Catastrophe progression of evaluating model on environmental carrying capacity of an industrial park

依据上述权重计算方法,在模型的构建过程中,将评价总指标进行多层次矛盾分解,构成树状目标层次结构,从评价总指标到下层指标再到下层子指标,原始数据只需要知道最下层指标的数据即可,而同一指标的下一级指标通过相互间重要程度进行对比排序,即重要指标排在前、次要指标排在后.

根据上述权重结果及控制变量维数,构建富山工业园区环境承载力突变评价结构如图1所示.

2.4 评价的分级标准

由于归一公式的特点,突变级数法计算得出的评价值一般较高,很难从常规上对其“优”、“劣”做出直观判断.因此,根据研究区域特点,在常规的等级标准基础上,制定出适应自身特点的等级标准,这是本研究具有实用价值的关键.常规等级标准将安全度由低到高依次划分为5个评价等级,将区域环境承载力评价标准分类为弱承载力、较弱承载力、适中承载力、较高承载力,高承载力最终结果见表4.以上设定的环境承载力综合指数分别为0.2、0.4、0.6、0.8、1.0,需将绝对意义下各级承载指数转换为突变级数法下的各级综合评价值,进而制定出突变级数法下的各级分级标准.

研究中评价标准转换思路为:在指标体系给定的前提下,设指标层各指标相对隶属度均为x,从理论意义上讲,此时评价指标体系的准则层、目标层各指标隶属度也均应为x,然后根据图1中相应的突变模型可计算出该等级下准则层和目标层的综合评价值(表4).

表4 环境承载力评价等级标准Table 4 Evaluation standards of environmental carrying capacity

3 富山工业园区环境承载力动态评价

3.1 环境承载力指标值的动态预测

建立工业园区环境承载力指标系统动力学关系,用以预测各指标在不同年份的数值.

根据工业园区各产业主要资源消耗,针对水、大气、固废等生态环境要素,考虑各类污染物处理率和处理量,通过现有园区的污染物处理设施规模及水平来预测模拟园区最终污染物的排放量,同时兼顾园区主要污染物的环境容量,计算得出各环境要素中承载剩余的状态.

环境子系统由大量复杂的参数和关系式构成,以水环境污染物产生以及处理为例,园区水资源供需和工业活动对水环境影响主要通过不同工业行业的万元需水量以、废水产生率和废水中产生COD、氨氮来表征,环境保护效果由废水处理率和废水中污染物总量下降率来表现,其数量关系式如式(5)～式(8)所示.系统模拟如图2所示.

依此方法,同时构建大气环境和固废STELLA模拟关系.此外,在资源供需部分考虑园区水体供需能力,能源供需方面的模拟、固体废物处理设施建设以及相关基础设施的建设,主要参考珠海市相关的基础设施建设规划及其园区发展建设规划.

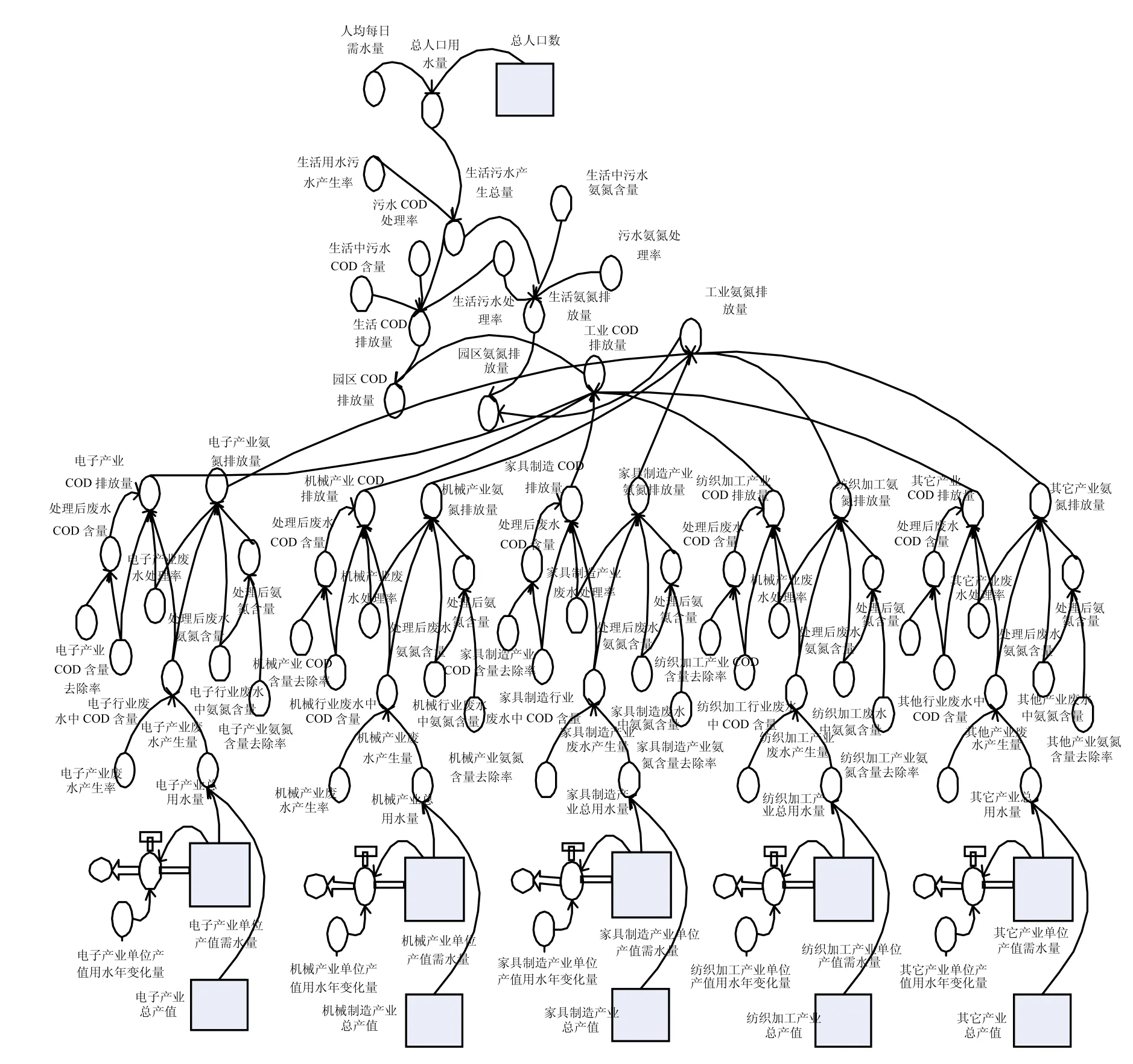
图2 富山工业园区环境子系统中水环境部分STELLA模拟示意Fig.2 Water environment system model in Fushan industrial park of the dynamic system simulation

依据富山工业园区工业行业的特点,将其工业行业类型分为电子信息产业、机械制造产业、建材家居产业、纺织加工产业和其他产业.经济子系统中参数包括起始年的各类行业的工业产值,各类行业的发展增长速率,以及水资源和能源需求.该子系统用园区工业总产值作为状态变量,各类工业园区不同行业发展的增长速率主要参考园区工业行业规划发展.园区人口子系统,以区域人口作为状态变量;园区年出生人口、园区年死亡人口、园区年净迁人人口作为速率变量,其环境属性主要通过人均用水量,生活污水产生系数、生活污水中COD和氨氮含量,通过连接生活污水处理达标率,处理过程中污染物的降低量.其参数关系式如式(9)～式(12)所示,园区发展模型构建如图3所示.

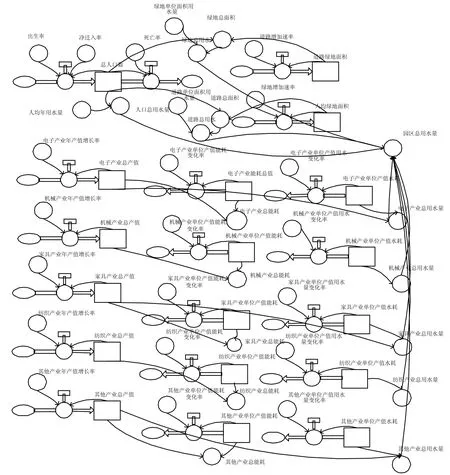
图3 富山工业园区人口经济发展STELLA模拟示意Fig.3 Population and ecomonic development model based on the dynamic system simulation in Fushan industrial park

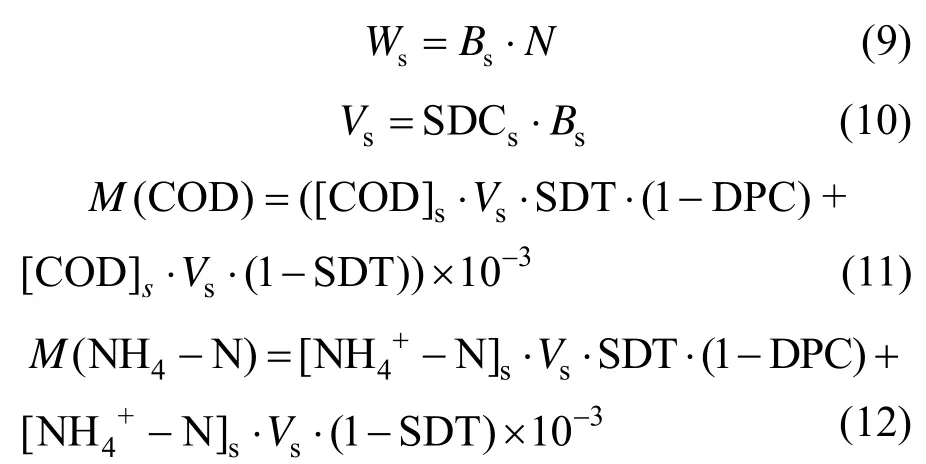
式中:Ws为园区人口总需水量,t;Bs为人均生活用水量,t/人;N为园区总人口数;Vs为生活污水产生量,t;SDCs为生活用水污水产生率;M(COD)为人口COD总排放量,t;[COD]s为生活污水中COD的浓度,kg/m3;M(NH4+-N)为人口氨氮总排放量,t;[NH4+-N]s为生活污水氨氮的浓度,kg/m3;SDT为污水处理率;DPC为处理过程中污染物下降比例.

对系统动力学模型检验目的是验证所建立的模型是否较好地反映系统的本质特征和主要的环节.选取园区总人口、工业总产值、总用水量和水体、大气污染物排放总量和固体废物排放量等主要指标为代表,另外一些主要规划预期值也作为模型检验的重要依据.结合两者的数据,以2007年为起始,输出预测2010年的模拟结果,与历史数据比较误差＜2%的概率为52.6%,误差＜5%的概率为87.5%,误差＜10%的概率为95.7%,说明模型有足够的有效性.

3.2 环境承载力动态评价结果

收集富山工业园现状数据,并根据所建立系统动力学关系模型预测各指标在2007～2030年数值,利用所构建的评价模型开展工业园区环境承载力评价,结果见表5.

表5 富山工业园区环境承载力评价结果Table 5 Results of environmental carrying capacity assessment in Fushan industrial park

从自然环境承载力评价来看,由于园区大规模产业规模和人口规模迁入,不断增加的工业生产生活活动消耗大量的资源环境的容量,由最初的第二等级下降到规划末期的第四等级,环境承载力下降的幅度不大,其下降速率随规划发展越来越快.从人为环境承载力来看,其评价值由最初的第三等级上升到规划末期的第二等级,从上述的趋势来看,规划初期上升的速度太快,主要得益于园区基础设施建设所取得的效益,但到了园区规划的末期,园区上升的趋势不如规划初期那么明显.

通过对工业园区规划建设中环境承载力分析得出:工业园区环境承载力评价主要由自然环境承载力和人为环境承载力构成的燕尾突变.结合表4和表5对比分析可以看出,由规划基准年处于第二等级,初期的园区建设对其环境承载力影响不大,到规划初期末2015年,环境承载力呈现出一定上升的趋势,上升幅度不大,伴随着一定的波动.随着园区的社会经济活动进一步建设,由于工业园区规划建设的发展,资源环境的消耗,到了规划后期环境承载力出现了一定下降的趋势,但园区环境承载力下降趋势不大,仍处于同一等级.

3.3 规划情景分析

由于富山工业园区处于规划建设初期,园区建设还存在较大的不确定性和随机性,在前面研究的基础上,进一步提出相应的环境保护措施.在上述基础上建立好园区动态预测模型基础上,设定不同情景发展的趋势,其各种情景构建如下:

情景1,保持富山工业园区现有发展趋势下,参考广东省有关污染物处理设施投资情况,设定各种污染物产生系数随科学技术水平提高而下降的情景见表6:

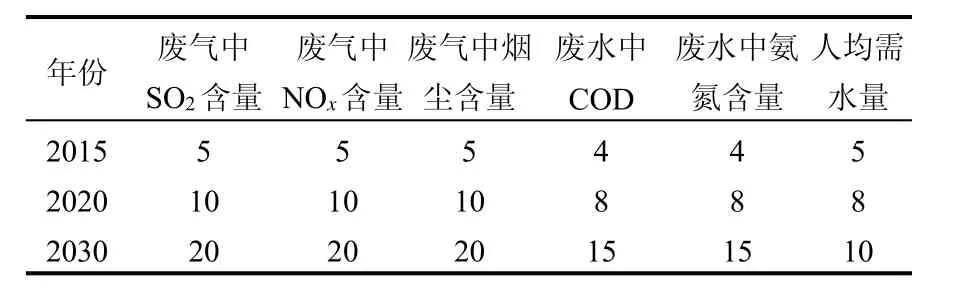
表6 情景1中不同规划年污染物含量(%)Table 6 Content of the pollutant in environment of different planning year under scenario 1(%)

情景2,参考国内先进工业园区发展的趋势,主要参考其工业单位产值能耗和污染物排放水平,具体排放趋势见表7:

表7 国内先进工业园区万元产值污染物排放和能耗水平Table 7 Pollutant emission and energy consumption per 1,0000 Yuan RMB in advanced industrial park

情景3,参考国内工业园区的发展趋势,通过已经建立好的系统动力学模型进行模拟,结合情景一下各环境介质中污染物下降水平及大小,设计降低有关污染物参数来模拟发展变化趋势.

运用突变级数法对3种情景下其环境承载力进行评价.评价结果如表8所示.

利用突变级数法对工业园区规划建设中环境承载力进行评价的结论如下:工业园区环境承载力主要是自然环境承载力和人为环境承载力构成的燕尾突变.3种情景下的环境承载力变化趋势基本一致,都是规划中前期上升,中期出现一定波动,中后期出现一定程度的下降.情景2评价值在规划中后期之前都大于情景1,到了规划中后期,情景2评价值略低于情景1评价值.而情景3的数值都高于情景1和情景2的数值,而注意到到规划末期,末期下降趋势明显比前两者低.

通过上述情景分析得出,伴随着园区发展,各种污水、废气的排放量也相应增加,虽然园区现有生态环境保护基础设施建设会在一定程度上缓解园区发展对生态环境的影响,但仍具有提高环境承载力的潜力.因此提倡通过发展循环经济,进一步加强完善生态环境保护基础设施建设,加大节能、降耗与消减污染物的力度;从工业生活的节水与工业废水重复利用的角度,提高水资源的利用效率,减少工业园经济社会活动对其生态环境的影响,协调富山工业园社会经济与生态环境保护的关系,工业园在规划建设期间,合理有效地利用前期所余留的环境承载力.

表8 不同发展情景下的环境承载力评价值Table 8 Results of environmental carrying capacity assessment under different scenarios

4 结论

4.1 本文利用系统动力学构建的递级突变模型可从内外两种作用角度动态评估环境承载力和压力的变化趋势.

4.2 研究表明园区自然环境承载力于规划中后期处于下降的趋势,下降的趋势伴随着园区规划发展速率越快;而人为环境承载力伴随着园区规划建设处于上升趋势,规划建设初期的上升趋势最为迅速.

4.3 研究所构建评价模型科学合理,可用于工业园区规划发展中环境承载力评价,也可对工业园区规划发展提供合理科学的建议.

[1] 毛小苓,赵智杰,张 辉,等.经济开放地区工业园项目环境影响评价的特点 [J].应用基础与工程科学学报,2002,10(1):18-24.

[2]Geng Y,Cote R.Environmental management system at the industrialpark level[J].EnvironmentalManagement,2003,31(6):784-794.

[3]Park H S,Rene R E,Choi S M,et al.Strategies for sustainable development of industrial park in Ulsan,South Korea—from spontaneous evolution to systematic expansion of industrial symbiosis [J]. Environmental Management,2008,87:1-13.

[4]常春芝.环境承载力分析在规划环境影响评价中的应用[J].气象与环境学报,2007,23:39-41.

[5] 王 俭,孙铁珩,李培军,等.环境承载力研究进展 [J].应用生态学报,2005,16(4):768-772.

[6] 徐琳瑜,杨志峰,李 巍.城市生态系统承载力研究进展[J].城市环境与城市生态,2003,16(6):60-62.

[7]韦 静,曾维华.生态承载力约束下的区域可持续发展的动态模拟——以博鳌特别规划区为例 [J].中国环境科学,2009,29(3):330-336.

[8] 赵一平,朱庆华,耿 勇,等.基于生态承载力的工业园区可持续发展评价浅析 [J].科学学研究,2004,22:56-60.

[9] 毛汉英,余丹林.区域承载力定量研究方法探讨 [J].地球科学进展,2001,16(4):549-555.

[10]黄常锋,何伦志.相对资源承载力模型改进及其应用 [J].中国环境科学,2012,32(2):366-372.

[11]Kyushik O,Yeunwoo J,Lee D K,et al.Determining development density using the urban carrying capacity assessment system[J].Landscape and Urban Planning,2005,73:52-59.

[12]曾维华,杨月梅.环境承载力不确定性多目标优化模型及其应用——以北京市通州区区域战略环境影响评价为例[J].中国环境科学,2008,28(5):667-672.

[13]赵一平,朱庆华.工业园区生态系统承载力评价方法研究[J].工业技术经济,2007,26(1):42-45.

[14]朱宇兵.广西北部湾经济区环境承载力预警系统研究[J].东南亚纵横,2009,7:59-62.

[15]凌复华.突变理论及其应用 [M]．上海:上海交通大学出版社,1987.

[16]陈云峰,孙殿义,陆根法．突变级数法在生态适宜性评价中的应用——以镇江新区为例 [J].生态学报,2006,26(8):2587-2593.

[17]Berck P,Levy A,Chowdhury K.An analysis of the world's environment and population dynamics with varying carrying capacity,concernsand skepticism [J].Ecological Economics,2012,73(0):103-112.

致谢：论文英文摘要及英文图表标题由尹心安博士帮忙修改语言.