射流总压和角度对气动喉道控制喷管的影响①
王如根,郭飞飞,吴培根,罗 凯
(空军工程大学航空航天工程学院,西安 710038)
0 引言
固体火箭发动机推力控制包括推力矢量控制和推力大小控制。固定几何结构气动矢量喷管,通过气流射流来实现推力矢量控制和喉道控制(通过喉道控制进行推力大小控制),无需传统的控制机构,能实质上减少喷管重量、降低成本与特征信号、提高可靠性[1],不仅可应用于火箭发动机,而且可应用于航空发动机,在国内外得到了迅速发展[2-8]。不论气动矢量控制还是气动喉道控制,目前各国都在寻找提高射流效率的方法,力求以最少的射流流量达到最好的控制效果。
本文采用基于雷诺平均的二维Navier-Stokes方程和RNGκ-ε湍流模型,对在喷管喉道附近注入不同压力、不同角度对称射流的固定几何结构二元收敛-扩张矢量喷管全流场进行了数值仿真,分析了射流压力和角度对喉道控制的作用,以及对喷管性能的影响。
1 物理模型和计算方法
喷管模型参考了NASA Langley研究中心的二元喷管型面设计[1],收敛段、喉道处采用圆弧连接,各几何参数如图1所示(单位:mm)。喷管出口面积与喉道面积之比为1.35,对应的喷管设计落压比5.034(如图1所示,图中还示出了射流角度α的规定,即射流方向与主流流动方向的夹角)。
计算域从喷管出口截面向上游、向下游和两侧分别延伸了6倍、10倍、6倍喷管长度。计算域被划分为13个子区域,分别生成网格后进行对接,对射流缝、壁面、喷管出口处网格进行等比加密。由于射流与主流的相互作用,流动情况较复杂,在计算过程中,还采用了网格自适应调整技术,保证调整后离壁面最近的网格单元y+在30~60之间,且相邻网格面积比小于10,所有网格单元都为四边形结构网格,网格总数52万多。图2为喷管及射流缝附近网格的局部放大图。
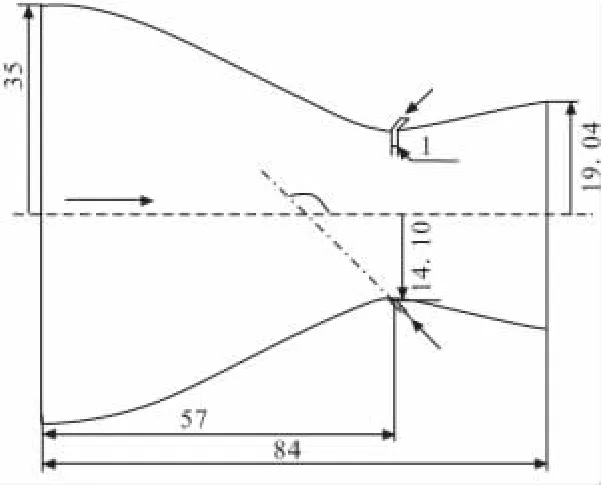
图1 喷管模型Fig.1 Model of nozzle

图2 喷管附近计算网格Fig.2 Grid near the nozzle
边界条件按下面方式给定:喷管进口和射流入口均为压力入口,给定总压、总温;出口为压力出口,给定静压;喷管外流入口给定黎曼边界条件;壁面采用绝热、无滑移物面条件。
喷管内外流场由连续方程、二维雷诺平均Navier-Stokes方程、能量方程、气体状态方程和Sutherland公式描述。方程的封闭采用RNG κ-ε湍流模型,并在壁面处结合标准壁面函数进行求解,文献[9]对3种湍流模型的计算结果进行了对比,表明RNG κ-ε湍流模型更适用于喷管射流流场的计算,文献[10]对本文所采用的数值计算方法进行了验证,详见文献内容。方程的求解采用时间推进的有限体积法,考虑到本文所研究的喷管内流动较复杂,选择具有高间断分辨率、高粘性分辨率和标量正值保持性的AUSM格式对方程进行空间离散[11]。
2 计算结果分析
本文保持喷管落压比不变(NPR=5.8,喷管处于轻度不完全膨胀状态),计算了4种射流与主流总压比(SPR=1.0、1.07、1.1、1.15)、5 种角度(α =60°、90°、120°、135°、150°),共20(4 ×5)种工况下的喷管流场。在此基础上,对计算结果进行整理,得到了喉部面积控制范围RTAC、喉部射流相对流量W·jet、喉道面积控制效率KTAC、总压恢复系数σ随射流角度α和射流与主流总压比SPR的变化关系。
其中,喉道面积控制范围(RTAC)用来评估射流对喷管有效喉道面积的影响;喉道面积控制效率(KTAC)用来比较射流控制效果的优劣,该值越大,说明控制同样的喉道面积变化范围需要的射流流量越小;总压恢复系数σ用来衡量射流对喷管性能的影响。
喉道面积控制范围(RTAC)的定义参考了文献[2],定义为无射流时的有效喉道面积减去有射流时的有效喉道面积所得的差,再除以无射流时的有效喉道面积所得的比值。

喉道面积控制效率(KTAC)定义为每百分之一的射流相对流量所能实现的喉道面积控制范围。

总压恢复系数σ定义为喷管出口总压除以喷管进口与射流进口总压的质量加权平均,即

2.1 射流角度和总压对喉道面积控制范围的影响
图3是喉道面积控制范围(RTAC)随SPR和α的变化情况。由图3可看出,在α不变的情况下,随SPR的增加,RTAC均逐渐增大,说明射流总压对气动喉道面积控制有明显作用;在SPR保持不变的情况下,随射流角度增加,相对喉道面积比先增大后减小,120°时有一极大值。说明射流角度对气动喉道面积控制有明显作用。在本文计算的20种工况下,RTAC最大值出现在 α =120°、SPR=1.15 时,其值为24.53%。
图4给出了不同射流角度下喷管出口速度分布。从图4可看出,α=120°时的气流出口马赫数要大于α=60°和α=1150°时的出口马赫数。结合图3可知,这是喷管有效喉道面积不同进而使得气流膨胀程度不同导致的。α=120°时的RTAC最大,有效喉道面积最小,气流膨胀程度最大,所以气流出口马赫数也大。α=60°和150°(SPR=1)时的RTAC值近似相等,两者的有效喉道面积相当,气流膨胀程度也就相当,因而两者的出口马赫数相当,只是马赫数分布略有不同。

图3 RTAC随SPR和α的变化Fig.3 RTAC vs SPR and α

图4 喷管出口马赫数(SPR=1)Fig.4 Mach number distribution along nozzle exit
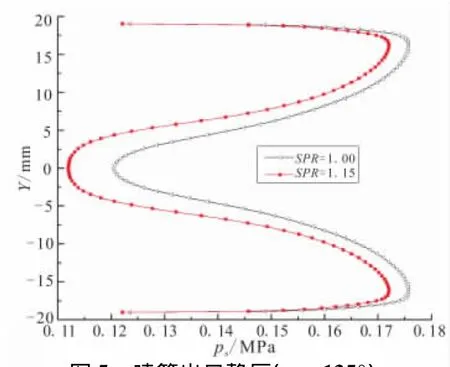
图5 喷管出口静压(α=135°)Fig.5 Static pressure distribution along nozzle exit
图5给出了不同SPR下喷管出口静压分布。结合图3可分析,SPR增大,RTAC增大,有效喉道面积减小,喷管膨胀比大,气流膨胀程度增大,出口马赫数增大,静压减小。程度,本文使用数理统计中有关二元方差分析的方法[12],作了对射流角度、射流总压对喉道面积控制范围的显著性检验(表1)。表1中,因素A代表射流角度α,因素B代表射流与主流总压比SPR,F表示符合F(n1,n2)分布的随机变量值。查F分布上侧分位数表可知,F0.005(4,12)=6.52,F0.005(3,12)=7.23,比较可得 FA>6.52,FB>7.23。所以,射流总压和射流角度对喉道面积控制范围都有显著影响,且射流角度的影响要大于射流总压的影响。

表1 二元方差分析结果Table 1 Analysis result of binary variance
2.2 射流角度和总压对射流相对流量的影响
表2给出了射流相对流量 W·jet随SPR和α的变化。从表2可知,随SPR的增加,W·jet总是增加的。这是因为NPR=5.8时,喷管处于不完全膨胀工作状态,根据流量公式(4),其流量与有效喉道面积及入口总压成正比,随SPR的增大,喷管有效喉道面积减小,主流流量减小,但对射流来说,当SPR增加时,射流总压增大,其流量总是增加的。所以,随SPR的增加,W·jet总是增加的。

从射流角度这一因素来看,射流相对流量在α=90°时普遍高于其他角度,这与文献[6]的结论是一致的。随着射流角度的增大,喷管有效喉道面积减小,主流流量是一直减小的,但变化程度较小;但射流流量则不同,当α从60°增加到90°时,射流有效流通面积增大(式(5),射流角度变化时,射流缝出口宽度保持不变,见图6)。同时,当主射流流动达到平衡时,射流进出口的压差增大,使得射流流速增大,因而射流流量增大,射流相对流量也就增大;而当射流角度大于90°时,随着射流角的增大,射流进出口的压差也是增大的,流速增大,但射流有效流通面积则是减小的,面积减小的影响要大于流速增大的影响,射流流量减小,因此与90°相比,射流相对流量也就要小。
为了定量比较这两因素对喉道控制的作用的显著

表2 射流相对流量Table 2 Relative injection mass flow rate

图6 马赫数和静压分布Fig.6 Mach number and static pressure distribution
2.3 喉道面积控制效率的比较
为了进一步比较射流控制效果的优劣,即能以最少的射流流量实现尽量大的喉道面积控制范围。图7给出了喉道面积控制效率(KTAC)随SPR和α的变化情况。从图7可看出,在本文计算的工况下,α=150°、SPR=1时的KTAC是最高的,达到了5.2;角度越大,KTAC越大,这与文献[2]的结论相一致。但随SPR的增大,KTAC则是减小的,这是因为虽然通过增大SPR可使得RTAC增大,但射流相对流量也在增大,两者随SPR的增大速度并不一致,射流相对流量增大速度要大于RTAC的增大速度。所以,SPR增大时,KTAC减小。
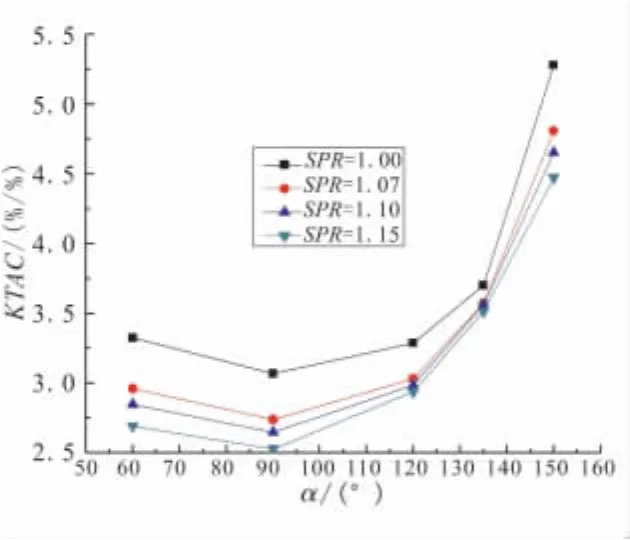
图7 KTAC随SPR和α的变化Fig.7 KTAC vs SPR and α
2.4 射流角度和总压对喷管性能的影响
图8给出了总压恢复系数σ随SPR和α的变化。由图8可看出,SPR越大,σ越小;随着α的增大,σ先减小后增大,在120°时最小。结合图3可知,喉道面积控制范围的增大,也意味着流动损失的增大,所以σ减小。

图8 总压恢复系数σ随SPR和α的变化Fig.8 Coefficient of the total pressure recovery σ vs SPR and α
图9给出了不同SPR、不同α下射流出口附近马赫数分布和流线图。从图9很明显地看出,α<90°时,只在射流缝出口前缘有一个很小的漩涡(图9(a));而当α>90°后,在射流缝出口附近前部和后部分别出现了大小不同的2个低速漩涡(图9(b)、(c)),尤其是后部的漩涡,其范围较大,迫使主流向中间偏转,使得喷管有效喉道面积减小,这是射流控制喉道面积减小的原因,但这也会使流动损失增大。所以,总压恢复系数越小。图9(c)与(b)相比,其漩涡明显较小。这是因为 α =150°时的 W·jet比 α =135°时的 W·jet少很多,其引起的漩涡也就要小。所以,其总压恢复系数有所增大。

图9 马赫数分布云图和流线Fig.9 Mach number distribution and stream line
3 结论
(1)射流角度和射流总压两者对气动喉道面积控制范围都有显著影响。在本文计算的工况下,喉道面积控制范围最大值出现在α=120°、SPR=1.15时,其值为24.53%。
(2)射流角度越大,喉道面积控制效率越高。在射流角度一定的情况下,射流总压增大,喉道面积控制效率减小。在本文计算的工况下,KTAC最大值达到了5.2,对应的 α =150°、SPR=1。
(3)喉道面积控制范围增大,喷管总压恢复系数减小。
[1] Deere K A.Summary of fluidic thrust vectoring research conducted at NASA Langley research center[R].AIAA 2003-3800.
[2] Miller D N,Catt J A.Conceptual development of fixed-geometry nozzle using fluidic injection for throat area control[R].AIAA 95-2603.
[3] Kenrick A Waithe,Karen A Deere.Experiment and computational investigation of multiple injection ports in a convergent-divergent nozzle for fluidic thrust vectoring[R].AIAA 2003-3802.
[4] 额日其太,李喜善,王强.轴对称喷管喉道面积射流控制数值模拟研究[J].推进技术,2010,31(3):361-365.
[5] 邹欣华,王强.带喉道注气的轴对称收扩喷管内流场计算研究[J].航空动力学报,2009,24(9):2078-2084.
[6] 王庆伟,刘波,王如根.二元喷管气动喉道控制的数值模拟[J].航空学报,2009,30(2):226-231.
[7] 郭飞飞,王如根,夏钦斌,等.射流角度对固定几何结构二元喷管气动喉道的影响[J].空军工程大学学报(自然科学版),2010,11(3):26-29.
[8] 韩景,额日其太.带有辅助注气的喷管喉道面积控制方法研究[J].航空兵器,2011,5(10):47-50.
[9] 王全,王强.激波诱导二元矢量喷管内流特性数值研究[J].航空动力学报,2006,21(4):681-685.
[10] 张相毅,王如根,徐学邈,等.双股气流对流体控制矢量喷管的影响[J].航空动力学报,2007,22(9):295-298.
[11] 阎超.计算流体力学方法及应用[M].北京:北京航空航天大学出版社,2006:168-185.
[12] 师义民,徐伟,秦超英,等.数理统计[M].北京:科学出版社,2009:159-164.

