天基发射远程拦截组合机动路径规划①
闫循良,张金生,孙凌逸,2,廖守亿,王仕成
(1.第二炮兵工程大学,西安 710025;2.第二炮兵驻航天四院军代室,西安 710025)
0 引言
随着卫星成为未来战争中获取制信息权的关键,摧毁敌方的卫星系统将是破坏敌方天基信息网和C4ISR系统的最直接手段[1-2]。与地基、空基等反卫星武器相比,天基动能拦截方案具有更明显的优势,对控制和利用空间有着十分重要的战略意义[2]。
在天基远程拦截任务规划过程中,必须设计满足任务要求和约束的可行发射方案、发射参数,实现天基平台与拦截器的组合机动路径规划。
目前,已公开文献往往未考虑天基平台,只研究单一航天器的路径规划和轨道设计问题[3-8]。初始研究常假设发动机按冲量方式工作,将远程导引路径规划转化为多约束最优控制问题进行分析和解决。Prussing[3]研究了时间固定的最优冲量轨道交会和拦截问题,并进行了多种路径约束的分析和仿真。Kara[4]基于主矢量理论发展了一种最优冲量交会路径规划的迭代算法。Ossama[5]采用遗传算法研究了轨道转移路径规划问题。Luo[6]将混合遗传算法应用于冲量交会调相特殊点变轨路径规划,得到了有参考价值的仿真结果。为了获得发射时机和参数,Petropoulos[7]提出了一种较有效的Shape-Based搜索算法,该算法通过指数函数来描述探测器的飞行轨迹,从而进行发射时机搜索。这些研究均只选择脱离平台后的航天器作为对象,进行轨道机动路径规划的研究。事实上,平台姿、轨机动策略和发射方案将直接影响拦截器的作战能力[9-11],路径规划必须考虑发射技术以及平台机动的影响。考虑到卫星系统大都是由多颗卫星组成的星座,攻击其中的一两颗卫星并不足以破坏整个系统的功能。因此,需要同时考虑单/多目标天基发射拦截问题。
基于冲量假设并考虑天基发射,本文对单/多目标天基发射远程拦截中涉及的发射技术和组合机动路径规划策略进行研究。其实质为一类受发射参数制约的多约束多参数路径优化问题。由于发射窗口、发射姿态参数与路径规划相互影响制约,在路径规划中必须将发射参数作为决策变量进行优化。
1 天基发射远程拦截分析
选择合理的发射方式、发射窗口、发射姿态等诸元是实现天基发射和空间拦截的前提。
(1)发射方式选择
直接点火加速推进和投放发射是目前通常采用的近地轨道发射方式。拦截器直接点火会对平台产生冲击和烧蚀,不利于平台的安全性。无动力投放发射的初始变轨速度要由拦截器自己来建立,需要很大的能量,对整个飞行过程不利。动力投放发射由平台提供初始变轨速度,并建立发射状态。综合考虑目前的机械力、电磁、压缩空气和燃气弹射等动力投放方式知,燃气弹射利用了小体积推进剂燃烧产生的燃气,能提供较大能量,是一种最为有效的投放方式。本文选择燃气弹射方式发射,并假设弹射速度为常值。
(2)发射窗口及姿态需求分析
在空间拦截中争取有利的发射时机非常重要。接到作战任务后,如何规划发射时机是天基发射一个关键问题。根据不同的发射任务,就地发射、等待时机发射或平台机动后再发射是3种不同的发射方案。发射拦截器时,需要建立起平台的姿态,才能保证拦截器获得合适的初始变轨速度,并以较少的能量完成拦截。若由拦截器去建立初制导姿态,会额外消耗较多的拦截器能量,影响其作战范围。因此,进行发射时,需要首先规划出发射所需姿态,该姿态可通过平台快速大角度姿态机动获得。
2 非线性冲量最优拦截问题
2.1 最优拦截模型
考虑发动机推力和J2摄动,航天器冲量变轨动力学方程可描述为如下Cowell形式:

相关参数具体定义可参见文献[10]。对于要求快速响应的空间拦截而言,选择优化变量为
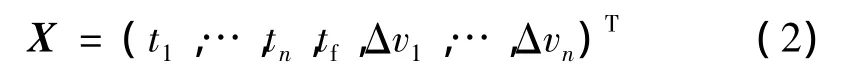
选取拦截时间最短作为价值函数,即

拦截初始条件为 t0、r0、v0,终端条件 tf、rf待定。
为了确定上述问题的解,需要求解一个在时间区间[t0,tf]的最优控制问题,并满足下述冲量施加约束、终端约束、变轨时刻约束及路径约束:

其实质为一多约束、多参数优化问题,可采用相应优化算法进行求解。
2.2 串行优化求解策略
为了提高收敛速度和算法的鲁棒性,采用串行优化策略求解摄动优化问题,具体流程见图1。
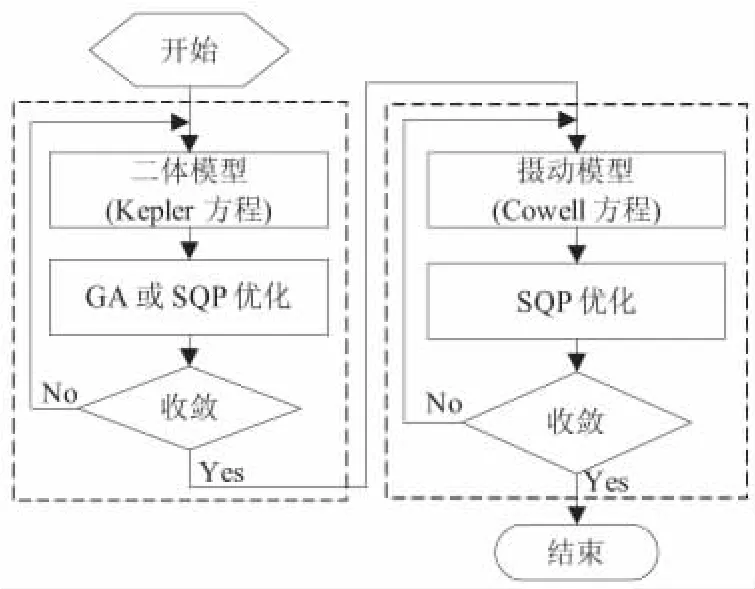
图1 考虑摄动的时间最短拦截串行优化策略Fig.1 Serial optimization strategy for minimum time interception with perturbations
3 单目标拦截组合机动路径规划
3.1 单目标拦截组合机动分析
首先做如下假设:(1)平台可进行不超过1次变轨;(2)设发射装置固定在平台轴线方向,和平台之间无相对运动;(3)平台能提供任意所需的发射姿态,且不考虑姿态机动的燃耗;(4)发射装置及发射过程是理想的,即不考虑发射过程中的相互干扰;(5)平台在完成发射后,能重新回到原初始轨道继续待命。
天基发射及单目标轨道拦截过程如图2所示。具体过程如下:
(1)平台t0时刻接到作战任务,在原轨道待命;
(2)t1时刻,平台变轨,进入转移轨道,变轨冲量为Δv1;之后,通过姿态机动建立发射状态;
(3)t2时刻,平台以Δv2的发射速度将拦截器发射,设拦截器的离开速度为v2+;
(4)以v2+为初始速度,拦截器进行(n-2)次冲量变轨,并最终于tf时刻实现对目标的拦截。
选取合适的优化变量和价值函数,即可采用非线性规划技术进行优化求解,得到最佳发射诸元及最优飞行轨迹。由于发射参数与路径规划相互影响制约,因此在路径规划过程中必须将发射诸元作为决策变量进行优化。该拦截过程考虑了平台的变轨。事实上,平台机动后发射拦截器,扩大了拦截器的杀伤区,增强了其作战能力。

图2 天基发射及单目标轨道拦截示意图Fig.2 Space launch and single-target interception diagram
3.2 单目标拦截组合机动分析
根据上述分析,建立非线性规划模型如下:

其中,各变量和表达式的具体形式如下:
(1)优化变量及目标函数
优化变量同式(2),优化目标为式(3)。
(2)运动方程约束
变轨过程中考虑J2摄动的影响,平台、拦截器和目标的运动均满足式(1)。
(3)时间约束
变轨时刻满足以下约束条件:
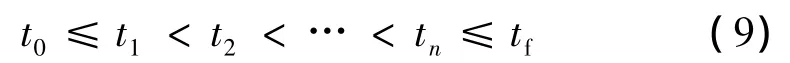
考虑变轨前的姿态调整准备,因此要求任意2次冲量作用时刻间隔大于一定值tint,即
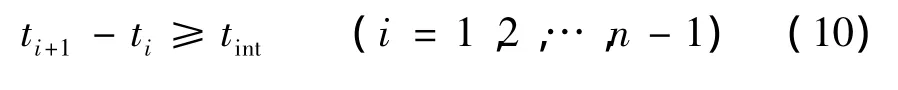
(4)变轨能力(燃料)约束
平台提供的单次冲量大小上限为Δvpmax。考虑到拦截器初始变轨速度Δv2由平台提供,而该发射速度取决于发射分离机构,故设Δv2大小一定,通过施加约束来满足该限制,即

拦截器提供的单次冲量大小上限为Δvkmax,提供的冲量大小总量约束为
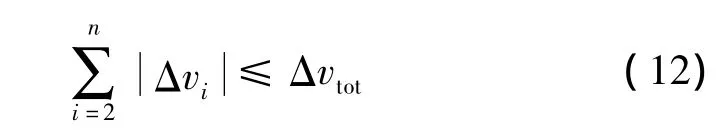
(5)拦截终端状态约束
设rcf、rtf分别为拦截器和目标的终端位置矢量,则有

(6)轨道内点路径约束
考虑到发射完成后,平台需要返回到原轨道,因此有最小或最大半径内点路径约束:
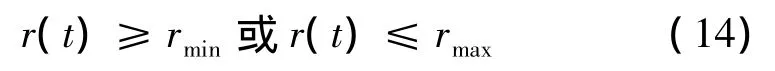
其中,rmin、rmax分别为允许的最小、最大地心距。
设平台在地心惯性系的俯仰角和偏航角分别为α和 β,有 α∈[-0.5π,0.5π],β∈[- π,π];令 Δv'=sqrt(+),由 sinα = Δv2z/Δv2,sinβ = Δv2x/Δv',cosβ=Δv2y/Δv',即可得到发射时刻的平台姿态角(α,β)。最佳发射时刻为t2,发射速度为Δv2。
3.3 仿真及分析
仿真条件:平台初始轨道要素Ec0=(6 871 km,0.001,97.38°,50°,20°,10°),目标初始轨道要素 Et0=(26 571 km,0.000 1,55°,60°,30°,0°)。其他参数:t0=0,tint=20 s,Δvpmax=2 km/s,Δv2=1 km/s,Δvkmax=3 km/s,Δvtot=8 km/s,rmin=6 471 km,rmax=7 171 km。仿真中,进行参数和模型的归一化处理[10]。
针对不同的冲量数量,采用串行优化策略进行多次优化。表1给出了时间最短拦截的优化解。考虑到平台进行1次冲量变轨,并提供1次发射冲量,故拦截器的冲量变轨次数为(n-2),n为仿真中的冲量数。以3冲量为例,平台首先进行待命,在2 914.27 s进行变轨,变轨冲量大小为2 km/s;之后,在最佳发射窗口5 103.83 s以大小为1 km/s的速度将拦截器发射,发射角为(35.99°,-19.39°);拦截器在 5 416.31 s进行1次变轨,最终在10 151.61 s以4.023 2 km/s的拦截速度实现拦截。受轨道内点约束限制,平台机动段近地点和远地点地心距分别为6 749.2、7 171 km,发射地心距为6 897.3 km。
分析表1数据知,随着冲量数目增加,拦截时刻减小。对于拦截器机动1、2次的情况,约束Δvkmax起作用,平台及拦截器的单次冲量大小均达到了额定最大值,这也体现了时间和能量之间的矛盾;对于机动3次的情况,Δvkmax和冲量总和约束Δvtot均起作用。拦截脱靶量均为1 m量级,主要是由J2摄动和终端约束计算误差所引起的,考虑到碰撞拦截的要求,因此需进行拦截器末制导的分析和研究。实际拦截中往往要求拦截速度较大,仿真中,通过增加冲量数量可使得拦截速度增大[10]。
多次仿真表明,串行优化求解策略的收敛率为100%;若直接采用摄动方程求解,单次求解平均耗时为串行求解策略的3倍以上[10]。可见,本文的串行求解策略大大提高了规划算法的收敛速度。
对比表1中发射窗口和发射姿态数据可知,不同的任务要求对应完全不同的最佳发射窗口和发射角。由最优解的性质可知,任意改变发射窗口和发射角,均无法获得与原最优解一致的结果,其结果均为次优解,甚至不收敛解。即在规定的时间和燃料要求下,拦截器并不能够完全保证对目标实现拦截。可见,平台发射姿态对任务燃耗和飞行覆盖范围具有较大的影响,发射前平台必须进行大角度姿态机动。作者在文献[8]、[10]中对可行的发射窗口和发射角范围进行了详细的分析讨论。

表1 单目标时间最短拦截优化结果Table 1 Minimum time optimization results for single-target interception
图3给出了相应的空间轨迹变化曲线,图4给出了变轨过程中拦截器的地心距和速度变化曲线。
可见,平台经过较长的等待阶段后才进行机动。对于拦截器进行2、3次机动的情况,平台无待命阶段,初始时刻即进行机动。可见,需要根据具体任务确定发射时机并做出平台是否机动的决定。
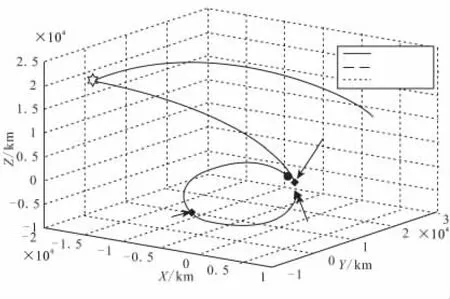
图3 单目标拦截的空间轨迹曲线Fig.3 Trajectory of single-target interception
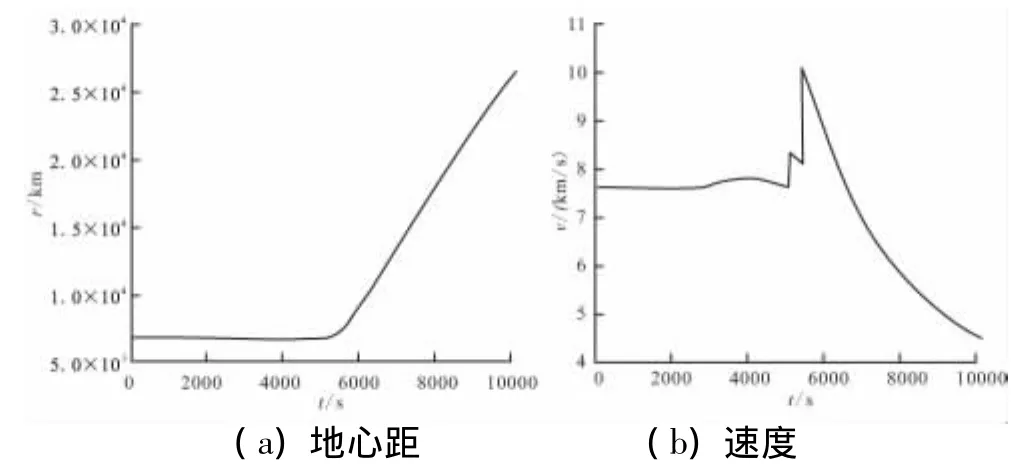
图4 地心距及速度变化曲线Fig.4 Geocentric distance and velocity curves
4 多目标拦截组合机动路径规划
在战场上目标并不是逐一单独出现的,当同时出现多个目标的时候,空间武器系统就必须具备摧毁多个目标的能力。考虑目标的智能性和机动性,应该尽可能地同时摧毁多个目标,使得目标没有规避机动的时间,从而提高命中概率,争取战争的胜利。下文研究是在该战争背景下进行的,即对敌方的1个卫星监视系统进行攻击,要求在一定的时间间隔之内击毁敌方2颗卫星。
4.1 多目标拦截组合机动分析
假设:(1)平台和拦截器均可进行不超过1次变轨;(2)平台变轨与拦截器发射在同一时刻进行,即平台变轨冲量和发射速度近似合成为第一次变轨冲量;(3)敌方目标在同一轨道运行。其他与4.1节一致。天基发射及星座多目标轨道拦截过程见图5。
具体变轨策略:平台在初始轨道1运动,已知t0时刻,平台位置为p0,目标星1的位置为s10,目标星2的位置为s20;平台经过等待,根据任务规划指令,在t1时刻机动变轨至轨道2继续等待,于t2时刻发射拦截器1,于t3时刻发射拦截器2,拦截器经过变轨,最终分别在 t1f、t2f时刻,位置 s1f、s2f分别实现对目标星 1、2 的拦截。
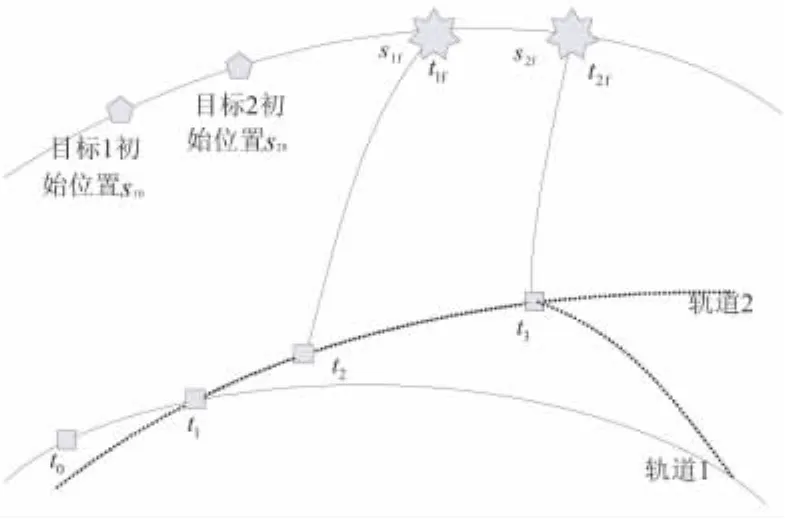
图5 天基发射及星座拦截示意图Fig.5 Space launch and constellation interception diagram
4.2 多目标拦截路径规划模型
非线性规划模型同式(8)。
(1)优化变量及目标函数
根据上述组合机动分析,选择优化变量为
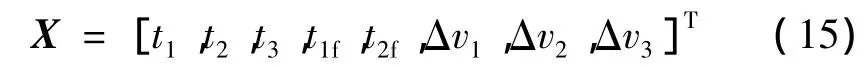
其中,拦截器1、2提供的单次冲量分别为Δv21和Δv31,分离机构提供给拦截器1、2的初始变轨速度均为Δvlau,并满足:

为了保证拦截时间极小化,作战指标为拦截时间最小,即
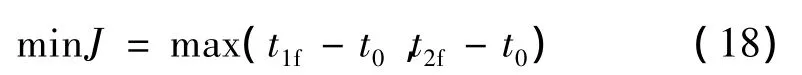
(2)时间约束
考虑到2次拦截的时间间隔要求,有

式中 tc为允许的最大拦截时间间隔。
变轨时刻满足以下约束条件:

同时要求任意2次冲量作用时刻满足式(10),对应 i=1,2。
(3)变轨能力(燃料)约束
平台、拦截器提供的单次冲量大小,以及分离机构发射速度约束与前述单目标情况相同。
(4)终端状态约束
若要实现对卫星星座中2颗星的拦截,终端状态需要满足:

式中 rc1f、rc2f分别为拦截器1、2终端时刻位置矢量;rs1f、rs2f为目标星1、2终端时刻位置矢量。
此外,运动方程约束满足式(1),轨道内点约束同式(14)。
4.3 仿真及分析
仿真条件:平台初始轨道要素Ec0=(6 871 km,0.001,65°,55°,20°,10°),异面椭圆轨道星座目标卫星轨道要素 Et0=(7 471 km,0.011 7,63.4°,60°,fsi),i=1,2。目标1的初始真近点角fs1=20°,目标2为fs2=80°。其他参数:t0=0,tint=20 s,Δvpmax=2 km/s,Δvlau=1 km/s,Δvkmax=3 km/s,tc=50 s,rmin=6 471 km,rmax=7 171 km。
采用串行优化策略进行求解,结果见表2。由表2可知,平台在轨道1经过544.45 s等待,以2 km/s冲量变轨至轨道2,并于1 901.83 s发射拦截器1,发射角为(-16.10°,-86.31°),于5 115.67 s发射拦截器2,发射角为(29.78°,-119.53°),并在 5 857.43 s和5 882.63 s分别实现对目标1和2的拦截,拦截相对速度 vint1及 vint2较大,分别为 2.131 km/s和4.344 7 km/s;拦截时间间隔为 25.2 s,大大缩短了敌方卫星规避机动的时间,提高了命中概率。拦截消耗总的特征速度为7.202 2 km/s,满足燃料限制。
可见,采用本文的发射和规划策略,可在规定的时间差内完成对多个目标的最短时间拦截。改变最大拦截时间间隔tc进行多次仿真发现,该参数对优化结果具有较大影响,间隔时间越小,最终拦截时刻越小,耗能越大[10]。
考虑弹射速度,拦截器1消耗自身能量仅为0.202 2 km/s,而拦截器2消耗自身能量为3 km/s,这是由多种因素造成的,包括发射时间和位置、目标位置,拦截器1发射较早,因而具备较长的拦截时间,而拦截器2发射较晚,拦截时间较短,轨道改变较大。因此,针对复杂战场形势,需要合理规划发射方案和发射参数。前文分析中的假设使得问题建模和仿真简化,但平台变轨和拦截器发射并不是在同一时刻进行的,拦截器亦可进行多次变轨以减小燃耗和拦截时间,所以需要进一步讨论和分析。本文的研究方法和结果可 为后续的工作提供思路和参考。

表2 多目标时间最短拦截优化结果Table 2 Minimum time optimization results for multi-targets interception
5 结论
(1)所提出的发射方案和规划策略,可有效实现单/多目标天基发射远程拦截任务,能够在多种约束和摄动情况下,实现最优组合机动飞行路径规划,为远程拦截初制导问题提供有价值的参考。
(2)平台发射姿态对任务燃耗和飞行覆盖范围具有较大的影响,发射前平台必须进行大角度姿态机动;发射窗口将会影响飞行任务的时间和燃料消耗,需要根据具体任务在立即发射、等待发射或机动发射中进行合理选择;对于文中的单目标时间最优拦截而言,根据燃料的不同,平台存在原轨道等待机动后发射和直接机动后发射两种情况。
(3)优化求解时,将二体问题的解作为摄动解的初始点,该串行求解策略可显著提高路径规划算法的收敛速度和鲁棒性;对冲量变轨时刻的归一化处理能有效的提高优化性能;对于多冲量变轨,冲量作用时间间隔tint约束对优化结果有一定的影响;平台机动的最大半径约束rmax对优化结果的影响也较明显;多目标拦截的时间间隔对优化结果具有较大影响,间隔时间越小,最终拦截时刻越小,耗能越大。
[1] David Wright,Laura Grego,and Lisbeth Gronlund.The physics of space security[R].American Academy of Arts and Sciences,2005.
[2] 冯志刚,方昌华.世界各国反卫星策略综述[J].中国航天,2006(3):38-41.
[3] Der-Ren Taur,John E Prussing.Optimal impulsive timefixed orbital rendezvous and interception with path constraints[J].Journal of Guidance,Control and Dynamics,1995,18(1):54-60.
[4] Kara Z M,Arzelier D,Louembet C.Mixed iterative algorithm for solving optimal impulse time-fixed rendezvous problem[C]//AIAA Guidance,Navigation,and Control Conference.Toronto,Ontario Canada,2010.
[5] Ossama Abdelkhalik,Daniele Mortari.N-impulse orbit transfer using genetic algorithms[J].Journal of Spacecraft and Rockets,2007,44(2):456-459.
[6] Luo Ya-zhong,Li Hai-yang,Tang Guo-jin.Hybrid approach to optimize a rendezvous phasing strategy[J].Journal of Guidance,Control and Dynamics,2007,30(2):185-191.
[7] Petropoulos A E,Longuski J M.Shape-based algorithm for automated design of low-thrust,gravity-assist trajectories[J].Journal of Spacecraft and Rockets,2004,41(5):787-796.
[8] Yan Xun-liang,Chen Shi-lu,Xu Min,Qian Yu.Mission planning of long distance guidance for space rendezvous[C]//ICIECS,2009:421-425.
[9] 张泽明,姜毅,傅德彬.天基发射与载人登月初探[J].中国工程科学,2006,8(10):37-41.
[10] 闫循良.基于空间发射的组合机动路径规划研究[D].西安:西北工业大学,2011.
[11] 赵瑞安.空间武器轨道设计[M].北京:中国宇航出版社,2008.

