铝蜂窝异面压缩吸能特性实验评估
(中南大学 交通运输工程学院 轨道交通安全教育部重点实验室,湖南 长沙,410075)
铝蜂窝是一种规整的二维周期排列复合结构。因其质量轻、吸能能力强、安装方便,现已广泛应用于吸能相关领域中。六边形铝蜂窝是目前为止最为普遍的一种,其异面加载与共面加载所体现的吸能性能差异明显[1]。国内外针对蜂窝吸能特性开展了很多的研究工作,就其冲击作用下的异面力学行为取得了相对可观的研究成果。Wierzbicki[2]首先研究了金属蜂窝的异面压缩力学性能, Gibson等[3]对蜂窝的结构与性能进行了详细阐述;Wu等[4−6]研究了蜂窝在准静态与低速冲击条件下的力学特性;Yamashita等[7]采用数值模拟与实验相结合的方法,分析了不同蜂窝结构的力学特性,得到了更广泛的研究成果。国内主要针对其理论模型及应用开展研究。Sun等[8]研究了规则蜂窝异面动态冲击平台力;王闯等[9]研究了铝蜂窝结构的冲击动力学性能,并利用简化的“Y”形胞元模型开展了与实验对应的数值模拟研究;王永宁等[10]基于壳单元建立了铝蜂窝大变形有限单元模型,对受异面动态加载下的铝蜂窝进行了数值模拟;罗昌杰等[11]基于Y型折叠单元推导了蜂窝的理论平台力。这些研究主要集中在蜂窝特性本身,且主要关心其力学属性,并未深入地比较吸能的相关特性。在此,本文作者基于准静态实验和台车动态撞击实验,对不同规格铝蜂窝试件开展吸能能力特性评估。
1 蜂窝结构特点及其吸能特性
商用铝蜂窝结构示意图如图1所示。其中,L为共面长度、W为宽度、T为异面厚度,t为铝箔厚度、l为边长、h为边高、θ为内仰角。对于正则六边形,θ=30°,h=l。商用蜂窝受生产工艺影响,黏接成型后使得单胞6边中有2边为双倍壁厚,其几何形态如图1(b)所示。
表观密度是描述多胞材料物理特性的最重要参数。经几何推导[9],考虑厚度所占部分的面积,可得正则蜂窝的表观密度*ρ:
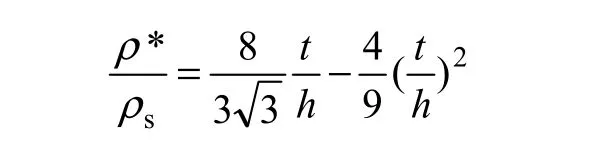
式中:sρ为多胞结构母体材料的密度;t/h为结构的厚跨比。
蜂窝的异面压缩力学性能与吸能能力明显比共面压缩的优,在缓冲与吸能领域中多利用异面来承受冲击载荷。其压缩变形主要经过线弹性、初始塑性坍塌、渐近屈曲、密实化4个阶段[1,3],如图2所示。渐近屈曲段有稳定的平台力,是考察蜂窝材料性能的最主要区段。
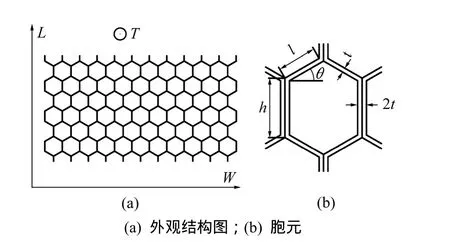
图1 商用铝蜂窝结构示意图Fig.1 Honeycomb structure

图2 蜂窝材料吸能特性Fig.2 Energy absorption property of honeycomb
2 异面压缩性能评估指标
优良的蜂窝吸能产品需同时满足轻质、高能、平台区稳定、波动小的要求。其吸能特性的常用评定指标分为力学指标与能量指标2类。考核不同结构形式蜂窝的吸能特性需采用比值形式,才能避免因引入体积量而引起的基准偏差,评估指标主要有平台强度、比载荷、质量比吸能、体积比吸能[12]。同时,能量吸收图也是评定不同材料吸能特性的好方法[13−14]。
(1) 平台强度σmean。通过对载荷位移历程中的平台区段(图2中的CD段)求均值得到,主要反映结构的整体承载水平。由于蜂窝结构平台区段载荷比较稳定,且压缩率均可达到70%以上,研究平台强度取压缩率为 33%~66%区段对应的平均平台强度作为该蜂窝的平台强度。
(2) 比载荷Fs。

式中:F为载荷;A为试件受压面面积。蜂窝材料受表观密度影响很大,比载荷可很大程度反映不同表观密度蜂窝的吸能能力。由于蜂窝平台区长度远远大于初始坍塌区与密实区的长度,因此,比载荷由计算得到。
(3) 质量比吸能Em。
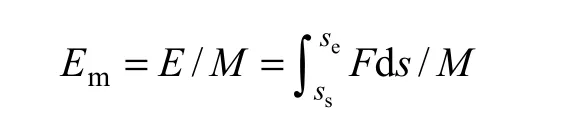
式中:E为蜂窝总吸能量;M为蜂窝芯块的总质量;ds为位移增量;Se与Ss分别对应受压方向的位移起点与位移终点。不同密实程度的蜂窝总吸量不同。直接将密实段的应变作为位移终点,比较结果并不是在同一基准线上得到。本文考虑的铝蜂窝结构吸能量是指从初始撞击时刻至结构初始密实时刻为止,铝蜂窝所吸收的能量,对应图2中的AD段。
(4) 体积比吸能Ev。当因安装空间有限等受体积量约束时,通常用体积比吸能表征结构有效破坏长度单位体积内吸收的能量,Ev=E/V,式中,V为蜂窝芯块的体积。
δk的值越大表明方案ak越好,将第七步中得到的δk按从大到小的顺序进行排序得到的顺序,就是最终的方案的排序,从而可以选出最佳方案。
(5) 能量吸收图。能量吸收图由Maiti等[13]提出,多用在泡沫塑料或泡沫铝的包装设计与抗冲击优化中,它用以表征缓冲材料所承受的应力和吸收的能量之间的关系,可由缓冲材料受压时的应力应变曲线来构建。Wang[14]将其应用于瓦椤纸蜂窝性能评估。肩点是多孔材料能量吸收图的典型特征,可以反映不同密度材料不同结构型式的缓冲材料的最佳吸能性能。本文通过构建能量吸收图来表征铝蜂窝的设计应力与其单位体积吸收能量之间的对应关系。
3 实验方法与样品
3.1 实验方法
评估蜂窝结构吸能特性通常采用准静态实验与动态实验2种方法。准静态实验在专用的INSTRON万能材料力学性能实验机上进行。
准静态实验可直接得到试件的力−位移(F−L)曲线,忽略摩擦力与蜂窝孔壁惯性效应所消耗的微小能量,以初始密实时刻为积分终止点,F−L曲线与坐标轴所围面积即为蜂窝试件所吸收的能量。
动态实验方案以落锤为主,因引入了落锤重力加速度,需排除重力作用附加冲量的影响;本文的动态实验采用水平台车撞击方案,从而避免输入加速度对实验结果的影响,其实验系统见文献[15]。台车动态撞击实验通过将撞击试件固定于运动台车前端,加速至预定速度后释放,台车与牵引装置分离后撞向刚性墙面,测试刚性墙撞击力−时程(F−t)响应。实验过程综合使用了瞬时速度测量、同步触发、高速摄像动态捕捉等设备与技术,撞击前后蜂窝形态如图3所示。

图3 蜂窝台车撞击实验前后形态Fig.3 Honeycomb performances before and after dynamic impact experiment
通过高速摄影动态捕捉的撞击图像关键帧序列,提取位移−时间(L−t)曲线;结合同步触发力−时程曲线,可得到力−位移曲线,进而积分得出蜂窝的吸能量。
3.2 样品参数
4种规格的正则商用铝蜂窝产品(h=l)如表1所示。母体材质均为 Al 5052H18,铝箔材料的弹性模量为Es=69 GPa,泊松比ν=0.33。准静态实验加载速度通常为50~500 mm/min,本文选用100 mm/min。动态冲击实验因各试件吸能能力不同,对应的冲击速度也不同。实验前测定各试件的初始几何尺寸与质量。4个指标均为单位化的量,考虑到准静态实验条件的限制,采用相对较小的试件,其W×L×T为200 mm×100 mm×120 mm;动态冲击实验试件W×L×T为 200 mm×400 mm×240 mm。各结构参数及动态撞击初始速度V0如表1所示。

表1 铝蜂窝的结构参数Table 1 Parameters of honeycomb structure
4 铝蜂窝材料吸能特性评估
4.1 实验结果
准静态与台车撞击实验所得的平台强度、比载荷、质量比吸能和体积比吸能结果见表2。
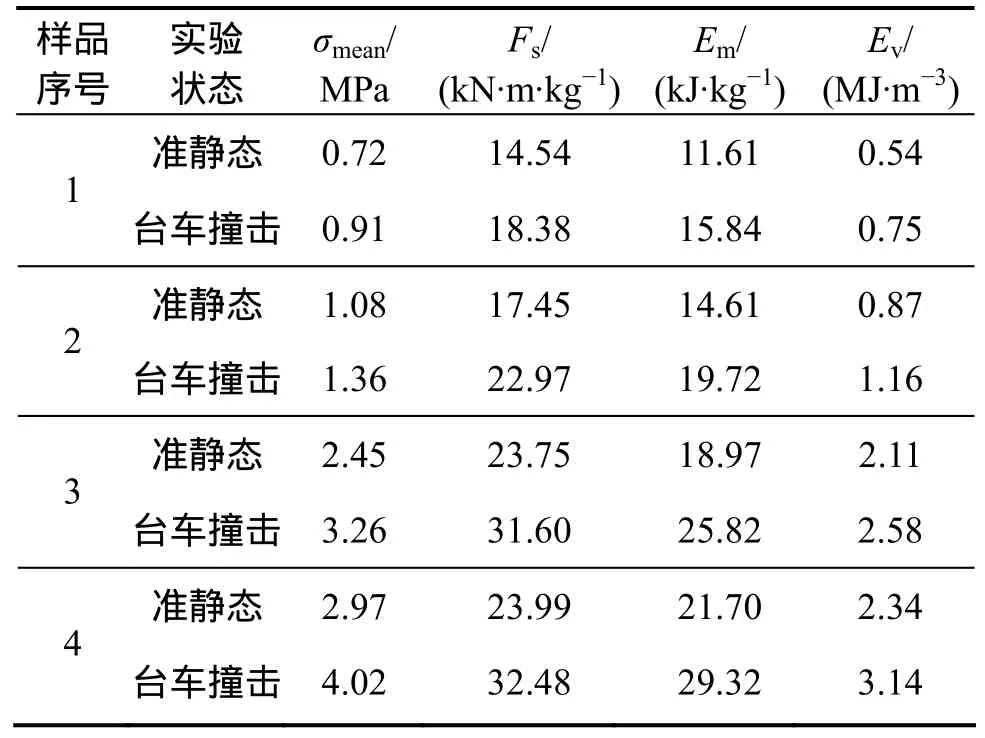
表2 准静态与台车撞击实验结果Table 2 Results of quasi-static and dynamic experiments
准静态实验与台车动态撞击实验的F−L曲线如图4所示。
4.2 结果分析
为方便比较,选择厚跨比为 0.012的准静态实验结果为基准值,将表2结果进行归一化。力学特性与能量特性随厚跨比变化趋势及拟合曲线如图5和图6所示。
由图5和图6可见:平台强度、比载荷、质量比吸能、体积比吸能均与厚跨均比成幂次变化;比载荷与质量比吸能的幂次均为0.67,体积比吸能的幂次为1.48,而平台强度的幂次却略有差异,分别 1.57和1.49,均值为 1.53。平台强度与体积比吸能的幂指数大于1,而比载荷与质量比吸能幂指数小于1,因此,随厚跨比增大,平台强度与体积比吸能增幅增大,而比载荷与质量比吸能增幅较缓。
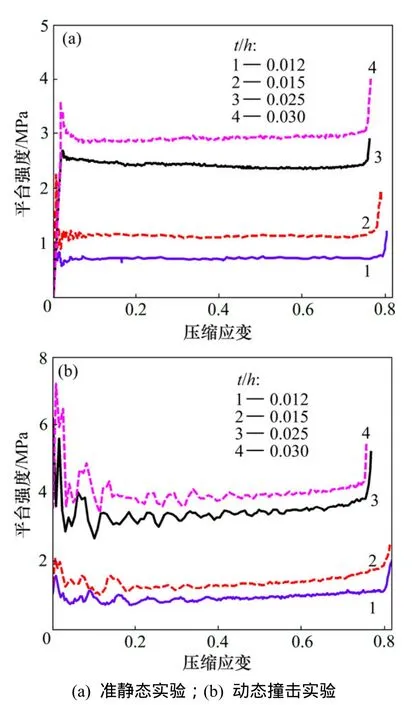
图4 准静态与动态撞击F−L曲线Fig.4 F−L curves of quasi-static and dynamic experiment

图5 准静态与动态力学特性对比Fig.5 Comparison of mechanical property between quasi-static and dynamic experiments
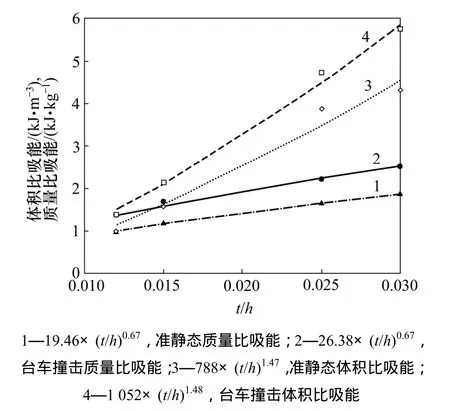
图6 准静态与动态比吸能对比Fig.6 Comparison of SEA between quasi-static and dynamic experiments
动态撞击与准静态压缩相比,各规格蜂窝的平台强度、比载荷、质量比吸能、体积比吸能均有所提升,这反映在幂函数系数的变化上,动态撞击时平台强度、比载荷、质量比吸能、体积比吸能的拟合幂函数系数分别为静态条件下的1.78,1.32,1.35,1.33倍,除平台强度的系数稍高外,其余三者较为接近,平均为1.33倍。
4.3 能量吸收图
根据不同蜂窝结构的应力−应变曲线,将应力σ以下每条曲线的面积取为该蜂窝单位体积吸收的能量,并用标准固体基材弹性模量Es进行标准化[3,16]。准静态的压缩速度为100 mm/min,各次实验的应变率均为10−2s−1,其能量吸收曲线如图7所示。
动态撞击条件下,结构的冲击速度不相同,得出的能量吸收图有所偏差,但因其均属低速撞击范围,应变率为16~26 s−1,均处在同一量级水平,且相差不大,因而本文忽略低速条件下因台车撞击速度不同而引起的应变率效应。动态撞击实验所得的能量吸收曲线如图8所示。
将不同蜂窝胞壁厚跨比所对应的能量吸收曲线的肩点连接起来,形成最佳的设计曲线,即可构建出设计应力σp与单位体积吸收能量之间的关系。准静态和动态冲击条件下,蜂窝能量吸收图中肩点的线性方程为:

图7 蜂窝准静态实验能量吸收曲线Fig.7 Energy absorption curvesat quasi-static state
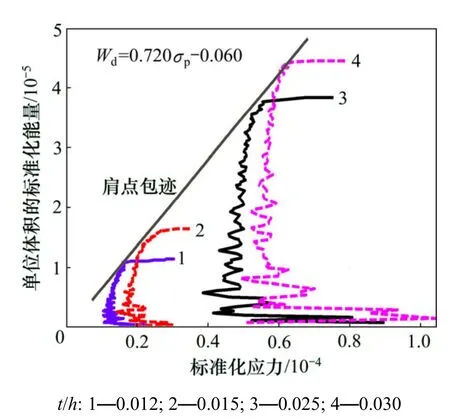
图8 蜂窝动态撞击能量吸收曲线Fig.8 Energy absorption curve at dynamic state
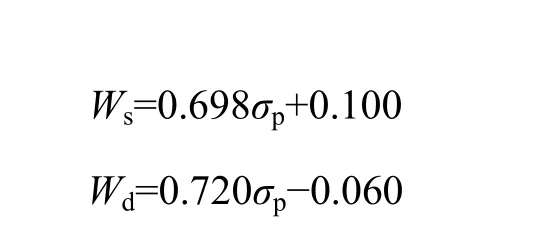
其中,Ws与Wd分别为准静态与动态条件下蜂窝单位体积吸收的能量。对比2个方程可知:低速条件下,动态系数比准静态的稍大,与前述分析一致。利用 2个方程可实现满足工程能量需求的蜂窝平台强度的反演设计。
5 结论
(1) 对不同规格蜂窝进行准静态与低速台车动态冲击实验发现,在该实验条件下,动态撞击与准静态压缩相比,各规格蜂窝的平台强度、比载荷、质量比吸能、体积比吸能均有所提升,平均提升约33%。
(2) 铝蜂窝的平台应力、比载荷、质量比吸能、体积比吸能均随厚跨比的增大呈幂次增大,比载荷、质量比吸能的幂指数为0.67,平台强度幂次约为1.53,体积比吸能幂次约为1.48;吸能能力随厚跨比的增大而提升,体积比吸能比质量比吸能增加更为明显。
(3) 所绘的准静态压缩与低速冲击蜂窝能量吸收图表征了平台应力与单位体积吸收能量的变化关系,反映了不同厚跨比蜂窝的最优吸能设计点,由系列蜂窝的肩点线性方程表达式可建立设计强度与需求能量间的推算关系,并可高效地反演设计出适合工程实际需求的蜂窝产品。
致谢
感谢中南大学现代分析测试中心力学室提供的准静态实验设备及实验指导。
[1] Lu G X, Yu T X.Energy absorption of structures and materials[M].Cambridge: Woodhead Publishing Limited, 2003:268−278.
[2] Wierzbicki T.Crushing analysis of metal honeycomb[J].Int J Impact Eng, 1983, 2(1): 157−174.
[3] Gibson L J, Ashby M F.Cellular solids: Structures and properties[M].2nd ed.Cambridge: Cambridge University Press,1997: 93−158.
[4] Wu E, Wu S.Axial crush of metallic honeycombs[J].Int J Impact Eng, 1997, 19(3): 439−456.
[5] Zhao H, G Gary.Crushing behavior of aluminum honeycombs under impact loading[J].Int J Impact Eng, 1998, 21(10):827−836.
[6] Hu L L, Yu T X.Dynamic crushing strength of hexagonal honeycombs[J].Int J Impact Eng, 2010, 37(5): 467−474.
[7] Yamashita M, Gotoh M.Impact behavior of honeycomb structures with various cell specifications: Numerical simulation and experiment[J].Int J Impact Eng, 2005, 32(1/2/3/4):618−630.
[8] Sun D Q, Zhang W H, Wei Y B.Mean out-of-plane dynamic plateau stresses of hexagonal honeycomb cores under impact loadings[J].Compos Struct, 2010, 92(11): 2609−2621.
[9] 王闯, 刘荣强, 邓宗全, 等.铝蜂窝冲击动力学性能与数值模拟[J].振动与冲击, 2008, 27(11): 56−62.WANG Chuang, LIU Rongqiang, DENG Zongquan, et al.Experimental and numerical studies on aluminum honeycomb structure with various cell specification under impact loading[J].Journal of Vibration and Shock, 2008, 27(11): 56−62.
[10] 王永宁, 李大永.铝蜂窝异面变形数值模拟[J].中国机械工程, 2006, 17(10): 340−343.WANG Yongning, LI Dayong.Numerical simulations of aluminum honeycomb out-plane deformation[J].China Mechanical Engineering, 2006, 17(10): 340−343.
[11] 罗昌杰, 周安亮, 刘荣强, 等.金属蜂窝异面压缩下平均压缩应力的理论模型[J].机械工程学报, 2010, 46(18): 52−59.LUO Changjie, ZHOU Anliang, LIU Rongqiang, et al.Average compressive stress constitutive equation of honeycomb metal under out-of-plane compression[J].Journal of Mechanical Engineering, 2010, 46(18): 52−59.
[12] 宋宏伟, 范子杰, 虞钢.几类典型耐撞性结构吸能性能的比较[C]//中国汽车工程学会.汽车安全技术.北京:人民交通出版社, 2004: 44−49.SONG Hongwei, FAN Zijie, YU Gang.Energy absorption behavior of several typical crashworthy structures[C]//Society of Automotive Engineers of China.Technologies of Automotive Engineering.Beijing: China Communications Press, 2004:44−49.
[13] Maiti S K, Gibson L J, Ashby M F.Deformation and energy absorption diagrams for cellular solids[J].Acta Metallurgica,1984, 32(11): 1963−1975.
[14] Wang Dongmei.Energy absorption diagrams of multi-player corrugated boards[J].Journal of Wuhan University of Technology: Materials Science Edition, 2010, 25(1): 58−61.
[15] 谢素超, 田红旗, 姚松.车辆吸能部件的碰撞实验与数值仿真[J].交通运输工程学报, 2008, 8(3): 1−5.XIE Suchao, TIAN Hongqi, YAO Song.Impacting experiment and numerical simulation of energy-absorbing component of vehicles[J].Journal of Traffic and Transportation Engineering,2008, 8(3): 1−5.
[16] WANG Zhiwei, E Yuping.Mathematical modeling of energy absorption property for paper honeycomb in various ambient humidities[J].Mater & Design, 2010, 31(9): 4321−4328.

