利用“弦”求解带电粒子在磁场中的运动问题

何琰

(宁波市效实中学 浙江 宁波 305012)

求带电粒子在有界磁场中做匀速圆周运动的时间问题是高考考查的重点内容之一.这类问题的常规解法是,先作出粒子的轨迹圆，应用牛顿第二定律和洛伦兹力公式,再结合图像的几何关系进行求解.然而，当这类问题与极值或临界问题相结合，即要求带电粒子在磁场中运动的最长或最短时间时，情况就会变得复杂，学生往往感到无从下手或走弯路.这时,若能以粒子在磁场中运动的轨迹圆的“弦”为突破口，问题的处理就会简捷得多.笔者结合具体的例子来说明“弦”在解磁场题中的应用.

1 弦与运动时间的关系

情境:半径为r的圆柱形区域内有一匀强磁场，磁感应强度为B，方向垂直纸面向外.一质量为m,电荷量为+q的粒子以初速度v从磁场边界的A点垂直射入磁场，经磁场偏转后,从C点射出，已知粒子的轨迹圆半径R>r，忽略粒子重力，如图1所示.

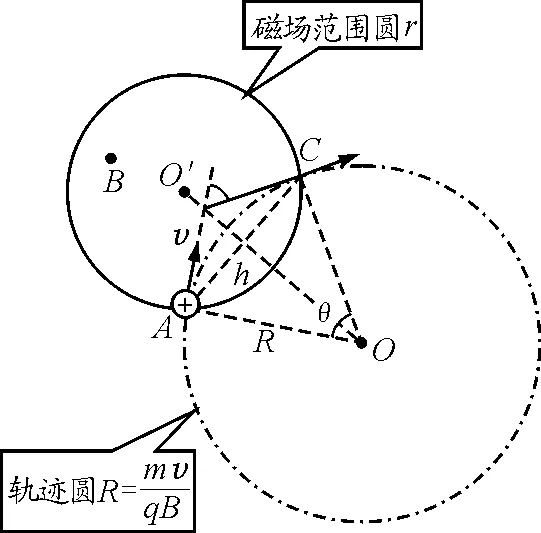
图1

粒子在磁场中运动的时间

(1)

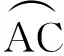
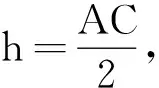
(2)

结论:由式(1)、(2)可以看出，当带电粒子垂直射入有界匀强磁场的速率v一定(即粒子轨道半径一定)时，粒子的运动时间与弦长有关，圆心角θ在0～180°的范围内，弦越长、圆心角越大，带电粒子在磁场中做圆周运动的时间越长.

2 粒子速度大小方向均确定情况中弦的应用

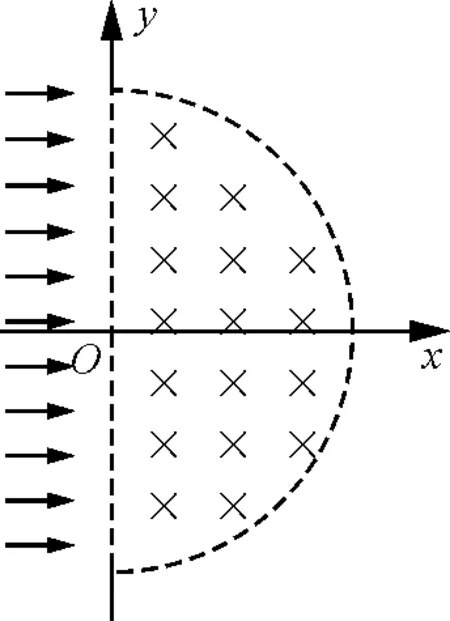
图2

【例1】如图2所示，在xOy平面内x>0处有一半圆形匀强磁场，磁场区域圆心为O，半径为R=0.10 m，磁感应强度大小为B=0.5 T，磁场方向垂直xOy平面向里.有一线状粒子源放在y轴左侧(图中未画出)，不断沿平行于x轴正方向放出电荷量为q=+1.6×10-19C,初速度为v0=1.6×106m/s的粒子，粒子的质量为m=1.0×10-26kg，不考虑粒子间的相互作用，粒子重力忽略不计，求粒子在该磁场中运动的最长时间，并指出该粒子入射时的坐标.

这是2011年某市高三理综调研卷中的一道试题，参考答案提供的解法如下.

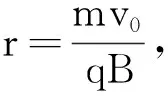
r=0.2 m

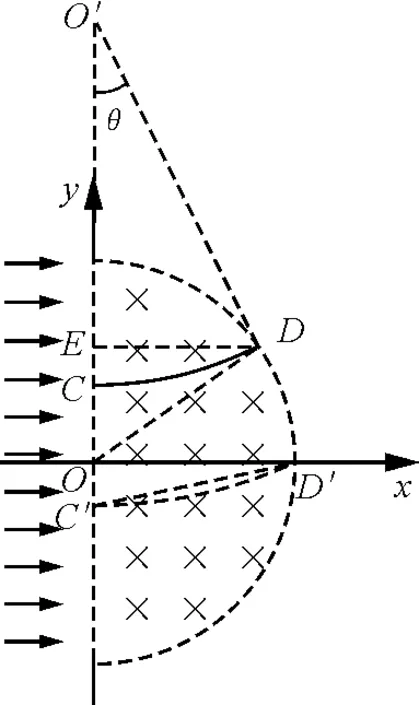
图3

在直角三角形ODE中，有

OE2+ED2=OD2

(3)

而OE=OO′-O′E=r+y-rcosθ

(4)

ED=rsinθ

(5)

将式(4)、(5)代入式(3)得

(r+y-rcosθ)2+(rsinθ)2=R2

化简得

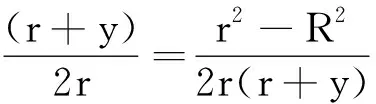
y=-0.027 m

此时

即入射点坐标为(0，-0.027)时，粒子的运动时间最长

代入数据得

tm≈6.5×10-8s

上述解答利用了求函数极值的方法，运算技巧要求高.其实利用轨迹圆对应的“弦”,可以很方便地确定哪一个粒子在磁场中运动的时间最长.

因为射入磁场的粒子速度相同，所以,它们在磁场中运动的半径均相同.要使得粒子在磁场中运动的时间最长即弦CD最长,圆心角θ最大，就要让ED最长.粒子的入射点变化时，其在磁场中的运动轨迹也将上下变动.当ED变到OD′时对应的弦C′D′最长，如图3所示.此时有

入射点C′的纵坐标y=-(r-rcosθm).代入数据可求得与前面相同的解.

3 粒子速度大小恒定 方向不确定情况中弦的应用

图4

解析:因射入磁场的粒子初速度大小相等，则它们的轨迹圆半径都相等.作动态变化轨迹圆，如图5所示.

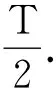
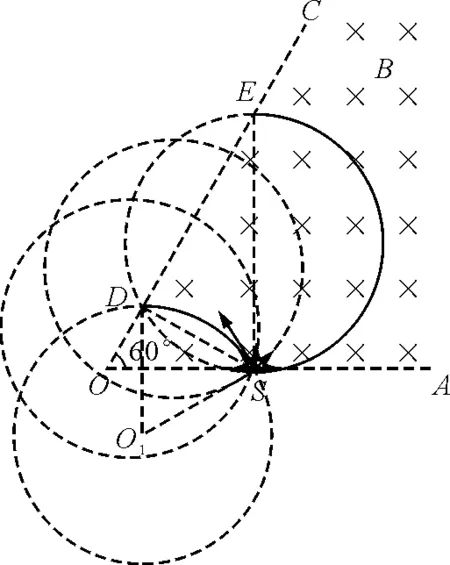
图5

(1)最后离开磁场的粒子从粒子源射出时的速度的大小；

(2)最后离开磁场的粒子从粒子源射出时的速度方向与y轴正方向夹角的正弦.

图6

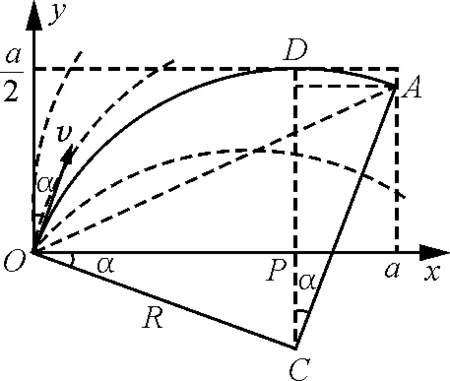
图7

(1)设粒子的发射速度为v，其做圆周运动的轨道半径为R，由洛伦兹力公式和牛顿第二定律，有

得

(2)设最后离开磁场的粒子的发射方向与y轴正方向的夹角为α，由几何关系得

Rsinα=a-Rcosα

且

sin2α+cos2α=1

解得

通过以上几例表明，利用圆中弦的性质，求解了带电粒子在磁场中的运动问题，只要教师加强引导，学生会有较好地理解和掌握.