旋转矢量法描述简谐波
麻志洪 陈亚琳 贾帆豪
(浙江师范大学数理与信息工程学院 浙江 金华 321004)
1 引言
旋转矢量法[1]是学习简谐振动过程中较为重要的解题方法,它将简谐振动的位移、相位、速度、加速度等变量在矢量图中表示出来.但笔者发现,利用旋转矢量法处理简谐波的文章并不多见,而学生在学习简谐波的过程中,对波的相位、时间性与空间性常感到困惑,故笔者将用旋转矢量法直观地描述简谐波.
2 方法分析
2.1 机械波旋转矢量法的引出(下文中均以波已传至所讨论的质点为例)
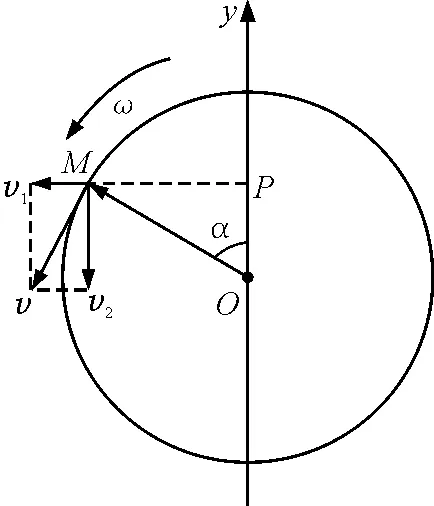
图1
如图1为旋转矢量图,矢端沿圆周运动的角速度为ω,设矢量与y轴的夹角为
α=ωt-kx+φ
(1)

y=Acos(ωt-kx+φ)
(2)
速度投影为
v=-Aωsin(ωt-kx+φ)
(3)
加速度投影为
a=-Aω2cos(ωt-kx+φ)
(4)
对于简谐波,设波动方程为
y=Acos(ωt-kx+φ)
(5)
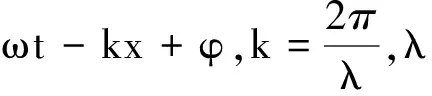
任意选定距波源右方x处的质点,则:
(1)旋转矢量以逆时针旋转为正,与y轴正向的夹角等于简谐波上位于距波源x处的质点在t时刻的相位,随着时间增长,相位增大,矢端逆时针转动;随着x增大,相位减小,矢端顺时针转动.
(2)旋转矢量的长度等于波的振幅,在y轴上的投影等于波上该质点的位移.
(3)矢端速度沿y轴方向的投影即是该质点的速度.
(4)矢端加速度在y轴上投影的负值即是该质点的加速度.
(5)该质点动能与势能的比值
对于第5点,由于位于x处的质点做类简谐振动,以弹簧振子为例做如下推导.
由动能公式知
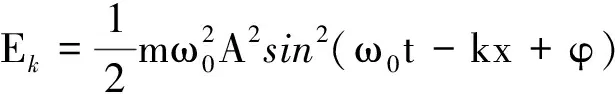
(6)
因为
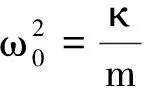
(7)
所以有
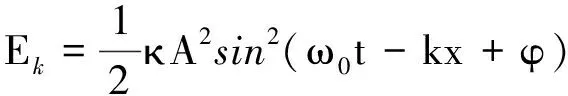
(8)
所以
(9)
势能
(10)
所以
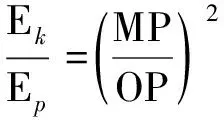
(11)
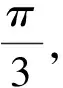
(1)距离波源右方12 m处的质点N在t=3 s时的相位;
(2)质点N在t=3 s时的振动方向以及动能与势能的比值.
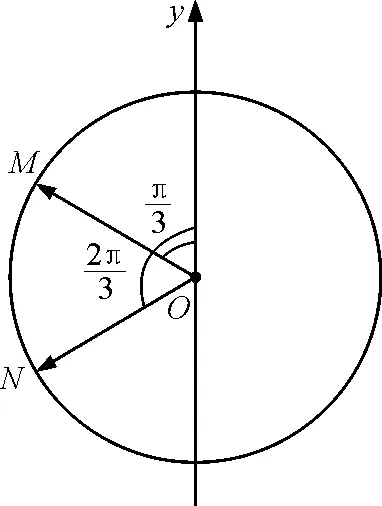
图2
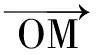
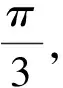
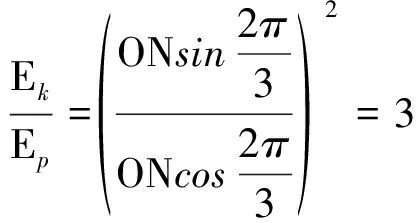
由此可见,利用旋转矢量法大大简化了问题.
2.2 同方向同频率简谐波的合成
同一介质中,两列同方向、同频率的简谐波可写成如下形式
y1=A1cos(ω0t-kx+φ1)
(12)
y2=A2cos(ω0t-kx+φ2)
(13)
则波的合成
y=y1+y2
(14)
式(12)、(13)代入式(14)整理,得
y= [A1cos(-kx+φ1)+
A2cos(-kx+φ2)]cosω0t-
[A1sin(-kx+φ1)+
A2sin(-kx+φ2)]sinω0t
(15)
令
Acos(-kx+φ)=
A1cos(-kx+φ1)+A2cos(-kx+φ2)
Asin(-kx+φ)=
A1sin(-kx+φ1)+A2sin(-kx+φ2)
则
y=Acos(ω0t-kx+φ)
(16)
可见,同方向、同频率的两列简谐波合成后仍为简谐波,其中
cos(-kx+φ)=
sin(-kx+φ)=

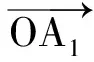
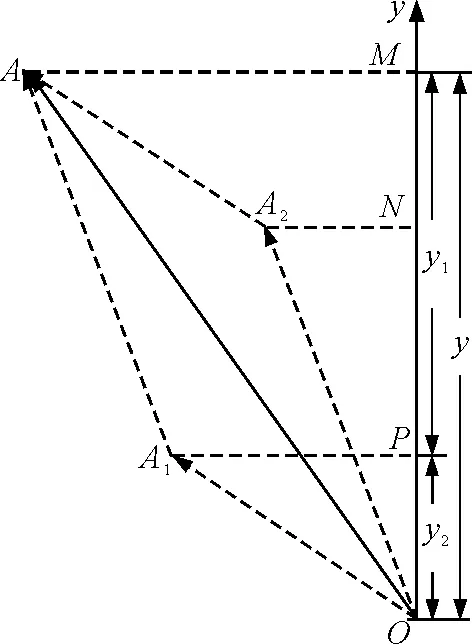
图3
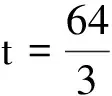
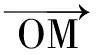
下振动,此时动能最大,势能为零.
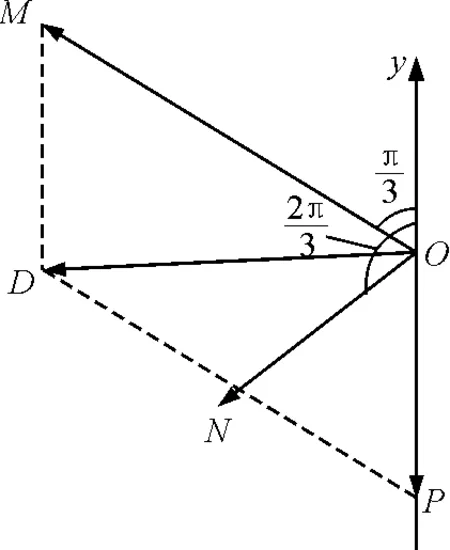
图4
该题若用代数法,因相位不同,非常繁琐,旋转矢量法则简单易行,该方法还可以解决波动方程的求解等问题,这里不再继续讨论.
3 结论
利用旋转矢量法描述简谐波,充分体现其时间和空间周期性,并通过矢量图将波上各质点的动能与势能比直观地反映出来,大大简化了有关波动问题的解决.
参考文献
1 赵凯华,罗蔚茵.力学.北京:高等教育出版社,2005
2 杨庆怡.用旋转矢量描述简谐振动.广西大学学报(自然科学版),2002(27)(Sup.):145~147
3 倪辛. 旋转矢量图与简谐振动的关系.南京广播电视大学学报,1999(4)
4 杨庆怡.用旋转矢量描述波形及振动曲线与波形的转换.见:第四届西部二十省(区)市物理学会联合学术交流会论文集.2008

