空间谱估计在Lamb波的结构损伤检测中的应用

张 宇， 郭 瑜， 薛 雷， 赵 磊

(1.西北工业大学 力学与土木建筑学院， 陕西 西安 710129；2.中铁第一勘察设计院集团有限公司， 陕西 西安 710043；3.中国建筑西北设计研究院有限公司， 陕西 西安 710016；4.贵州中建建筑科研设计院有限公司， 贵州 贵阳 550006)

空间谱估计是阵列信号处理中一种空域处理技术，由于其优越的空域参数(如波达方向)估计性能，从而在雷达、通信、智能天线、声纳等领域都得到了广泛的研究和应用[1]。从上世纪70年代起，在空间谱估计中涌现出的大量成果以Schmidt[2]等人提出的多重信号分类(MUSIC)算法最为突出，它具有测向精度高、分辨率高、能对多个来波信号同时测向及对瞬时短信号的测向等特点[3]。

利用Lamb波对结构进行损伤识别正成为一种经济有效的方法而逐渐得到广泛应用，现已成为结构健康监测领域的热点[4～6]。本文在利用Lamb波产生的阵列信号的基础上将多重信号分类(MUSIC)算法引入到结构损伤检测中。

1 MUSIC算法

MUSIC算法是利用接收数据的协方差矩阵分离出信号子空间和噪声子空间，利用信号方向向量与噪声子空间的正交性来构成空间扫描谱，实现信号的参数估计。

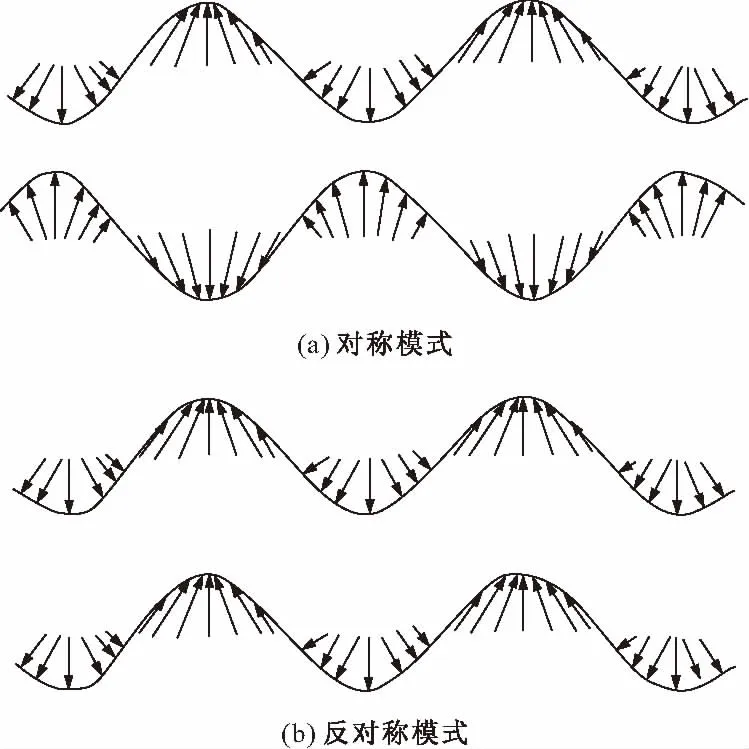
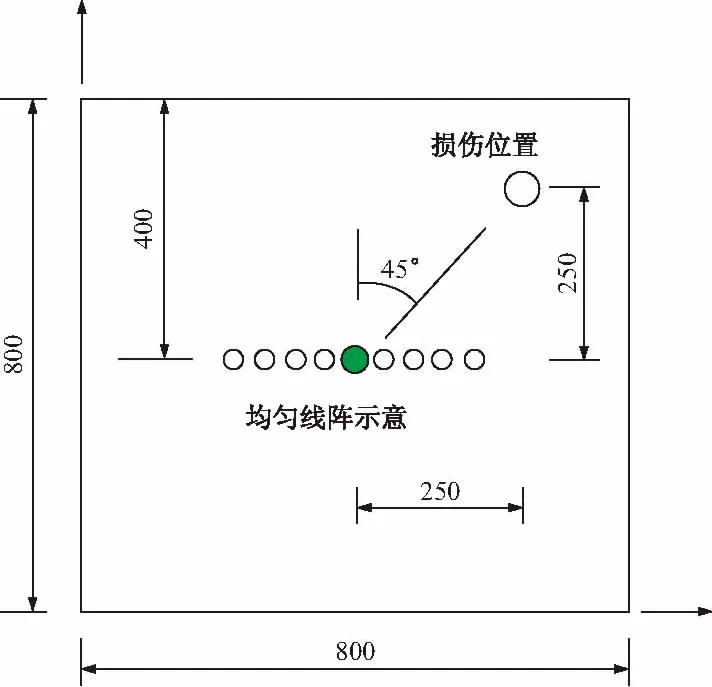
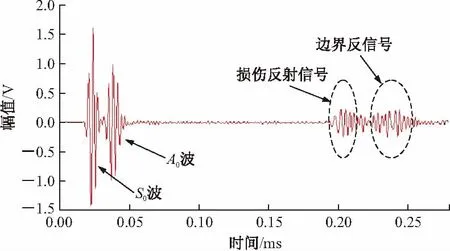
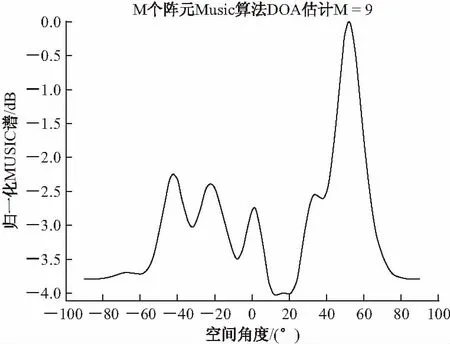
对于一个由M个阵元组成的已知任意几何形状基阵，假设有D(D

x(n)=A(ΘD)s(n)+n(n)

(1)

式中，A(ΘD)=[a(θ1),a(θ2), …,a(θD)]是M×D维阵列流形矩阵，s(n)=[s1(n),s2(n), …,sD(n)]T是D×1维信号源向量，n(n)是M×1维噪声向量。一般假设信号与噪声不相关。

数据协方差矩阵可以表示为

Rx=E{xxH}=A(ΘD)RsAH(ΘD)+Rn

(2)

式中，Rs与Rn分别为D×D维信号协方差矩阵与M×M维噪声协方差矩阵

Rs=E{ssH}

(3)

Rn=E{nnH}

(4)

对协方差矩阵Rx进行特征分解

Rx=EΛEH

(5)

式中，Λ是降序排列的特征值构成的对角阵，E=[Es,En]是对应的特征向量，Es与En分别是由较大的D个特征值与较小的M-D个特征值对应的特征向量组成的信号子空间和噪声子空间。

阵元域MUSIC方位谱函数为

(6)

式中，Θ表示观察扇面。

让θ在观察扇面内扫描，计算出式(6)在各扫描方位对应的函数值，该函数值出现峰值的方位即为信号方位估计值。在二维平面里，入射方向与阵列法向的夹角θ就是波达方向。本文中阵列为平面均匀线阵，如图1所示。

图1 均匀线阵

2 Lamb波基本原理

当波以某种角度入射极薄的复合材料或金属表面时，在适当的材料密度、弹性系数、厚度及波动频率下，会产生Lamb波，其作为一种典型的超声波，可以以对称模式和反对称模式在两个平行的平板表面进行传播。

在板厚为h的无限大固体自由板中，其频散方程为[8]：

(7)

(8)

(9)

其中，k为波在板中沿平行板表面方向传播的波矢，cL和cT为板材的纵波和横波传播速度，cp为波的相速度，ω为波的角频率。式(7)和式(8)分别为Lamb波对称模式的特征方程和反对称模式的特征方程，图2表示Lamb波的模式示意图。

图2 Lamb波的模式示意

工程中利用Lamb波对结构进行损伤检测已经被广泛应用。Yahiro[9]等利用Lamb传播的可视图像提出一种对复合材料结构的新无损检测技术。Lu[10]等利用Lamb波信号的建立传感器网络进行损伤识别。

可以看出，利用空间谱估计得到波达方向与Lamb波在损伤检测中的优点相结合能够为结构的损伤检测提供一种新的思路和方法。

3 仿真试验

选取一厚度为1 mm的铝板，尺寸为800 mm×800 mm。在绕x轴45°方向上开孔作为损伤假定，压电片作为激振器和传感器并且视为均匀线阵的阵元，其间距为在板上激励Lamb波长的一半，如图3所示。图中深色的压电片作为激励器，同时阵列中所有压电片作为传感器接收Lamb波信号。

图3 试验模型

选择汉宁窗修正的频率为300 kHz五周正弦信号为激励信号，得到的Lamb波传播过程中t=0.11 ms图形如图4所示。可以看出，S0波刚到达损伤位置，遇到结构损伤后，会有一部分被反射从而被线阵传感器接收，通过损伤反射信号估计其波达方向。

图4 Lamb波传播模型

图5为铝板中传播Lamb波的频散曲线图，可以看出，激励频率在300 kHz时，会产生S0和A0两种模式。

图5 Lamb波频散曲线

图6 阵列中一压电片响应信号

选取阵列中一个压电片，其采集波信号如图6所示。初始接收的直达S0波和A0波为激励后的直达波形，与频散曲线一致。信号中除了初始接收直达信号和由板边缘的反射波信号之外，中间的接收信号即为因结构损伤引起的反射波的响应信号。将阵列采集的Lamb信号代入式(6)，可以通过MUSIC算法得出损伤引起的反射波的波达方向。由图7可以看出，估计结果为48°，与假定并不完全一致。这是由于MUSIC算法对处理信号有一定的要求，同时，利用无限窄的激励信号激励Lamb波是物理不可实现的[11]。因此，只是使用MUSIC算法并不能完全达到损伤检测的要求。但是，如果对MUSIC算法进行改进，是可以提高检测精度的。这说明将空间谱估计方法引入到利用Lamb波进行结构损伤识别中是可行的。

图7 9个阵元时MUSIC算法对波达方向估计

4 结 语

本文提出了将空间谱估计中对波达方向的估计引入到结构损伤识别中，介绍了空间谱估计中最为突出及经典的多重信号分类算法(MUSIC)，并利用该算法对一损伤结构中的均匀线阵Lamb波信号进行分析，得到了比较满意的效果，这证明了空间谱估计在结构损伤识别应用中的可行性。然而，如果要得到满意的检测精度，则需要有改进的算法对波信号进行处理和分析。

[1] 甘 泉,孙学军,唐 斌. 一种基于空域滤波的空间谱估计方法[J]. 信号处理，2010, 26(2)：230-233.

[2] Schmidt R. Multiple emitter location and signal parameter estimation[J]. Antennas and Propagation, IEEE Transactions on, 1986, 34(3): 276-280.

[3] 王永良,陈 辉,彭应宁，等. 空间谱估计理论与算法[M]. 北京：清华大学出版社，2004.

[4] Su Z, Lin Y, Lu Y. Guided Lamb waves for identification of damage in composite structural: A review[J]. Journal of Sound and Vibration， 2006, 295(3):753-780.

[5] 袁慎芳. 结构健康监控[M]. 北京：国防工业出版社，2007.

[6] 朱宏平. 结构损伤检测的智能方法[M]. 北京：人民交通出版社，2009.

[7] 鄢社锋,马远良. 传感器阵列波束优化设计及应用[M]. 北京：科学出版社，2009.

[8] Rose Joseph L. 固体中的超声波[M]. 何存富, 吴 斌, 王秀彦译. 北京：科学出版社，2004.

[9] Yashiro S, Takatsubo J, Toyama N. An NDT technique for composite structures using visualized Lamb-wave propagation[J]. Composites Science and Technology, 2007, 67(15): 3202-3208.

[10]Lu Y, Ye L, Su Z. Crack identification in aluminium plates using Lamb wave signals of a PZT sensor network[J]. Smart Materials and Structures, 2006, 15(3): 839.

[11]苏永振,袁慎芳,王 瑜. 基于多重信号分类算法的复合材料冲击定位[J]. 复合材料学报，2010，27(3)：105-110.