基于云模型的地铁施工地表变形风险推理分析

吴贤国， 曹 靖， 张立茂,2， 宋若昕， 刘 倩

(1.华中科技大学 土木工程与力学学院， 湖北 武汉 430074；2. 马里兰大学 土木与环境工程学系， 美国 科利奇帕克 20742-3021)

城市地铁盾构施工时常引起地面沉降或塌陷，从而损坏道路路面、破坏地下已有管道以及建筑物和构筑物[1]，这些问题不仅严重影响人们生命财产安全和工程建设，并容易造成巨大的经济损失和社会影响，然而由于地铁施工环境的复杂性和影响因素的不确定性，在研究地铁施工引起的地表沉降问题时，传统的Peck公式、概率论、仿真分析、模糊集理论、解析法及可靠性分析理论受到较多的限制，造成实际工程中的大量数据难以直接用于实时施工风险预测，影响了地铁盾构施工诱发地表沉降的实时判断与预警控制[2]。

事故树分析法[3]是一种描述事故因果关系的逻辑“树”，它能对各种事件的危险性进行识别和评价，具有简明、形象化、系统性、准确性、预测性等特点。国际隧道协会《隧道工程管理指南》[4]中，事故树分析法被推荐用于风险管理工作。Huang[5]利用模糊事故树分析了轨道交通系统的可靠性，得出了以“火车相撞”为事故树顶事件的模糊概率。

本文将云模型方法引入事故树分析，在用事故树方法确定引起地表沉降过大因素的基础上，针对盾构隧道施工引起地表沉降影响因素众多，且具有模糊性和随机性，其影响因素难以量化、很难建立边界清晰的评判标准等特点，运用云模型方法处理专家对地铁盾构施工引发地表沉降过大的风险因素的定性评价，把自然语言中定性概念的模糊性和随机性有机结合起来，实现定性语言值和定量数值之间的转换，克服其影响因素难以量化的困难，使基本事件的评估概率更加客观、准确。基于工程实践建立盾构施工地表沉降事故树，在此基础上进行模糊事故树敏感性分析，得出盾构施工地表沉降风险的影响大的基本事件，从而有针对性地制定施工前地表沉降控制措施。

1 模糊事故树分析

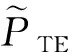
(1)

(2)

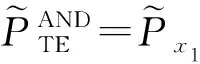
(3)

在之前的模糊事故树分析中，顶事件的概率仅仅给出了一个关于系统的概念，不顾每个基本事件的贡献程度。确定不同基本事件的重要等级是决策分析的本质，因此敏感性分析运用于识别系统最弱组成部分(Contini et al., 2000)[8]。

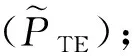
(4)

2 基于云模型的模糊推理机制

在模糊概率分析中,由于缺乏足够的数据，对失效概率很难有一个准确的估计。以云模型来替代隶属函数可以弥补常规模糊评价模型的不足，将专家的评价转换成云图，通过对云图的鉴别可以加强专家对基本事件的理解，从而解决信息分散、主观臆断的偏差。

2.1 云模型及其模糊化运算

云是用语言值描述的某个定性概念与其数值表示之间的不确定性转换模型，即云模型是定性定量间转换的不确定性模型[10]。它主要反映知识概念中的两种不确定性：模糊性和随机性。设U是一个论域U={x}，T是与U相联系的语言值。每一个x称为一个云滴。μ(x) 在[0,1]中取值，云是从论域U到区间[0,1]的映射，即μ:U→[0,1 ],x∈U,x→μ(x) 。

云的数字特征[11]用期望值(Ex)、熵(En)、超熵(He)三个数值来表征,它们反映了定性知识的定量特性。其中期望值Ex是概念在论域中的中心值，是概念量化的最典型样本；熵En是定性概念模糊度的度量，反映了在论域中可被这个概念所接受的数值范围，即离散程度越大，概念所接受的数值范围也越大，概念越模糊。超熵He可谓En的熵，反映了云滴的离散程度。超熵越大，云滴离散度越大，隶属度的随机性越大，云的“厚度”也越大。

云模型的3个数字特征值把模糊性(定性概念的亦此亦彼性)和随机性(隶属度的随机性)完全集成到一起，构成定性和定量相互间的映射，作为知识表示的基础[12]。

2.2 基于云模型的模糊化设计

(1)基于专家群决策得到基本事件风险概率大小定性描述对应的定量描述

事故树分析时，首先要对基本事件风险概率大小进行分布范围划分，基于专家群决策确定基本事件风险概率分布范围划分时，由于地铁工程的复杂性，导致不同的专家对于地铁盾构地表沉降风险概率评价不一，倾向于得到不同的判断。因此非常有必要用云模型转换专家的不同定性语言，形成可用于计算并且满意的定量数值。基于专家群决策确定基本事件风险概率分布范围划分时，对于地铁盾构地表沉降风险的大小，首先进行定性描述，一般采用五级标度法，即V={V1,V2,V3,V4,V5}={较大,中等,小,偏小,很小}，对应的定量值取值范围在[0,1]区间。由于自然语言评语具有模糊性，因此可以采用正态云来描述每个评语。邀请n位专家对基本事件的概率进行评价，即对较大,中等,小,偏小,很小的风险概率进行定量评价，得到基本事件发生概率较大,中等,小,偏小,很小的定量描述xi。

(2)通过逆向云发生器获取特征数字

接下来，运用公式(5)来简化、合成和计算地铁盾构施工地表沉降风险概率的三个特征参数，即Ex,En,He。

(5)

(3)根据云模型数字特征借助正向云发生器生成云图

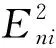
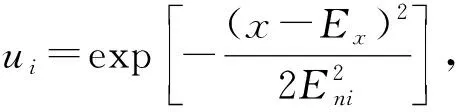
d.重复a到c，直到产生要求的n个云滴。

(4) 根据风险云图凝聚性，运用上述方法获取基本事件概率大小的定量表达

借助正向云发生器生成云图，判断专家对风险值大小的离散程度。其中，期望表示专家评价的平均水平；熵表示评价的离散程度，体现专家的水平；超熵表示与正常发挥时的偏离程度，综合反映专家的心理素质和思考状态等因素。

如果云图凝聚性差，则重复上述步骤，直到专家意见较为一致，即可确定风险因素发生概率各语言描述值的定量表达参数Ex、En、He。

(5) 基于专家定性评价和信心指数修正获得基本事件概率

采用专家调查法获得专家对各基本事件发生概率大小的定性描述，基于前面云模型确定的风险较大,中等,小,偏小,很小对应的各基本事件发生概率大小的定量描述，同时在专家调查法中，引入信心指数θ进一步修正专家调查法中得到的数据，θ从高～低依次为 10～1，表示专家对评价结果的确定程度，引入信心指数可提高结果的精确性。基于信心指数修正获得各专家评价的基本事件风险较大、中等、小、偏小、很小对应的概率大小的三角模糊数定量描述采用公式(6)计算，当存在多个专家评价时，取平均值计算。

(6)

3 案例研究

3.1 地铁盾构施工地表沉降事故树的建立

盾构隧道施工引起地表沉降的因素很多，根据工程项目基本理论和地铁施工安全特性，从“人—机—材料—环—管理”的角度分析地铁施工中可能存在的危险源，归纳得到盾构隧道工程地表沉降存在的主要风险因素。根据对盾构隧道工程地表沉降致险因子的辨识结果，本文构建了盾构隧道工程地表沉降事故树，如图1所示。图中各符号所代表的事件见表1。

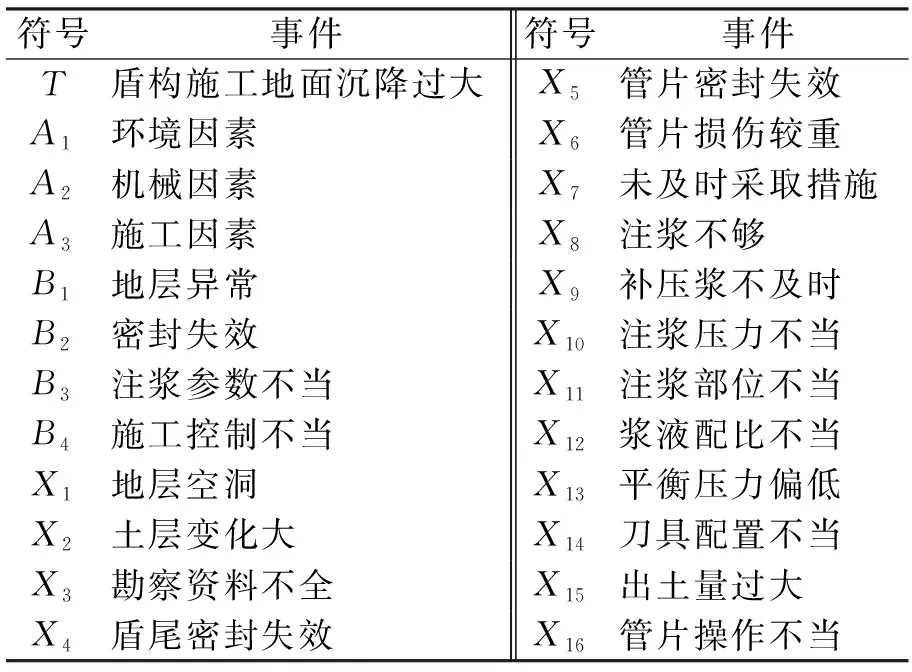
表1 地铁盾构施工地表沉降基本事件

图1 地铁盾构施工地表沉降事故树

3.2 模糊概率获取

(1)风险概率分析评价

邀请10位专家，各位专家基于对地铁盾构施工地表沉降的知识储备、风险度量和相关经验，对地铁盾构地表沉降风险基本事件概率分布进行评价，给出对较大,中等,小,偏小,很小的风险概率分布范围的定量评价值xi，如表2。

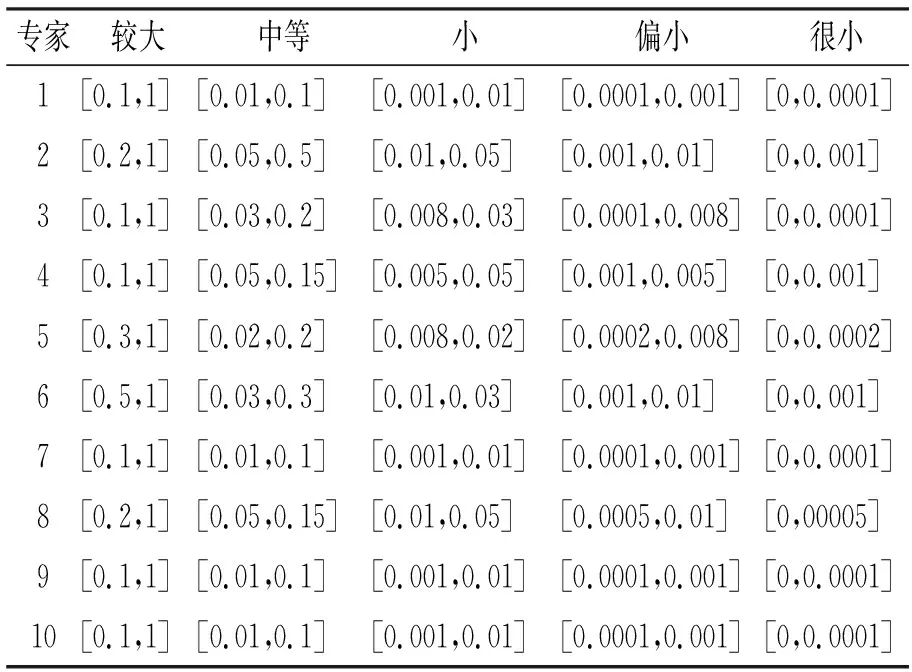
表2 专家评价5级风险的概率分布

(2)通过逆向云发生器获取云模型特征数字

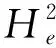
(3)根据云模型数字特征借助正向云发生器生成云图

借助正向云发生器，输入反映定性概念的数字特征(Ex,En,He)及云滴数n，产生云图。

根据公式(5)可以计算出每个基本事件对应的云特征数字，以定性语言“较大”为例，根据计算出的云特征数字，生成云图如图2所示。

由图2(a)可知专家在第一轮对“较大”概念的理解有待加强，信息比较分散，熵和超熵都较大，每个数值隶属于相应语言值的隶属度的随机性变化也较大。将第一轮专家评价的结果经过筛选分类和归纳整理反馈给专家进行第二轮专家评价时，专家根据大部分专家的意见，调整自己的评价结果，得到评价结果的云数字特征为(0.58,0.1260,0.036)，熵和超熵逐渐减小，云图2(b)所示。将第二轮专家评价的结果整理后再次反馈给专家，进行第三轮专家评价得到数字特征为(0.55,0.1230,0.012)，熵和超熵值再次减小，得到的云图凝聚性再次增强，表示专家意见统一，如图2(c)所示，因此获得定性语言“较大”的概率范围为[0.15,1]。

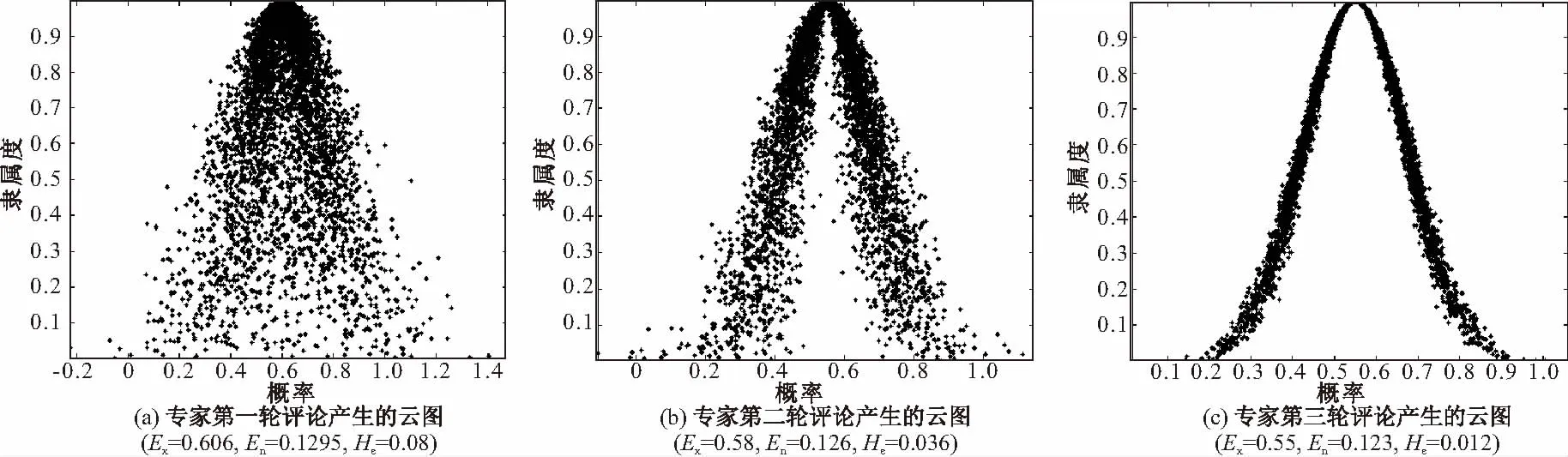
图2 定性语言“较大”专家评价的云图变化

(4)根据风险云图凝聚性，得到风险的分布范围

运用上述方法可以计算出不同风险等级每轮评价的数字特征，如表3所示。由表3可计算出风险因素概率值分布范围，如表4所示。

表3 不同风险等级3轮评价的数字特征

表4 风险因素概率分布范围

(5)基于专家定性评价和信心指数修正获得基本事件概率

根据步骤(4)计算出的概率值分布范围，采用专家评价法对各基本事件给出发生概率为较大～很小的定性语言评价和信心指数(表5)，运用公式(6)计算得到基本事件概率三角模糊数，结果见表6。

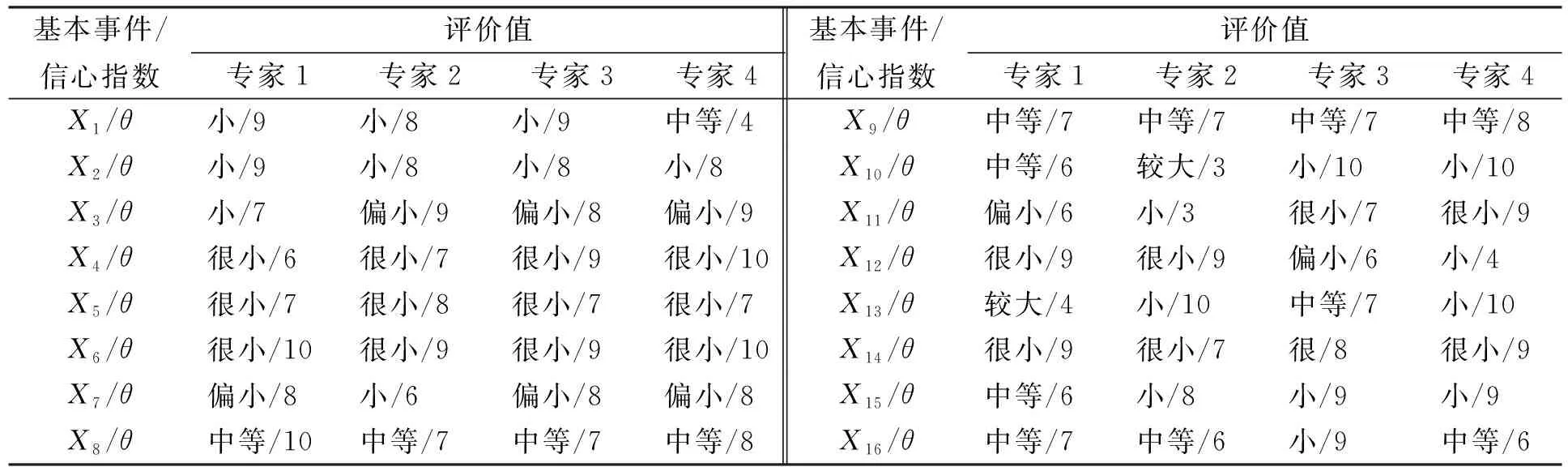
表5 专家对基本事件概率大小和信心指数评价

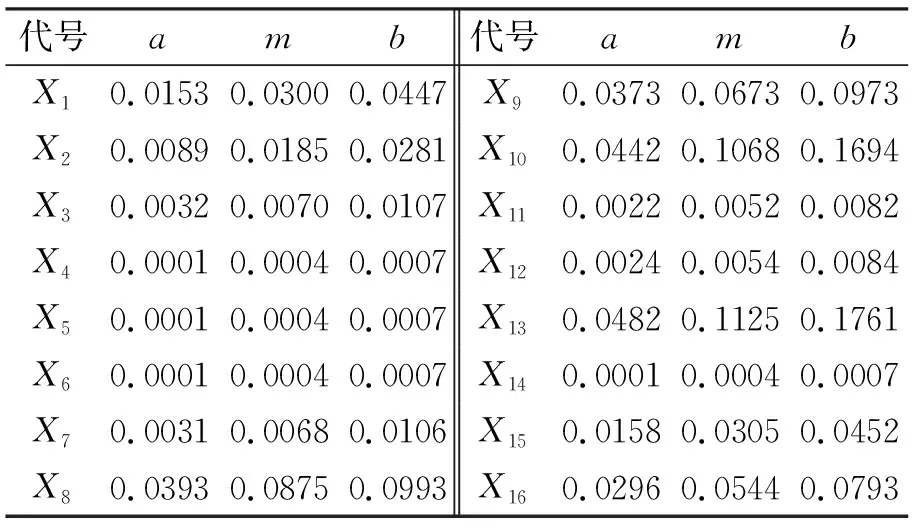
表6 基本事件三角模糊概率

(6)顶事件概率计算

根据公式(2)、(3)，按事故树结构从下至上逐层计算。中间事件概率及顶事件模糊概率如表7所示。

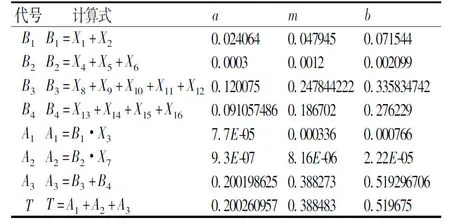
表7 中间事件及顶事件三角模糊概率

根据计算得出顶事件T的模糊概率可能性分布为<0.200，0.388，0.520>。该模糊概率可能性分布标明：盾构隧道工程施工渗漏水事故最可能发生概率为0.388，波动范围是(20%，52%)。

3.3 模糊重要度分析

(1)由表8可以看出，基本事件模糊重要度排序为:X13>X10>X8>X9>X16>X15>X12>X11>X14>X3>X1>X2>X4=X5=X6=X7，计算结果与传统事故树方法是一致的。X13(平衡压力偏低)、X10(注浆压力不当)、X8(注浆不够)对地铁盾构施工地表沉降的发生影响最大，这与地铁施工实际风险控制也相吻合，因此基于云模型的模糊事故树是相当可靠和有效的。

(2)基于云模型的模糊事故树充分考虑了群体资深专家的主观偏差、地铁施工随机性和偶然性，利用云图的凝聚性将误差最小化。从上述计算结果可以看出，基本事件2(土层变化大)和基本事件3(勘察资料不全)的模糊重要度非常小，并且十分接近，因此基于云模型的事故树分析方法提供了更为精确的基本事件概率，从而对地铁盾构地表沉降提供了精确的预警。

(3)基于云模型的模糊事故树分析方法，将工程领域多源数据中随机与模糊不确定性因素结合起来并同时考虑，克服了概率论与模糊集理论方法仍然存在的局限，分析结果为风险控制和预防提供了建设性意见。

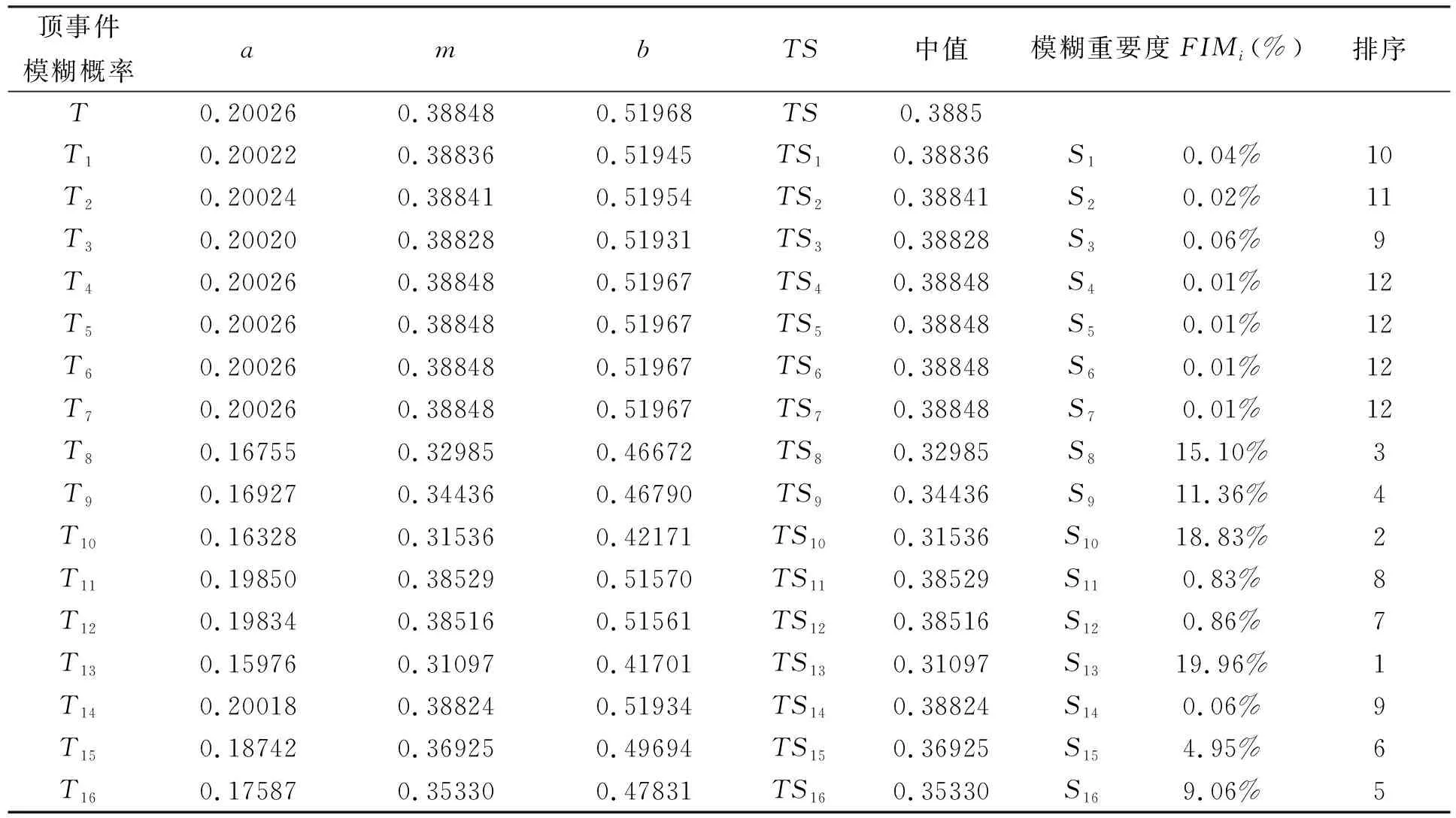
表8 模糊重要度分析

4 结 论

(1)本文提出了基于模糊事故树和云模型结合的地铁盾构施工地表沉降分析方法，评估过程规范、简单，克服了转换专家存在主观因素和不确定性自然语言的困难。在充分考虑地铁资深专家给出的评价范围内，通过云模型在一定程度上修正了风险发生概率的分布范围，将实际数据与经验数据结合起来，准确、客观的得到影响地铁盾构地表沉降基本事件的概率，使得分析结果更合理，贴近工程。

(2)专家信心指数修正法被证明可以进一步精确云模型计算结果。本文引入信心指数修正各专家评价的基本事件风险较大、中等、小、偏小、很小对应的概率大小的三角模糊数定量描述，结果更为精确。

(3)基于云模型的地表沉降模糊故障树定量分析，得出基本事件X8(注浆不够)、X10(注浆压力不当)、X13(平衡压力偏低)对顶事件的发生影响最大的结论，并且该结论同工程实际相吻合，具有工程实用性。因此，在地铁盾构施工过程中，应当重点防范注浆不够、注浆压力不当和平衡压力偏低等因素对地表沉降的作用，采取控制措施将风险减到最小。

[1] Valizadeh Kivi A, Sadaghiani M H, Ahmadi M M. Numerical modeling of ground settlement control of large span underground metro station in Tehran Metro using Central Beam Column (CBC) structure[J]. Tunnelling and Underground Space Technology, 2012, 28: 1-9.

[2] Wang Z, Wong R C K, Li S, et al. Finite element analysis of long-term surface settlement above a shallow tunnel in soft ground[J]. Tunnelling and Underground Space Technology, 2012, 30: 85-92.

[3] 郑俊杰，赵冬安，林池峰. 三角模糊数故障树法在盾构隧道成本分析中的应用[J]. 土木工程与管理学报, 2012，29 (4):1-5.

[4] Degn Eskesen S, Tengborg P, Kampmann J, et al. Guidelines for tunnelling risk management: international tunnelling association, working group No. 2[J]. Tunnelling and Underground Space Technology, 2004, 19(3): 217-237.

[5] Huang H Z, Xu Y, Xin S Y. Fuzzy Fault Tree Analysis of Railway Traffic Safety[C]// Traffic and Transportation Studies, Beijing: American Society of Civil Engineers, 2000 : 107-112.

[6] 杨军等. 装备智能故障诊断技术[M].北京: 国防工业出版社, 2004.

[7] Abbasbandy S, Hajjari T. A new approach for ranking of trapezoidal fuzzy numbers[J]. Computers & Mathematics with Applications, 2009, 57(3): 413-419.

[8] Contini S, Scheer S, Wilikens M. Sensitivity Analysis for System Design Improvement[C]//Dependable Systems and Networks, 2000. DSN 2000. Proceedings International Conference on. IEEE, 2000: 243-248.

[9] Ferdous R, Khan F, Veitch B, et al. Methodology for computer aided fuzzy fault tree analysis[J]. Process Safety and Environmental Protection, 2009, 87(4): 217-226.

[10]李德毅. 知识表示中的不确定性[J]. 中国工程科学, 2000, 2 (10) : 73-79.

[11]Wang H, He S, Liu X, et al. Simulating urban expansion using a cloud-based cellular automata model: A case study of Jiangxia, Wuhan, China [J]. Landscape and Urban Planning, 2013, 110: 99-112

[12]Li L, Liu L, Yang C, et al. The comprehensive evaluation of smart distribution grid based on cloud model[J]. Energy Procedia, 2012, 17: 96-102.

[13]余宏亮，丁烈云，余明晖. 地铁工程施工安全风险识别规则[J]. 土木工程与管理学报，2011, 28 (2): 77-81.