基于最优强度的SUV车架轻量化设计

敬扬名

(泸天化弘旭工程建设公司，四川 泸州 646300)

传统的车架结构设计由于采用经验及类比法，车架质量过重且应力分布不均匀［1］。因此，有必要对车架进行结构优化以提高车架材料的使用率。本文以某型SUV车架为研究对象，以应力强度为约束条件，利用APDL语言对车身结构参数化建模进行了结构优化设计。

1 优化设计数学模型的建立

优化问题的数学模型是实际优化设计问题的数学抽象，建立近似车架优化设计数学模型有的数学途径有一阶 Taylor展式等［2］。

以结构重量为目标函数，包含车架应力强度约束的优化问题可以描述为:

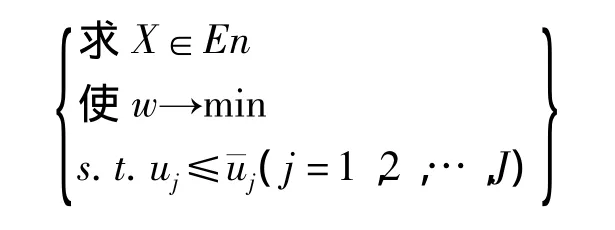
2 车架模型原设计技术参数

表1 车架各项技术参数

该型SUV车架由2根纵梁，5根横梁，1根扭杆梁，1根变速箱梁和前后副杠组成，其技术参数如表1所示。该车架材料为16 Mn钢，机械性能为:最小屈服强度 360 MPa;最大抗拉强度 610 MPa［3］。

由于车架结构的体积与重量成正比，因此车架轻量化问题可以转化为求解车架体积最小化问题。整个车架体积是通过各梁的截面积及各梁长度确定，由于安装的需要，车架各梁的拓扑结构不能改变，因此，只能通过对各梁的截面积优化来达到减轻车架重量的目的。

3 车架各梁截面参数化表示及优化部分程序

借助ANSYS软件进行优化设计，需先对车架进行参数化建模［4］。车架梁的最大厚度为4 mm(车架第1纵梁)，厚度最小为2.5 mm(为第7梁)，其他梁的厚度为3 mm。因此，本文仅对车架横、纵截面的长、宽进行优化。各截面的参数化表示见图1。图1中B、H为纵梁截面的长和宽;R1、R2、R3为第1横梁、第5横梁、第 6 横梁截面半径;B1、H1、B2、H2、B3、H3、B4、H4为 2 横梁、变速箱梁、扭杆梁、第 7 横梁截面的长和宽。

生成循环所用的分析文件并求解，提取并指定状态变量和目标函数。然后进入OPT处理器指定分析文件及优化变量、指定优化循环控制方式后进行优化分析。部分程序［5］为:

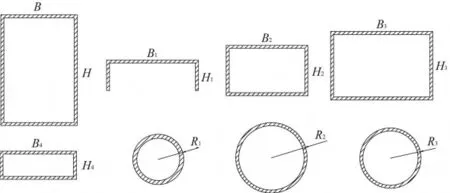
图1 各梁截面的参数化表示

4 车架优化的结果

车架优化的结果如图2～5所示，限于篇幅，不再列出B4与H4、R1、R2、R3的变化曲线。

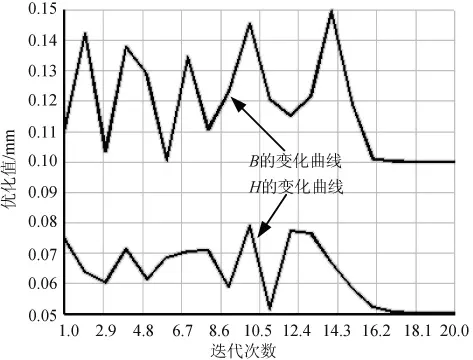
图2 B与H的变化曲线

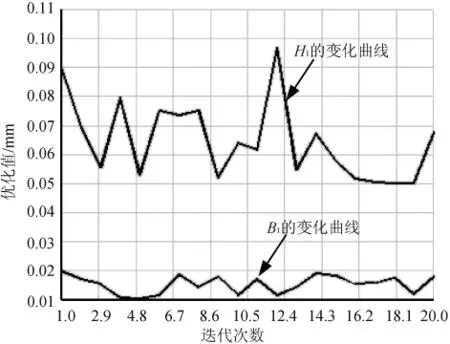
图3 B1与H1的变化曲线

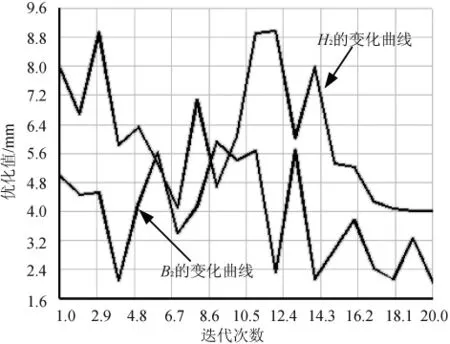
图4 B2与H2的变化曲线

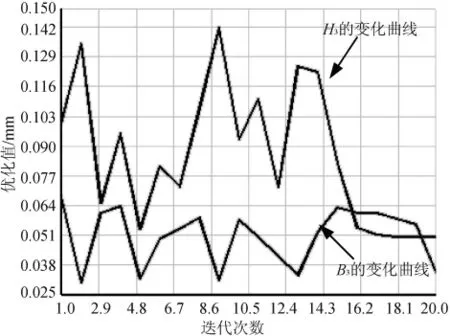
图5 B3与H3的变化曲线

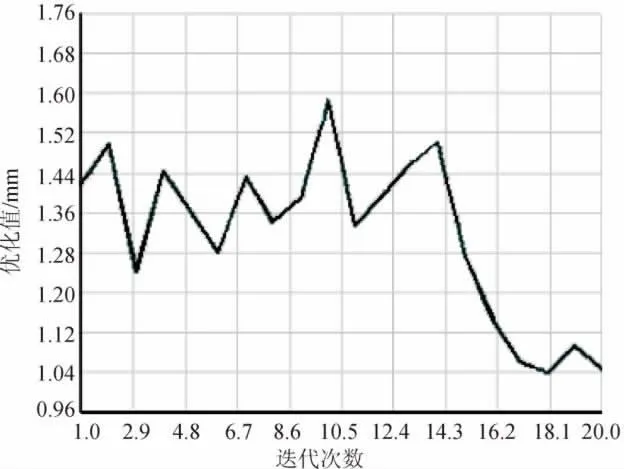
图6 体积收敛曲线

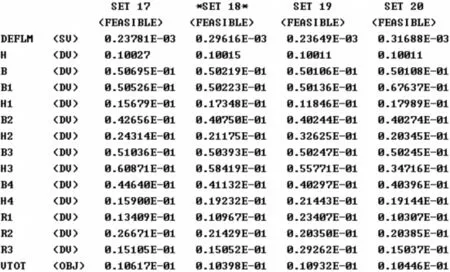
图7 ANSYS计算后各步参数列表

图6为目标函数即车架总体积随计算迭代次数的变化曲线，可以看出车架的总体积在1～13步之间大幅振荡，随着迭代次数的增加在第14步后开始收敛，到第18步达到最优值。图7为软件计算后给出的各步参数的最优值，其中*号为程序选择的最优步。优化后车架的体积为10.932 dm3，车架的最大变形量为236.49 m。

将车架结构初始设计与结构优化后结果对比，结果如表2所示。

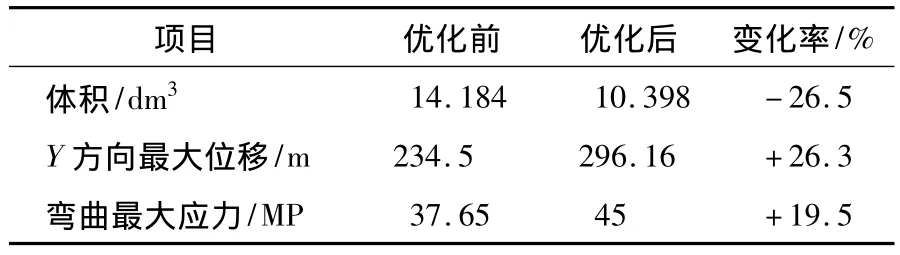
表2 优化结果对比

从表2可知优化结果很明显，车架的总体积减少了26.5%，采用同一材料，则重量减轻了26.5%;Y方向的最大位移增加了26.3% ，弯曲时最大应力增加了19.5%。位移和弯曲应力有所增加但仍在车架材料及车架使用要求范围内。

5 结语

本文对该SUV型车架进行了参数化建模，利用ANSYS13.0软件中的APDL语言编写了车架的优化程序，以车架各梁的截面尺寸为设计变量，以车架的应力为约束条件，以车架的体积为目标函数对车架进行了优化分析。车架重量减轻了26.5%，其优化效果非常明显。通过将该优化后的车架生产试验，结果表明其最大应力与计算相符，完全能满足车辆开发的验证试验。

［1］孙蕾，任晓琳，孟辉.基于ANSYS的桥梁结构拓扑优化设计［J］.中国高新技术企业，2009(20):38－39.

［2］ZHOU M.Difficulties in truss topology optimization with stress and local bucking constraints［J］.Structural Optimization，2006(11):134 －136.

［3］温秉权.金属材料手册［M］.北京:电子工业出版社，2009:103－105.

［4］王志明.太阳能电动三轮车车架结构性能仿真份析及优化研究［D］.杭州:浙江大学，2006:63－65.

［5］龚曙光，谢桂兰.ANSYS操作命令与参数化编程［M］.北京:机械工业出版社，2004:77－93.