关于矩阵Jordan标准形研究性教学的探讨

赵琳琳

（德州学院 数学系，山东 德州 253023）

矩阵的Jordan标准形是线性代数的中心结果之一，不仅在矩阵理论与计算中起着十分重要的作用，而且在控制理论、系统分析、力学等领域中也是一个非常重要的工具.由于Jordan标准形涉及到相似、Jordan块，计算又用到初等因子，这使得大多学生感到晦涩难懂不易理解.在当今大学提倡研究型教学的形势下，教师在讲授Jordan标准形的同时，让学生接触一些它的性质和应用，可加深学生对Jordan标准形这一经典理论的理解，为后继研究学习奠定基础.结合教学与科研工作体会，本文从为什么研究矩阵特征Jordan标准形、怎么研究及其应用等方面给出了矩阵Jordan标准形研究性教学的几点体会.

1 为什么研究矩阵Jordan标准形

我们知道，相似矩阵有相同的迹、行列式、特征多项式和特征值，但反之不一定成立.另外，两个看上去很不相同的矩阵仍可以相似，从而引出这样一个问题：在什么情况下两个矩阵相似？一个比较自然的想法是：设想有某个具有指定形式的“简单”矩阵的集合，然后看这两个已知矩阵是否可以通过相似化成这些“简单”形式中的一个.如果可以，它们就相似，因为相似关系具有传递和对称性.那么什么样的“简单”形式能符合这个要求呢？最容易想到的就是对角矩阵，但它不一定总能实现；其次是上三角矩阵，但是上三角矩阵有m(n+1)/2个元素需考察，数目太大.如果对每一个矩阵来求一个尽可能接近对角矩阵的上三角形式，而且还可以用相似变换得到，问题就解决了，所得结果就是Jordan标准形.在一般的教材中，大多是直接给出Jordan标准形的结论，很少介绍为什么要研究Jordan标准形.若在教学中加入这些细节，可以使学生知其然也知其所以然，也能使学生较容易接受，对培养学生的独立思考能力和学习兴趣有很好的作用?.

2 怎么研究矩阵Jordan标准形

Jordan标准形定理的内容是：每一个复方阵A都相似于一个Jordan矩阵

是一个ni阶的Jordan块，n1+n2+…+nk=n.Jordan矩阵J称为矩阵A的Jordan标准形，它在不计对角Jordan块的顺序时是唯一的.

由于标准形定理涉及到Jordan块及Jordan矩阵，教学中我们可以从Jordan块的性质、Jordan矩阵的结构以及标准形的计算等方面来学习矩阵的Jordan标准形.

2.1 Jordan矩阵的结构性质

Jordan矩阵J是一个“近乎对角”的有确定结构的矩阵，由这一结构可以较容易看出该矩阵以及与其相似的任意矩阵的某些性质，列举如下[2,3]：

（1）Jordan块的个数k是J的线性无关特征向量的个数，J可对角化当且仅当k=n.

（2）对 ni阶的 Jordan块 Jni(λi)，有

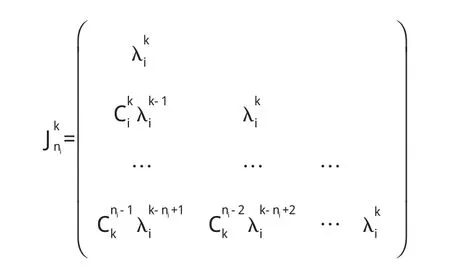
且(Jni-λiI)k=0圳k≥ni.

（3）Jordan矩阵给出了矩阵A特征子空间的精细结构，即相应于一个已知特征值的Jordan块的个数是相应的特征空间的维数.

（4）Jordan矩阵J的所有子块 Jni(λi),i=1,2,…,k的阶数可以通过分析某些幂的秩来确定.如果λ1是n阶矩阵J的特征值，则取幂(J-λ1I),(J-λ1I)2,…,最终(J-λ1I)k的秩将停止下降，使(J-λ1I)k的秩达到它的极小值的那个最小的k值就是相应于λ1的最大子块的阶.例如：如果

经计算得，rank(J-2I)=5，rank(J-2I)2=3，rank(J-2I)3=2,rank(J-2I)4=2.这组数足以确定相应于λ1=2的Jordan子块的分块结构.由rank(J-2I)3=rank(J-2I)4=2，可得相应于λ1的最大子块的阶是3，rank(J-2I)2-rank(J-2I)3=1是3阶子块的个数，因而只有一个3阶子块，rank(J-2I)-rank(J-2I)3=3是3阶子块个数的2倍加上2阶子块的个数，因而有一个2阶子块，一阶子块的个数等于 8-rank(J-2I)3-3×1-2×1=1.对 λ2，λ3，等等可作同样的分析，因而可确定出所有的子块.

在教学过程中，让学生适当地了解上述一些有关Jordan矩阵的性质，有助与加深他们对Jordan矩阵这一概念的理解，为下面的Jordan标准形的学习和计算提供感性的认识和必要的基础.

2.2 Jordan标准形的计算

Jordan标准形是线性代数的经典结论之一，从而有必要让学生了解Jordan标准形的一些求解方法.对于给定的 阶矩阵A，怎样求A的Jordan标准形？教材[1]利用的是矩阵的初等因子.例如：给定矩阵

经计算得A的初等因子是λ-1，(λ-1)2，那么A的Jordan标准形是

除此之外，根据Jordan矩阵的性质（4），还可以通过以下步骤来确定：

第一步，求出它的所有不同特征值；

第二步，对 A的每个不同的特征值 λi，作(A-λiI)k，其中k=1,2,…,n，然后分析这些矩阵的秩所组成的序列，得到相应于λi的所有Jordan块的阶数与个数.

解 经计算得矩阵A的特征值为1，且

从而rank(A-I)=1.由(A-I)2=0说明相应于1的最大子块的阶是2，(A-I)的秩就是2阶子块的个数，因而只有一个2阶子块.因此可得A的Jordan标准形是

2.3 Jordan标准形的组合刻画

由Jordan标准形定理可得：两个矩阵相似当且仅当它们有一个共同的Jordan标准形.用S(A)表示与A相似的所有矩阵的集合，符号覬(A)表示矩阵A的非对角位置的非零元的个数.如果不计较置换相似，矩阵的Jordan标准形J(A)是S(A)中非对角位置零元素的个数达到最大的唯一的形式[4]，这就是Jordan标准形的组合刻画.

3 矩阵Jordan标准形的应用

有了矩阵的Jordan标准形，我们可以很容易地了解矩阵是否可逆，是否可对角化，也能较轻松地得到它的行列式因子、初等因子等.除此外，Jordan标准形在线性微分方程组的求解以及矩阵分解中应用广泛，参见文献[2]和[3]，然而在教材中很少涉及，作为教师的我们可适当地加进一些Jordan标准形的如下几点应用：

3.1 利用Jordan标准形证明Hamilton-Cayley定理

Hamilton-Cayley定理 设A为n阶复矩阵，f(λ)是A的特征多项式，则f(A)=0.

证明[3]设A的特征值为λ1,λ2,…,λn且存在可逆矩阵P，使得PAP-1=J，这里J为A的Jordan标准形，可得

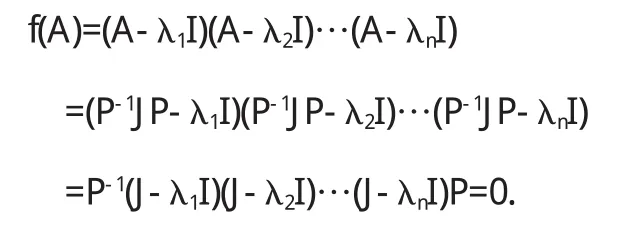
3.2 Jordan标准形在矩阵分解中的应用

命题1[5]复数域上任何n阶方阵，都可以写成两个对称矩阵的乘积.

命题2[5]设A为n阶复矩阵，那么A可写一可对角化矩阵与一幂零矩阵的和.

3.3 Jordan标准形在线性微分方程组求解中的应用

例[2]解下列微分方程组

解 首先把微分方程组改写成矩阵形式：

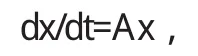
然后对微分方程组施行一个非奇异线性变换，即：x=Py，其中

于是，就有

从而其一般解分别为

再由x=Py，得原微分方程的一般解为

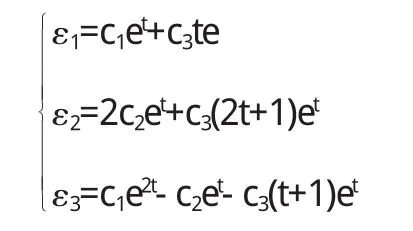
由此可见，Jordan标准形在求解某些线性微分方程组时，可以较大的简化求解步骤，这样就在一定程度上扩大了线性微分方程组的应用领域，反过来也促使人们致力于矩阵Jordan标准形的研究与发展.

〔1〕北京大学数学系几何与代数教研室代数小组.高等代数（第二版）[M].北京：高等教育出版社2011.

〔2〕R.A.Horn,C.R.Johnson.Matrixanalysis[M].CambridgeUniversityPress,1985.

〔3〕李桂荣,孙杰,刘耀斌.Jordan标准形矩阵的性质及应用[J].德州学院学报,2003,19（4）：20-24.

〔4〕詹兴致.矩阵论[M].北京：高等教育出版社,2008.

〔5〕张贤达.矩阵分析与应用[M].北京：清华大学出版社，2004.