辅助函数在高职数学教学中的应用

何润民

(陕西工业职业技术学院，陕西咸阳 712000)

辅助函数在高职数学教学中的应用

何润民

(陕西工业职业技术学院，陕西咸阳 712000)

在高职数学教学中，构造辅助函数是常见的思想方法。对构造辅助函数的研究，对于开阔学生的思路，培养他们的创新意识和分析问题、解决问题的能力具有十分重要的意义。

构造法;辅助函数;思想方法

辅助函数是构造法的产物。简单说：就是为了使某一数学命题或某一数学概念通过已知的数学概念和方法人为地构造出来的函数，这些函数的存在往往依赖于已知函数的存在，在较强的条件约束下，达到证实或说明某种结论或概念的正确性。辅助函数在高等数学中广泛地被采用着，它们起桥梁的作用，有些甚至无法替代，辅助函数在数学发展过程中的独到作用是不容忽视的。

针对高职数学教学过程中，一些定理和结论的证明当使用通常方法很难奏效时，往往需要先构造一个与所证结果有关的辅助函数，作为解决问题的桥梁，然后运用已知条件和有关概念，推证出所要证的结果，这就是构造辅助函数的思想。

一、借助几何直观构造辅助函数

利用数形结合的方法，借助与几何图形直观地构造出所需的辅助函数。

例1.(Lagrange)中值定理。设函数F(x)在［a，b］上连续，在(a，b)内可导，则在(a，b)内至少存在一点ξ，使得

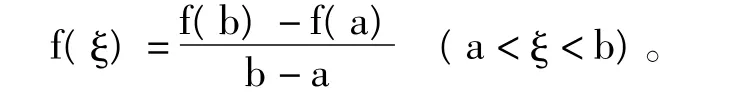
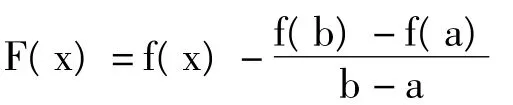
二、利用分析法构造辅助函数

指由结论出发紧扣已知条件一步一步的向已知进行追索，在适当的地方引进辅助函数，使已知和未知联系起来，最后得证。

分析：观察不等式，可以发现，中间部分是对数，左端是分式(当然右端也可以看成分式)而对数的倒数正好是分式，所以我们不难想到借助于(Lagrange)中值定理来证明它。

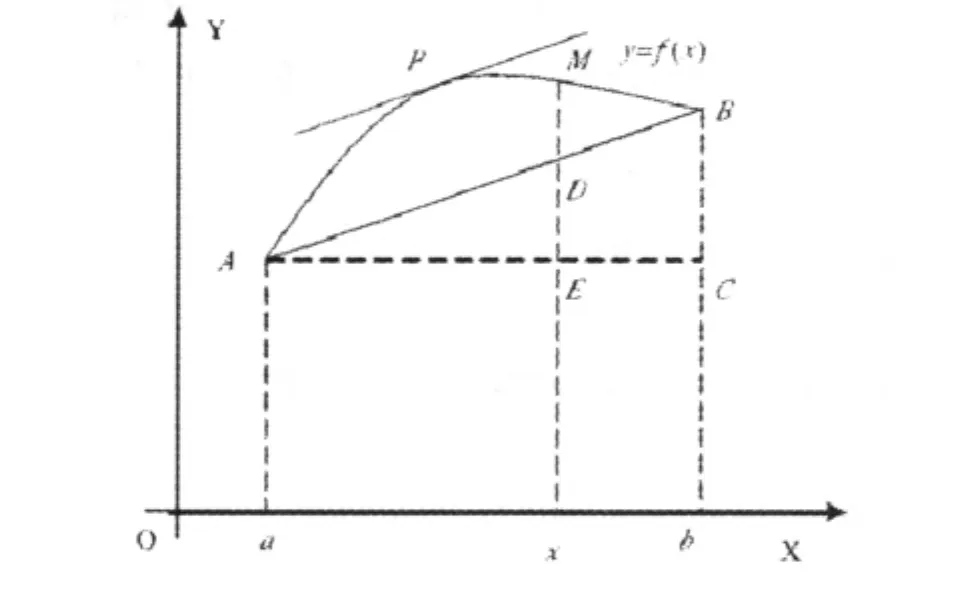
图1

证明：设函数 f(x)=lnx，当 x∈［1，1+x］时，可知该函数满足(Lagrange)中值定理的条件，所以存在一点ξ∈(1，1+x)

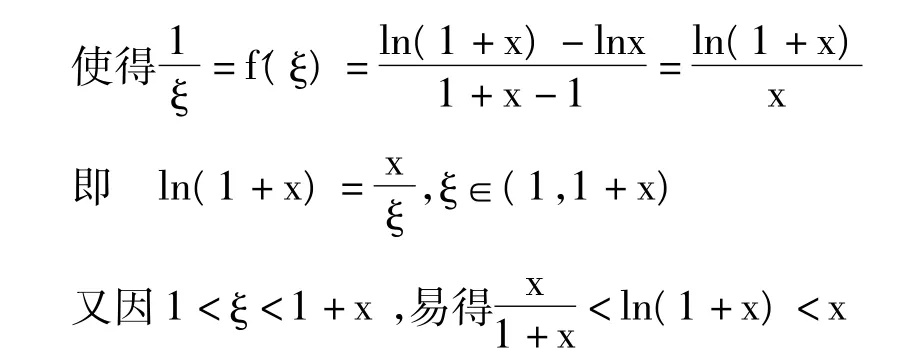
另外辅助函数也可以设为f(x)=ln(1+x)，这时要在［0，x］上证明。

三、利用积分上限函数作为辅助函数

在许多关于定积分的命题或结论的证明中，经常利用积分上限函数作为辅助函数，尤其是在牛顿一莱布尼兹公式的证明中，运用的非常巧妙。

例3.牛顿一莱布尼兹公式的证明

四、利用已知函数构造辅助函数

利用已知函构造出一个新的函数通过适当整理，而由需要求出一些特殊的函数值。

例4.计算ln2的近似值

解此题时，如果设辅助函数为f(x)=ln(1+x)，把他展成麦克劳林级数，并且取x=1得：

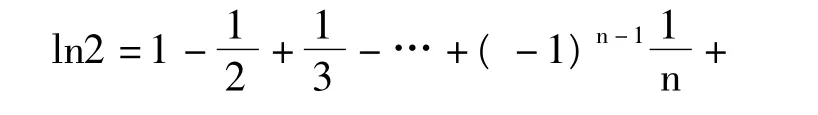
这种方法虽然能求得ln2的近似值，但这个级数收敛特别慢，如果想要使误差小于10－2，要计算100项之和，如果想要使误差小于10－5，要计算十万项之和，这在实际中是不可能的。所以如果没这个函数帮助解题就不当。但想到

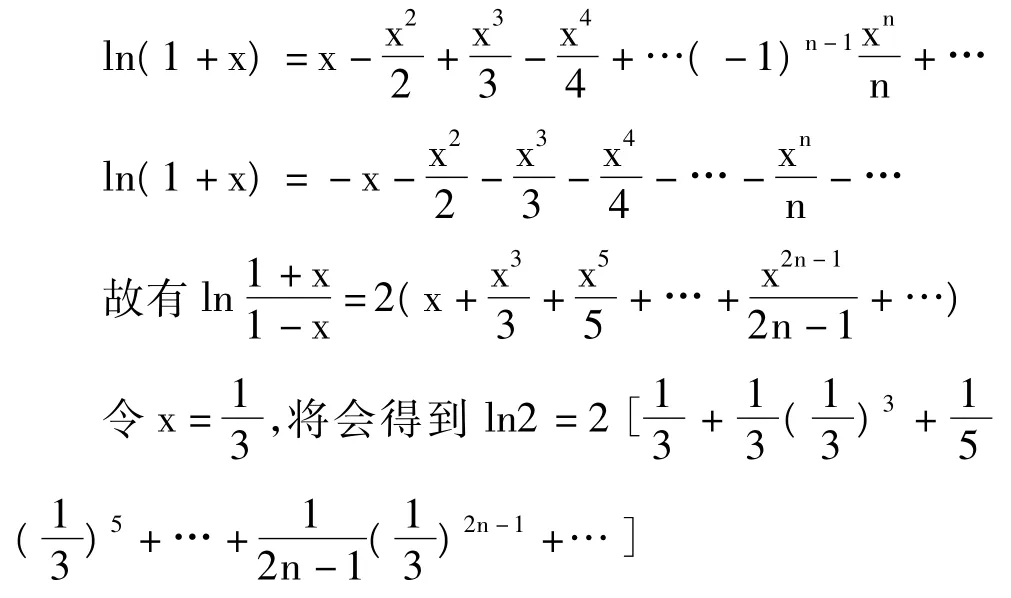
对于这个式子来说，只需取几项就能得到相当好的近似值，由上例子可以看出，对于有些题，我们可以找出不止一个辅助函数。

通过以上的例子可以看出，这些被构造出来的辅助函数与所论命题有着直接或间接关系，在平时教学中被轻描淡写地一带而过。如果在教学中能加强对构造辅助函数的研究对于开阔高职学生的思路，培养他们的创新意识和分析问题、解决问题的能力具有十分重要的意义。

［1］同济大学数学教研室主编.高等数学：上、下册.北京：高等教育出版社1989

［2］刘玉琏，傅沛仁.数学分析讲义(第5版)［M］.北京：高等教育出版社，2008：4～7.

［3］解恩泽、徐本顺.数学思想方法.济南：山东教育出版社，1998

Auxiliary Function Application in Higher Vocational Mathematics Teaching

HE Run－min
(Shaanxi Polytechnic Insitiute，Xianyang Shaanxi，712000)

In the teaching of mathematics in higher vocational education，it is very common to structure an auxiliary function to solve mathematical problems.The study of structuring the auxiliary function has the extremely vital significance for students to broaden their thinking，cultivate their innovation consciousness and the abilities to analyze and solve questions.

structured approach;auxiliary function;method of thinking

G642 < class="emphasis_bold">文献标识码：A

A

1671－3974(2012)02－0068－02

2012－03－14

何润民(1961－)，男，硕士，陕西工业职业技术学院(基础部)讲师。研究方向：数学理论教学。