n维超长方体中图形函数的计数

李应，吴康

(华南师范大学数学科学学院，广东广州 510631)

n维超长方体中图形函数的计数

李应，吴康

(华南师范大学数学科学学院，广东广州 510631)

利用组合几何计数原理和方法，研究在均匀分割的n维超长方体中，所有n维超长方体的任一k维测度和的计数问题.从顶点和、周长和、面积和等低维测度和计数方法入手，然后类比迁移到高维空间中，最终得到任一k维测度和的计数公式，并在五种特殊n维超长方体中推广.

组合几何计数;n维超长方体;图形函数;k维测度;k维测度和

1 问题引入

“在一条线段上添加n个分点，求所有线段的条数”、“在m×n棋盘中，求所有长方形的个数”这类几何图形中求某种图形个数的问题常见于文献［1－2］.直线、平面或空间图形均匀分割求个数问题前人已经推导出具体计算公式.本文研究n维超长方体经均匀分割后，所有n维超长方体的任一k维测度和的计数问题，并在五种特殊n维超长方体中作进一步推导.

本文约定所有图形在n维欧氏空间［3］内讨论，并作如下定义.

对k维面约定k=0时称为顶点;k=n时即Tn(A)本身;k=1时称为一维棱，第i维的一维棱简称为ai边.

对k维测度约定0维测度等于1.

定义3在Tn(A)中，顶点、一维棱、二维面、三维面、…、n维面称为Tn(A)的元素.同一维度的元素称为同种元素，如长方形的6个面是同种元素，12条棱也是同种元素.

定义4在Tn(A)中，与任一k维面测度相等的同种元素个数记为h(n，k).

引理1在Tn(A)中，与任一k维面测度相等的同种元素个数

证明在k维面为1，2，…，n的任意排列)中，xik+1，xik+2，…，xin的每个值都有两种选择，由乘法原理易得:h(n，k)=2n－k.

定义5若Tn(A)被均匀分割为m1×m2×…×mn等分(mi∈N+，mi与ai边对应，i=1，2，…，n)，则用Tn(a1，a2，…，an; m1，m2，…，mn)表示，简记为Tn(A;M)，其中M表示向量(m1，m2，…，mn).

定义6在Tn(A;M)中，所有n维超长方体的个数用g(M)表示.

特别地，在均分为m段的线段中，所有线段条数用g(m)表示.

定义7在Tn(A;M)中，设1≤j1＜j2＜…＜jk≤n，那么从aj1，aj2，…，ajk对应k边上各取定一条线段，则一类n维超长方体的一个k维面被确定，这类n维超长方体的个数记为g(m1，m2，…，mn;mj1，mj2，…，mjk).

引理2定义7中n维超长方体的个数

证明定义7中n维超长方体，由不是第j1，j2，…，jk的基维上任意取一条线段而确定，由定义6易得(2)式成立.

引理3［1］在Tn(A;M)中，所有n维超长方体的个数

定义8用fn，k(A;M)表示Tn(A;M)中所有n维超长方体的所有k维测度和，如所有1维测度和即周长和，所有2维测度和即表面积和.

引理4［1］在Tn(A;M)中，所有n维超长方体的0维测度(顶点个数)和

2 一维测度图形函数的计数

2.1 f1，1(a1;m1)的计数公式

定理1［4］如图1所示，线段AB的长度为a1，均分为m1段，则线段AB中所有线段长度之和为

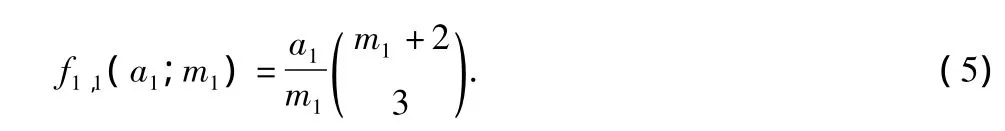
图1 线段ABFig.1Line AB

证明线段AB均分为m1段，则AB间共有m1+1个点，那么长度为·i(1≤i≤m1)的线段数量有m1+1－i条.因此

2.2 f2，1(a1，a2;m1，m2)的计数公式

定理2如图2所示，长方形ABCD中，AB长为a1，均分为m1段，AD长为a2，均分为m2段，长方形ABCD平行分割为m1×m2棋盘，则长方形ABCD中所有长方形的周长之和为

图2 长方形ABCDFig.2Rectangle ABCD

证明长方形ABCD中有两组平行线，图中任一小长方形由两对平行线相交而成，且为一一对应关系.长方形ABCD中所有长方形的周长之和，可分为平行于AB的线段和l1，平行于AD的线段和l2这两部分.以下首先讨论l1:在AB上任意取定一条线段，不妨取EF，则一类长方形的一组对边长度被确定，另一组对边长度由AD决定，故这类长方形个数与线段AD上所有线段条数相等，即g(m2).由定理1，AB上所有线段和为f1，1(a1;m1)，因此l1=f1，1(a1;m1)·h(2，1)·g(m2).同理l2=f1，1(a2;m2) ·h(2，1)·g(m1).故

其中f2，1(a1，a2;m1，m2)为T2(a1，a2;m1，m2)中所有长方形的周长(1维测度)和.

2.3 f3，1(a1，a2，a3;m1，m2，m3)的计数公式

定理3如图3所示，长方体ABCD－A'B'C'D'中，AB长为a1，均分为m1段，AD长为a2，均分为m2段，AA'长为a3，均分为m3段，长方体ABCD－A'B'C'D'被m1×m2×m3等分，则长方体ABCD－A'B'C'D'中所有长方体周长之和为

证明长方体ABCD－A'B'C'D'中有3组平行面，图中任一小长方体由3对平行面相交而成，且为一一对应关系.长方体ABCD－A'B'C'D'中所有长方形的周长之和，可分为平行于AB的线段和l1，平行于AD的线段和l2，平行于AA'的线段和l3这3部分.以下首先讨论l1:在AB上任意取定一条线段，不妨取EF，则一类长方体的一组对边长度即被确定，另外两组对边由AD与AA'决定，故这类长方形的个数为g(m1，m2，m3;m1).由定理1，AB上所有线段和为f1，1(a1;m1)，因此l1=f1，1(a1;m1)·h(3，1)·g(m1，m2，m3;m1).

图3 长方体ABCD－A'B'C'D'Fig.3Cuboid ABCD－A'B'C'D'

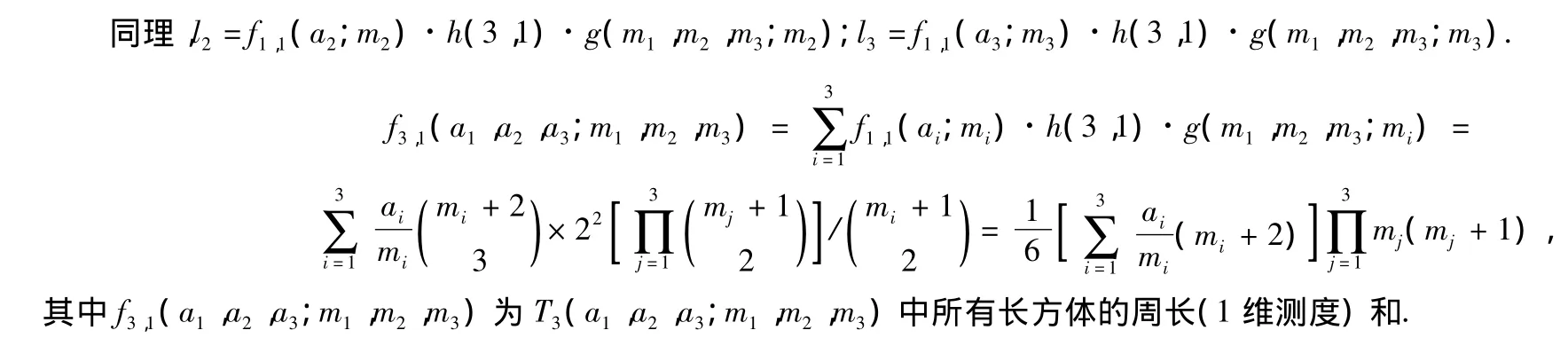
2.4 fn，1(A;M)的计数公式

定理4Tn(A;M)中，所有n维超长方体的周长(1维测度)之和

证明Tn(A;M)中有n组平行面，任一小n维超长方体由n对平行面相交而成，且为一一对应关系.fn，1(A;M)可分为平行于各ai(i=1，2，…，n)边的线段和li，共n部分.以下任取lk(1≤k≤n)进行讨论.

设ak对应的边为HM，在线段HM上任意取定一条线段，则一类n维超长方体的一组对边长度被确定，另外(n－1)组对边由其余a1，a2，…，ak－1，ak+1，…，an对应的(n－1)条边决定，故这类n维超长方体个数为g(m1，m2，…，mn;mk).由定理1，HM上所有线段和为f1，1(ak;mk)，因此lk=f1，1(ak;mk)·h(n，1)·g(m1，m2，…，mn;mk).

至乾隆七年，乾隆皇帝为智朴修进士坟，估算智朴和尚大概活了一百岁。 无论是记录智朴曲折心路历程的《青松红杏图》、体现其诗文造诣的《盘山志》，还是与皇帝士子的结交来往，都使智朴跌宕的人生充满传奇色彩。 关于智朴的研究，还有很多未解之疑，待再作详论。

其中fn，1(A;M)为Tn(A;M)中所有n维超长方体的周长(1维测度)和.

3 二维测度图形函数的计数

3.1 f2，2(a1，a2;m1，m2)的计数公式

定理5如图2所示，长方形ABCD中，AB长为a1，均分为m1段，AD长为a2，均分为m2段，长方形ABCD平行分割为m1×m2棋盘，则长方形ABCD中所有长方形面积和为

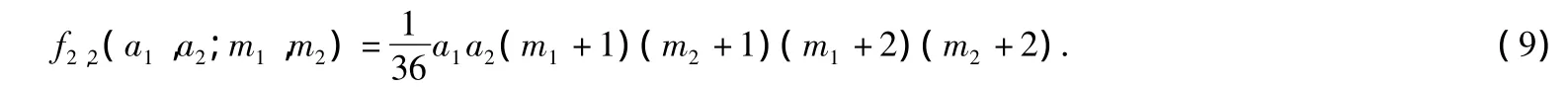
证明长方形ABCD中任一小长方形由AB、AD这两条边上，各边适当取一条线段即可确定.因此，在AB上任意取定一条线段，不妨取EF，则一类长方形的一组对边长度lEF即被确定，另一组对边长度由AD决定.故这类长方形的面积和为:lEF· f(a2，m2).由定理1，AB上所有线段和为f1，1(a1;m1)，则长方形ABCD中所有长方形的面积和为

其中f2，2(a1，a2;m1，m2)为T2(a1，a2;m1，m2)中所有长方形的面积(2维测度)和.

3.2 f3，2(a1，a2，a3;m1，m2，m3)的计数公式

定理6如图3所示，长方体ABCD－A'B'C'D'中，AB长为a1，均分为m1段，AD长为a2，均分为m2段，AA'长为a3，均分为m3段，长方体ABCD－A'B'C'D'被m1×m2×m3等分，则长方体ABCD－A'B'C'D'中所有长方体的表面积之和为

证明长方体ABCD－A'B'C'D'中任一小长方体由AB、AD、AA'这三条边上，各边适当取一条线段确定.任取AB、AD、AA'的两边，每边取一条线段，则可确定一类长方体h(3，2)个面的面积.不妨取AD、AA'，由定理5，AD与AA'中所有长方体的面积和为f2，2(a2，a3;m2，m3).由于每一个面积对应一类长方体个数为g(m1).因此，

3.3 fn，2(A;M)的计数公式

定理7Tn(A;M)(n≥2)中，所有n维超长方体的2维测度(表面积)之和

证明Tn(A;M)中任一小n维超长方体，由a1，a2，…，an对应n条边，各边适当取一条线段确定.任取a1，a2，…，an对应两边，每边取一条线段，可确定一类n维超长方体h(n，2)个面的面积.不妨取aj1，aj2对应边，由定理5，这两边所决定的所有长方体面积和为f2，2(aj1，aj2;mj1，mj2).由于每一个面积对应一类长方体个数为g(m1，m2，…，mn;mj1，mj2).故

其中fn，2(A;M)为Tn(A;M)中所有n维超长方体的2维测度(表面积)和.

4 三维测度图形函数的计数

4.1 f3，3(a1，a2，a3;m1，m2，m3)的计数公式

定理8如图3所示，长方体ABCD－A'B'C'D'中，AB长为a1，均分为m1段，AD长为a2，均分为m2段，AA'长为a3，均分为m3段，长方体ABCD－A'B'C'D'被m1×m2×m3等分，则长方体ABCD－A'B'C'D'中所有长方体的体积之和为

证明长方体ABCD－A'B'C'D'中，由AB、AD两边各取一条线段可确定一类小长方体的底面积S1，而这类小长方体的高则由AA'上任取一条线段即可，故这类小长方体的体积之和为S1·f(a3，m3).由定理5，AB、AD所决定棋盘里，所有长方体的面积和为f2，2(a1，a2;m1，m2)，则长方体ABCD－A'B'C'D'中所有长方体的体积和为

其中f3，3(a1，a2，a3;m1，m2，m3)为T3(a1，a2，a3;m1，m2，m3)中所有长方体的体积(3维测度)和.

4.2 fn，3(A;M)的计数公式

定理9Tn(A;M)(n≥3)中，所有n维超长方体的3维测度之和

证明Tn(A;M)中任一小n维超长方体，由a1，a2，…，an对应n条边上，各边适当取一条线段确定.任取a1，a2，…，an对应的三边，每边取一条线段，则可确定一类n维超长方体h(n，3)个3维面.不妨取aj1，aj2，aj3对应边，由定理8，aj1，aj2，aj3对应边所决定的所有3维测度和为f3，3(aj1，aj2，aj3;mj1，mj2，mj3)，由于每一个3维面对应一类n维超长方体的个数为g(m1，m2，…，mn;mj1，mj2，mj3).因此，

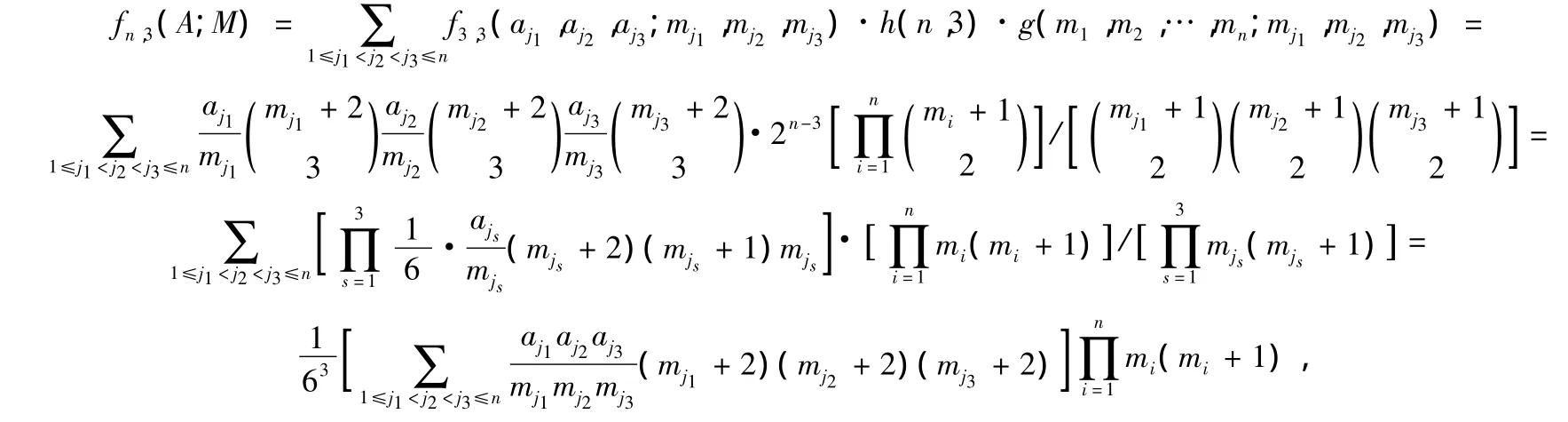
其中fn，3(A;M)为Tn(A;M)中所有n维超长方体的3维测度和.

5 k维测度图形函数的计数

5.1 fn，n(A;M)的计数公式

引理5在Tn(A;M)中，所有n维超长方体的n维测度之和

证明以下用数学归纳法证之.

当n=k+1时，在Tk+1(a1，…，ak+1;m1，…，mk+1)中，由a1，a2，…，ak对应的k边各取一条线段可确定一类小(k+1)维超长方体的k维测度Sk，而这类小(k+1)维超长方体在第(k+1)维上的大小由ak+1对应边上任取一条线段决定，故这类小(k+ 1)维超长方体的(k+1)维测度和为Sk·f(ak+1，mk+1).由归纳假设a1，a2，…，ak对应边所组成图形中，所有k维超长方体的k维测度和为fk，k(a1，a2，…，ak;m1，m2，…，mk).因此

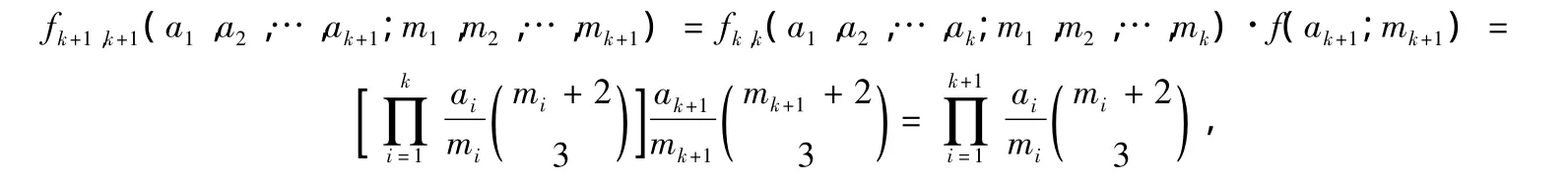
即n=k+1命题成立.故原命题得证.

5.2 fn，k(A;M)的计数公式

定理10在Tn(A;M)中，所有n维超长方体的k(0≤k≤n)维测度之和

证明Tn(A;M)中任一小n维超长方体，由a1，a2，…，an对应n条边各适当取一条线段确定.任取a1，a2，…，an对应的k边，每边取一条线段，则可确定一类n维超长方体的h(n，k)个k维面.不妨取aj1，aj2，…，ajk所对应边，由引理4，Tk(aj1，aj2，…，ajk;mj1，mj2，…，mjk)中所有k维超长方体的k维测度和为fk，k(aj1，aj2，…，ajk;mj1，mj2，…，mjk).由于每一个k维面确定一类n维超长方体个数为g(m1，m2，…，mn;mj1，mj2，…，mjk).因此

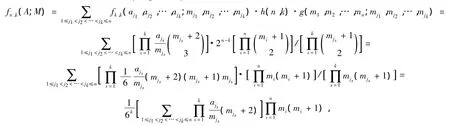
其中fn，k(A;M)为Tn(A;M)中所有n维超长方体的k维测度和.

约定k=0时，

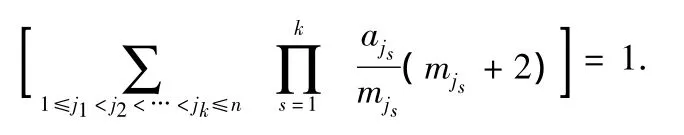
6 特殊的均匀分割下图形函数的计数

前面在一般的n维超长方体中推导出fn，k(A;M)的计算公式，下面通过A，M的特殊取值，利用代入化简的方法，给出5种特殊均匀分割下定理10的几个重要推论.

［1］柳柏濂.几何组合计数趣谈［M］.广州:广东教育出版社，1988:1－18.

［2］冯跃峰.棋盘上的组合数学［M］.上海:上海教育出版社，1998:183－219.

［3］张禾瑞，郝鈵新.高等代数［M］.4版.北京:高等教育出版社，2007:310－335.

［4］柳柏濂，吴康.竞赛数学的原理和方法［M］.2版.广州:广东高等教育出版社，2005:184－206.

The Counting of Graphical Functions in n-Dimensional Super-Cuboids

LI Ying，WU Kang

(School of Mathematics Science，South China Normal University，Guangzhou 510631，China)

By means of the principles and methods of combinatorial geometric counting，the enumeration problems of the total measures for any k-dimension of n-dimensional super-cuboids under uniform partition are studied.It starts from the enumeration methods of low dimensional total measures，such as vertices summation，perimeter and total area，then compares and transfers the methods to higher dimensional space.Finally，it gets the enumeration formula for the total measures of any k-dimension of the super-cuboids，and promotes into five special kinds of n-dimensional super-cuboids.

combinatorial geometric counting;n-dimensional super-cuboid;graphical function;k-dimensional measure;k-dimensional total measures

O157.3

A

1007－0834(2012)02－0024－05

10.3969/j.issn.1007－0834.2012.02.007

2012－02－23

李应(1987—)，男，广东高州人，华南师范大学数学科学学院在读硕士研究生.