具资源效应的非对称“鹰鸽博弈”进化稳定分析
刘奇龙 #, 贺军州 # , 杨 燕, 王亚强,2, 高 磊,2, 李耀堂, 王瑞武,*
(1. 中国科学院昆明动物研究所, 昆明 650223; 2. 云南大学 数学与统计学院, 昆明 650091;
3. 云南中医学院 现代教育技术中心,昆明 650500; 4. 云南财经大学 统计与数学学院,昆明 650221)
具资源效应的非对称“鹰鸽博弈”进化稳定分析
刘奇龙1,2,3,#, 贺军州1,4,# , 杨 燕1, 王亚强1,2, 高 磊1,2, 李耀堂2,*, 王瑞武1,*
(1. 中国科学院昆明动物研究所, 昆明 650223; 2. 云南大学 数学与统计学院, 昆明 650091;
3. 云南中医学院 现代教育技术中心,昆明 650500; 4. 云南财经大学 统计与数学学院,昆明 650221)
解释合作行为的演化一直是生命科学及社会学研究的重要问题之一。经典理论研究大都关注于合作双方对等的情况。然而,在合作系统中的合作双方通常是不对等的, 由此可带来博弈双方支付的非对称并影响合作双方的合作行为。该文基于经典的“鹰鸽博弈”模型, 同时考虑非对称性相互关系和资源压力的影响, 建立了具有强弱之分的四策略 (实力强且合作、实力强且不合作、实力弱且合作和实力弱且不合作) 非对称博弈模型。结合演化博弈理论及动力系统稳定性理论分析发现:在系统达到稳定状态时, 四种策略的比例变化显著地依赖于博弈双方的强弱之比、资源压力及冲突的单位成本收益。对模型的进一步分析显示, 当资源充足时, 实力强且合作的比例与冲突的单位成本收益负相关;而实力强且不合作、实力弱且不合作的比例都与冲突的单位成本收益正相关,并且随着系统强弱对比增加, 实力强且合作及实力强且不合作的比例均增加, 而实力弱且不合作的比例将减小。当资源短缺时, 模型得出一个有趣的结论, 即随着博弈双方的强弱之比的变化, 经典的“智猪博弈”与“鹰鸽博弈”可相互转化, 该结论将能为不同均衡状态之间的相互转化给出一个动力学解释。
非对称; 鹰鸽博弈; 复制动态方程; 进化稳定策略; 智猪博弈
对合作行为演化机制的探讨是生物学、社会学和经济学中一个尚未完全解决的重大问题(Axelrod,1984; Dopfer et al, 2004; Frank, 1998; West et al,2007; Ye et al, 2005)。由 John Maynard Smith 创立的进化博弈理论(Maynard Smith, 1982)为博弈理论的发展注入了活力, 并为研究系统内个体的合作问题奠定了方法学基础。基于演化博弈理论基础并利用“鹰鸽博弈”模型, John Maynard Smith (Maynard Smith, 1982)的研究发现:局中人采取混合策略(p, (1 −p) )是该系统的进化稳定策略, 其中p=v/c(这里合作收益v小于冲突成本c)为博弈局中人采取鹰策略的比例。然而, 在现实的合作系统中, 博弈双方不会一直处于唯一的一种稳定均衡状态, 而会因为遗传突变、公共资源的变化等因素而调整自己的策略(Boyd, 2006; Boyd & Lorberbaum,1987; Heinsohn & Packer, 1995; Hauert & Doebeli,2004; Wang et al, 2008), 从而均衡状态可能被打破,并随之建立新的均衡状态。
经典的“鹰鸽博弈”理论模型不能解释多种均衡状态之间的相互转化, 出现这种困境的原因很可能是经典模型仅考虑了博弈双方对等的情况。而在现实的合作系统中, 博弈双方大都具有非对称性相互关系, 比如蜂后(queens)与工蜂(workers)、猴王与次级猴、双亲与子代、强者与弱者、雌性与雄性等(Maynard Smith, 1982)。大量的实验观测及数据分析显示,几乎所有的经典合作模式系统都存在着不同程度的非对称性相互关系(Heinsohn & Packer,1995; Reeve, 1992; Wang et al, 2009, 2010, 2011),这种非对称相互关系, 很可能是不同均衡状态之间相互转化的本质原因。
本文基于经典的“鹰鸽博弈”模型, 同时考虑非对称性相互关系和资源压力的影响, 建立了具有四策略(实力强且合作、实力强且不合作、实力弱且合作和实力弱且不合作) 的非对称博弈模型。结合演化博弈理论及动力系统稳定性理论分析该系统的演化行为发现:在系统达到稳定状态时, 四种策略的比例变化显著地依赖于博弈双方的强弱之比,资源压力及冲突的单位成本收益。同时发现, 当资源短缺时, 随着博弈双方的强弱之比的变化, 经典的“智猪博弈”将与“鹰鸽博弈”之间形成相互转化关系, 从而为合作系统的不同均衡状态之间相互转化给出了一个动力学解释。
1 建立模型
1.1 “鹰鸽博弈”模型回顾
假设两个理性群体(或个体), 它们都有两个策略:鹰策略(H)和鸽策略(D), 于是博弈双方有四个策略组合:(D,D)、(D,H)、(H,D)、(H,H)。在博弈中为了获得某一收益v, 若博弈双方都采取鹰策略H, 则双方应付出冲突成本c, 双方各自的纯收益均为(v−c)/2; 若博弈双方采取的策略不同,则采取鹰策略方的纯收益为v, 而采取鸽策略方的纯收益为0; 若博弈双方都采取鸽策略, 则双方各自的纯收益均为v/2(Maynard Smith, 1982; Drew et al, 2002), 即得如表1所示的对称支付矩阵。
经典的“鹰鸽博弈”暗含了合作系统中博弈双方的实力是对等的, 其理论结果是:当收益大于冲突成本(即v>c)时, 该博弈存在一个纯进化稳定策略(H,H); 而当收益小于冲突成本(即vc)时,该博弈存在一个混合进化稳定策略(p, (1 −p) ), 其中p=v/c为博弈方采取鹰策略的比例(Maynard Smith, 1982; Drew et al, 2002)。而在现实的合作系统中博弈双方的实力一般是不对等的(即实力强弱的非对称)(Heinsohn & Packer, 1995; Reeve, 1992;Wang et al, 2009, 2010, 2011)。在博弈双方实力不对等的条件下, 博弈双方的收益受到双方强弱之比的影响, 即当博弈双方发生冲突且冲突成本大于收益(即c>v)时, 博弈双方受到的伤害程度是不一样的,也即实力强的参与者受到的伤害小于实力弱的参与者。此时博弈双方的总损失(收益)会受到资源压力的影响, 当资源充足时, 总损失(收益)会较小(大),当资源短缺时, 总损失(收益)会较大(小)。而当博弈双方合作时, 对收益的分配是实力强的博弈方得到更高的收益。据此,我们建立如下非对称“鹰鸽博弈”模型。
1.2 非对称“鹰鸽博弈”
考虑实力不对等的博弈双方进行“鹰鸽博弈”, 并且假设博弈双方的实力之比为: :(1 )k−k(假定0.5<k<1, 即前者的实力比后者强), 其中k及1−k可定义为博弈双方所占据的资源或发生冲突时获胜的几率等变量; 冲突成本c大于合作收益v; 当博弈双方都采取鹰策略, 即发生冲突时, 博弈双方所受到的伤害程度受对方实力的影响, 同时总的伤害程度受资源压力a(当a=1时, 表示资源平衡, 当a>1时, 表示资源短缺, 当0<a<1时, 表示资源充足)的影响, 假设此时实力强的一方得到的纯收益为a( 1 −k)(v−c), 实力弱的一方得到的纯收益为ak(v−c), 总收益为a(v−c); 当博弈双方都采取鸽策略, 即合作时, 假设此时实力强的一方得到的纯收益为kv, 实力弱的一方得到的纯收益为(1−k)v; 当双方采取不同的策略时, 假设收益与经典的“鹰鸽博弈”模型相同。根据以上假设, 可以得到如表2所示的非对称支付矩阵。
在具有非对称性的群体中, 每个个体可能扮演两种不同的角色(Wu, 2000) (实力强或实力弱), 且这两种角色分别有两种不同的策略(合作和不合作),两两组合可得四类个体:实力强且合作SC、实力强且不合作SD、实力弱且合作WC和实力弱且不合作WD。为了分析这四类个体在一个系统内的分布情况, 我们虚拟出两个具有四策略(SC、SD,WC和WD)的对称博弈方进行随机选择配对博弈, 当博弈双方同时扮演相同的角色时, 双方的支付矩阵如表 1; 当博弈双方扮演不同的角色时, 双方的支付矩阵如表2。于是得到如表3所示的支付矩阵。

表1 对称鹰鸽博弈支付矩阵Tab. 1 Payoff matrices for the symmetric Hawk-Dove game

表2 非对称鹰鸽博弈支付矩阵Tab. 2 Payoff matrices for the symmetric Hawk-Dove game

表3 四策略支付矩阵Tab. 3 Payoff matrix with four strategies
假设博弈双方在进行“鹰鸽博弈”时, 采取策略SC、SD、WC和WD的个体,占群体的数量比例分别为x1、x2、x3和x4。此时群体中采取策略SC、SD、WC和WD的个体的期望收益分别为:

按照生物进化复制动态理论(Taylor & Jonker,1978; Schuster & Sigmund, 1983), 采用策略收益较低的博弈方会改变自己的策略, 转向(学习或模仿)有较高收益的策略, 因此,群体中采用不同策略个体的数量比例就会发生变化, 特定策略的比例变化速度与其比例和其收益超过平均收益的幅度均成正比。由此得到群体中采用策略SC、SD、WC和WD的比例关于时间t的复制动态方程(Schuster &Sigmund, 1983; Taylor & Jonker, 1978):
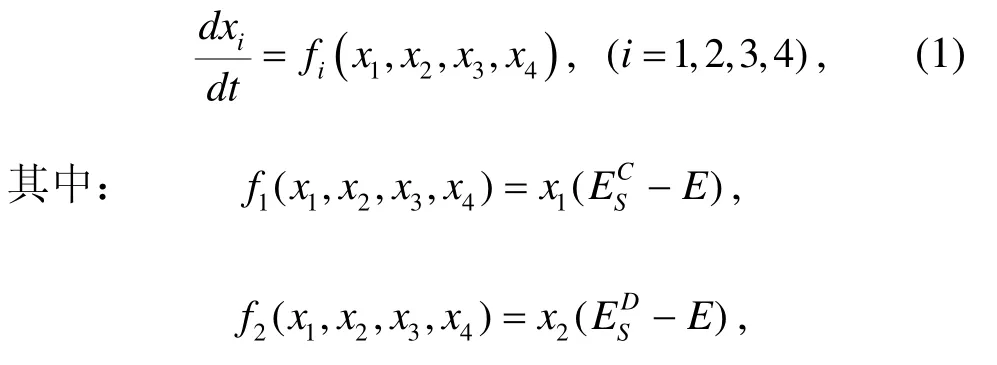


表4 文中符号及定义Tab. 4 Symbols and definitions used in this paper
2 系统稳定性分析
2.1 系统(1)的非负平衡点



考虑到种群中采取某一策略的个体的数量比例不可能为负值, 于是只需分析系统(1)的非负平衡点。
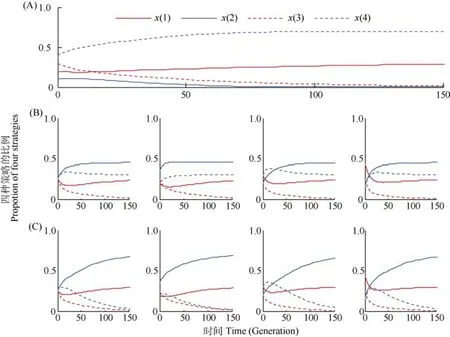
由假设条件v 为分析系统(1)非负平衡点的稳定性, 可以通过求其线性近似系统在平衡点处对应特征方程的特征值, 由特征值的符号来判断在该平衡点处系统的稳定性, 并利用Liapunov函数(Gu, 2000; Zhang &Feng, 2000)来证明E1,E2的全局稳定性。应用此法,我们得到在假设条件v 上是全局稳定的; 当ak> 0.5 >a( 1 −k)时, 非负平衡点E2在 上是全局稳定的(附录2,见本刊网站Supporting info)。 为了清晰显示在不同条件下系统(1)的动力学行为, 下面我们采用 Runge-Kutta-Felhberg算法(Xue & Cheng, 2004)近似求解系统(1), 对该系统的稳定性进行定量说明。 取系统中参数a=2、k=0.6,a( 1 −k) = 0 .8 > 0 .5,数值模拟显示, 当进化达到稳定状态时, 实力强且合作与实力弱且不合作的个体分别以1 − (v/c) = 0.3和v/c= 0 .7的比例共存, 而实力强且不合作与实力弱且合作的个体绝灭(图 1A); 取系统中的参数a= 0 .5、k=0.6, 此时ak= 0 .3 < 0 .5, 数值模拟显示,对于不同的初值, 当进化达到稳定状态时, 实力强且合作、实力强且不合作和实力弱且不合作的个体分别以0.2457、0.4526和0.3017的比例共存, 而实力弱且合作的个体绝灭(图 1B)。而取系统中参数a= 1 、k=0.6, 此时a( 1 −k) = 0.4 < 0.5 < 0.6=ak,数值模拟显示, 对于不同的初值, 当进化达到稳定状态时, 实力强且合作与实力强且不合作的个体分别以1 − (v/c) = 0 .3和v/c= 0 .7的比例共存, 而实力弱且合作与实力弱且不合作的个体绝灭(图1C)。 图1 四种策略的比例随时间的变化Fig. 1 The proportion of four strategies changes with time varying 从上面的分析知, 当ak<0.5时, 平衡点E1是全局稳定点, 而由于我们的前提是k> 0.5, 故参数a需满足a<1, 即资源充足。下面我们将在资源充足的条件下, 讨论资源压力a、强者的实力k和冲突的单位成本收益v/c对平衡点E1对应的各策略比例的影响。 在点E1中x3= 0, 即实力弱且合作的比例为零,显然它与参数a、k和v/c的选取无关, 于是只需讨论a、k和v/c对点E1的其它三个分量的影响。令m=v/c(定义为冲突的单位成本收益), 由上面的求解有因此,x1、x2和x4均可看成a、k、m的函数, 从而得如图2所示的各参数对x1、x2和x4的影响。 由图2可以看出, 随着冲突的单位成本收益m的增大, 实力强且合作(图2 A-C)的比例减小;而实力强且不合作(见图 2 D-F)与实力弱且不合作(图 2 G-I)的比例均增大, 即E1稳定时, 实力强且合作的比例与冲突的单位成本收益负相关;而实力强且不合作、实力弱且不合作的比例均与冲突的单位成本收益正相关。冲突的单位成本收益越大博弈双方越倾向于选择冲突的结论与群体(或个体)趋利本性相符(Hauert & Doebeli, 2004; Maynard Smith, 1982)。通过比较图2各分图横轴变量k对各策略比例的影响发现, 实力强且合作(图 2 A-C)及实力强且不合作(图2 D-F)的比例随k的增大而增大, 但实力弱且不合作(图2 G-I)的比例却随之减小。另外, 当a增大时, 实力强且合作(图 2 A-C)及实力强且不合作(图 2 D-F)的比例均增大, 而实力弱且不合作(图 2 G-I)的比例将会减小。以上结果分析表明,博弈双方的实力之比和资源压力的增大都不利于实力弱的个体的生存。 图2 冲突的单位成本收益与强者的实力k对平衡点E1的影响Fig. 2 Effects of the cost-to-benefit of conflict and strength k of strong player on equilibrium point E1 需要指出的是当a( 1 −k) > 0 .5时, 平衡点E2和E3是局部渐近稳定的(附录 1,见本刊网站Supporting info), 即当四种策略初始比例在平衡点E3附近时, 解曲线才趋于平衡点E3, 而当四种策略初始比例远离平衡点E3时, 解曲线将趋于平衡点E2。有趣的是, 当a( 1 −k) > 0 .5时, 局部渐近稳定点E2和E3的结果恰巧分别对应着经典的“鹰鸽博弈”(Maynard Smith, 1982)和“智猪博弈”(Eric, 2001)的结果。由于在a( 1 −k) > 0 .5条件下平衡点E2和E3是局部渐近稳定的, 因此,我们有必要探讨四种策略的初始值及系统参数与两局部渐近稳定点E2和E3之间的关系。 “智猪博弈”与“鹰鸽博弈”之间的相互转化关系可为不同系统的不同合作形式提供一个合理的解释。比如在狐蒙 (meerkats)社群中, 成员进食时会出现几个个体轮流放哨鸣警(可将个体的合作行为视为混合策略)以防备扑食者(Clutton-Brock et al, 1999), 这正对应着“鹰鸽博弈”的模型结果; 而在意大利蜂(Apis mellifera)社群中, 蜂后(queens)监督惩罚工蜂(workers)产卵(Oldroyd &Ratnieks, 2000; Ratnieks & Visscher, 1989), 这一结果与“智猪博弈”预测的结果一致。导致不同的合作系统出现不同的合作形式可能根源于这些系统具有不同的非对称度, 当具有不同非对称度的合作系统遭遇不同的生境条件时(比如资源短缺时), 我们的研究显示不同的合作系统将可能展现出多样化的合作形式。 Axelrod R. 1984. The Evolution of Cooperation[M]. New York: Basic Books Press. Boyd R. 2006. You have to think different[J].J Evol Biol,19(5): 1380-1382. Boyd R, Lorberbaum JP. 1987. No pure strategy is evolutionarily stable in the repeated prisoner’s dilemma game[J].Nature,327(6117): 58-59. Clutton-Brock TH, O’Riain MJ, Brotherton PNM, Gaynor D, Kansky R,Griffin AS, Manser M. 1999. Selfish sentinels in cooperative mammals[J].Science,284(5420): 1640-1644. Drew F, Jean T, Huang T, Guo K, Gong P, Wang YM, Wang Y, Zhong HJ.2002. Game Theory[M]. Beijing: China Renmin University Press.[Drew F, Jean T, 黄涛, 郭凯, 龚鹏, 王一民, 王勇, 钟鸿钧. 2002.博弈论. 北京: 中国人民大学出版社.] Dopfer K, Foster J, Potts J. 2004. Micro-meso-macro[J].J Evol Econ,14(3):263-279. Eric R. 2001. Games and Information: An Introduction to Game.Theory[M]. 4th ed. Oxford: Basil Blackwell. Frank SA. 1998. Foundations of Social Evolution[M]. Princeton: Princeton University Press. Gu SS. 2000. Ordinary Ddifferential Equations and Dynamical Systems[M].Shanghai: Shanghai Jiaotong University Press. [顾圣士. 2000. 微分方程和动力系统. 上海: 上海交通大学出版社.] Heinsohn R, Packer C. 1995. Complex cooperative strategies in group-territorial African lions[J].Science,269(5228): 1260-1262. Hauert C, Doebeli M. 2004. Spatial structure often inhibits the evolution of cooperation in the snowdrift game[J].Nature,428(6983): 643-646. Maynard Smith J. 1982. Evolution and the Theory of Games[M].Cambridge: Cambridge University Press. Oldroyd BP, Ratnieks FLW. 2000. Evolution of worker sterility in honey-bees (Apis mellifera): how anarchistic workers evade policing by laying eggs that have low removal rates[J].Behav Ecol Sociobiol,47(4): 268-273. Ratnieks FLW, Visscher PK. 1989. Worker policing in the honeybee[J].Nature,342(6251): 796-797. Reeve HK. 1992. Queen activation of lazy workers in colonies of the eusocial naked mole-rat[J].Nature,358(6382): 147-149. Schuster P, Sigmund K. 1983. Replicator dynamics[J].J Theor Biol, 100(3):533-538. Taylor PD, Jonker LB. 1978. Evolutionary stable strategies and game dynamics[J].Math Biosciences,40(1-2): 145-156. Wang RW, He JZ, Wang YQ, Shi L, Li YT. 2010. Asymmetric interaction will facilitate the evolution of cooperation[J].Sci Chin: Life Sci,53(8):1041-1046. [王瑞武, 贺军州, 王亚强, 石磊, 李耀堂. 2010. 非对称性有利于合作行为的演化. 中国科学: 生命科学, 40(8): 758-764.] Wang RW, Ridley J, Sun BF, Zheng Q, Dunn DW, Cook J, Shi L, Zhang YP, Yu DW. 2009. Interference competition and high temperatures reduce the virulence of fig wasps and stabilize a fig-wasp mutualism[J].PLoS One,4(11): e7802. Wang RW, Shi L, Ai SM, Zheng Q. 2008. Trade-off between reciprocal mutualists: local resource availability-oriented interaction in fig/fig wasp mutualism[J].J Anim Ecol,77(3): 616-623. Wang RW, Sun BF, Zheng Q, Shi L, Zhu LX. 2011. Asymmetric interaction and indeterminate fitness correlation between cooperative partners in the fig-fig wasp mutualism[J].J R Soc Interface,8(63): 1487-1496. West SA, Griffin AS, Gardner A. 2007. Social semantics: altruism,cooperation, mutualism, strong reciprocity and group selection[J].J Evol Biol,20(2): 415-432. Wu WK. 2000. Role change in the value net of game theory[J].Nankai Bus Rev,3(5): 18-20. [吴维库. 2000. 竞争博弈中的角色转换. 南开管理评论, 3(5): 18-20.] Xue DY, Cheng YQ. 2004. Advanced Application of MATLAB to Solve Mathematical Problems[M]. Beijing: Tsinghua University Press. [薛定宇, 陈阳泉. 2004. 高等应用数学问题的 MATLAB求解. 北京: 清华大学出版社.] Ye H, Wang DD, Lou WD. 2005. On endogenetic preference for altruism behaviors and its implications to economics[J].Econ Res J,(8): 84-94.[叶航, 汪丁丁, 罗卫东. 2005. 作为内生偏好的利他行为及其经济学意义. 经济研究, (8): 84-94.] Zhang JY, Feng BY. 2000. Geometric and Bifurcation Problems Theory of Ordinary Differential Equations[M]. Beijing: Peking University Press.[张锦炎, 冯贝叶. 2000. 常微分方程几何理论与分支问题. 北京:北京大学出版社.] Evolutionary stability analysis of asymmetric hawk-dove game considering the impact of common resource LIU Qi-Long1,2,3,†, HE Jun-Zhou1,4,†, YANG Yan1, WANG Ya-Qiang1,2, GAO Lei1,2,LI Yao-Tang2,*, WANG Rui-Wu1,* (1.Kunming Institute of Zoology,the Chinese Academy of Sciences,Kunming650223,China; Explaining the evolution of cooperation remains one of the important problems in both biology and social science. Classical theories mainly based on an assumption that cooperative players are symmetrically interacted. However,almost all the well-studied systems showed that cooperative players are in fact asymmetrically interacted and that asymmetric interaction might greatly affect cooperation behavior of the involved players. Considering the asymmetric interaction and the selection pressure of resources, we present a model that possesses four strategies: strengthcooperation (SC), strength-defection (SD), weakness-cooperation (WC) and weakness-defection (WD). Combining evolutionary game theory with dynamical stability theory, we find that the evolutionary results closely depend on the asymmetric interaction and selection pressure of resources as well as cost-to-benefit ratio of conflict. When the common resources are plentiful, the cost-to-benefit ratio of conflict is negatively correlated with the probability of SC, while it is positively correlated with the probability of SD and WD. With increasing the strength ratio between the strong and weak players, the proportion of SC and SD will increase, while the proportion of WD will reduce. The model developed here has intrinsically integrated Boxed Pigs game and Hawk-Dove game. When the common resource is at shortage, the Boxed Pigs game will transform into Hawk-Dove game under the increase of the strength ratio between the strong and weak players. Asymmetric; Hawk-Dove game; Replicator equation; Evolutionarily stable strategy; Boxed pigs game Q332;Q111;O225;F224 A 0254-5853-(2012)04-0373-08 10.3724/SP.J.1141.2012.04373 2011-11-20; 接受日期:2012-04-20 国家自然科学基金资助项目具有P-F性质矩阵及其相关矩阵的性质、算法和应用研究(10961027);合作系统中非对称性和互惠(或亲缘)关系的相互作用研究(71161020)和种间合作系统稳定性维持机制的探讨(31170408) ;云南省自然科学基金(2009CD104); 中国科学院优秀青年科技专项(KSCX2-EW-Q-9)*通信作者(Corresponding author), E-mail: ruiwukiz@hotmail.com; liyaotang@ynu.edu.cn#共同第一作者(Authors contributed equally to the work)2.2 系统(1)非负平衡点的稳定性分析


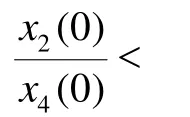
3 结果与讨论



2.School of Mathematics and Statistics,Yunnan University,Kunming650091,China;
3.Modern Education Technology Center,Yunnan University of Traditional Chinese Medicine,Kunming650500,China;4. Statistics and Mathematics College, Yunnan University of Finance and Economics, Kunming650221, China)

