高超声速飞行器多约束多种机动突防模式弹道规划
张科南,周 浩,陈万春
(北京航空航天大学 宇航学院,北京100191)
近年来,随着反导技术的不断进步,机动突防设计成为现代导弹总体设计过程中必不可少的一环.国内外涌现出了许多关于弹道导弹、反舰导弹机动突防技术的研究成果[1~3].这些成果通常集中于研究导弹飞行过程中的某段(如弹道导弹的中段,反舰导弹末端),对该段导弹机动突防制导律进行设计,获得制导律的最优解.
高超声速飞行器具有飞行速度快、射程远和突防能力强等优点.目前,关于高超声速飞行器机动突防模式的成果还很少,本文旨在探讨研究突防技术在这一全新领域的应用.高超声速飞行器因其自身的特点,采用弹道导弹、反舰导弹等传统的机动突防技术效果未必会好.鉴于其速度快、射程远的特点,本文提出了进行大空域机动甚至全程机动的策略.根据飞行任务中的航路点和禁飞区分布[4,5],以及禁飞区类型不同,设计了多种机动突防模式:单S机动、半圆机动、横向蛇形机动、滑翔跳跃机动、纵向蛇形机动.不同机动突防模式的设计问题可以看作是有特定约束要求的弹道优化问题.本文受文献[6]中关于再入机动弹道工程设计法的启发,结合拟平衡滑翔飞行的特点,提出了一种简便易行的直接法优化策略[7],用来求解弹道优化问题.优化过程中,不但考虑了终端条件约束和热流、动压、过载等过程约束,而且加入了航路点和禁飞区的限制.为便于工程实现,还限制了控制变量的变化幅度及变化率.在文献[8]基础上,提出了改进的拟平衡滑翔条件(Improved Quasi-Equilibrium Glide Condition,IQEGC),建立了攻角和倾侧角间一种约束关系,减少了一个控制变量,从而提高了计算速度;而且能够保证弹道的平缓以满足热流、动压、过载等过程约束.
1 研究对象和动力学方程
本文采用国外公开的通用航空飞行器(Common Aero Vehicle,CAV)中的高升力体CAV-H为研究对象,完整的气动参数和结构参数参考文献[9]的附录.采用1976美国国家标准大气模型.
本文设计的是CAV的滑翔段弹道.初始条件为主动段结束后,经过一定变轨,满足起滑点要求的条件.终端条件为满足下压段交班要求的条件.
假设地球为球体,不考虑地球自转的影响,三自由度质点动力学方程为

式中:r为地心到飞行器质心的距离;θ,φ分别为经度和纬度;v为对地速度;FD,FL为阻力和升力,即FD=ρv2SrefCD/2,FL=ρv2SrefCL/2,其中,Sref为飞行器气动参考面积,CD,CL分别为阻力系数和升力系数;γ,σ,ψ分别为当地航迹角、倾侧角和航向角.
2 约束条件
本文考虑了复杂的约束条件,包括控制约束、边界条件和各种过程约束:热流、过载、动压、航路点和禁飞区等.
2.1 控制约束
CAV的2个控制变量为倾侧角σ和攻角α.为了保证飞行器的飞行稳定,设定倾侧角的变化极限是±50°,攻角范围5°~20°,另外,对控制量变化率也进行约束,要求倾侧角变化率不超过10(°)/s,攻角变化率不超过5(°)/s.
2.2 边界条件
为满足起滑点要求,初始条件设为高度h0=60km,速度v0=7km/s,弹道倾角γ0=0°,弹道偏角ψ0=90°.终端约束条件包括目标点的位置和指定的高度、速度限制等.为了满足下压段的交班条件,规定滑翔段末端的速度为2 km/s左右,高度为30~40km.
2.3 热流约束

2.4 过载约束

式(8)左边为飞行器受到的法向气动过载,右边为飞行器可以承受的最大过载,取nT,max=2.5g,g为当地的重力加速度.
2.5 动压约束

式中,ρ为大气密度;qmax为飞行器可以承受的最大动压值,取qmax=60kPa.
2.6 航路点约束
航路点是指飞行器在飞行途中必须经过的一些位置点,进行导航信息确认、侦查拍照或者投递物品等.设第i个航路点的位置(xi,yi),对飞行器要求在某一时刻ti,须有

2.7 禁飞区约束
禁飞区主要指预警雷达扫描区或其他防御系统的保护区域等.本文将禁飞区分为2类,可以避让的禁飞区和无法避让的禁飞区.可避让禁飞区可以简化为无限高圆柱体型和有限高半球型.前者对应预警雷达扫描范围,要想避让该区域,只能从扫描雷达的盲区飞行;后者对应有射程和射高限制的反导系统作用区域,例如美国的爱国者系统,由于其反导导弹的射高受限制,也可以从该区域的上面飞过.对可避让的禁飞区,要保证飞行过程中飞行器距离禁飞区中心在安全范围以内,即

第j个禁飞区的半径为Rj,中心坐标(xj,yj);飞行器到禁飞区中心的距离,x方向上Δxj=xxj,y方向上Δyj=y-yj.
第二类为无法避让的禁飞区,如果目标位于禁飞区的中心,则无论如何都是没办法避让的,这时需要通过一定的机动,改变弹道形状,加大防御系统的拦截难度.
3 拟平衡滑翔条件
升力体飞行器的大部分再入弹道,弹道倾角γ通常很小,并且变化相对较慢.在式(5)中,令cosγ=1,=0,得:

这就是拟平衡滑翔条件QEGC.理论上,只要升力足够,式(12)就可以保证弹道绝对平直.但实际上,随着飞行时间变长,速度越来越小,由于攻角有上限制约,飞行器获得的升力不能满足式(12)时,<0,弹道倾角γ会出现一个快速的下滑,不利于飞行器的稳定控制.本文对式(12)进行了一定的修正,给出改进的拟平衡滑翔条件(Improved Quasi-Equilibrium Glide Condition,IQEGC):

式中,ε是绝对值很小的负数,用来使弹道倾角γ很缓慢地变小,避免出现γ的快速下滑,保证飞行器的稳定.另外,ε可以作为一个优化变量参与弹道设计,通过设计ε,可以得到满足指定终端条件要求的弹道.
由于FL=ρv2SrefCL/2,而CL是攻角α的函数,可见,QEGC提供了2个控制量倾侧角σ和攻角α的约束关系.若已知σ可以用σ来表示α,反之亦然.这个关系式用在优化过程中可以减少优化变量,提高优化效率.
4 最优控制问题的求解
根据参数化方法的不同,求解最优控制问题的直接法分为2种基本类型[10]:①离散控制变量,将连续空间的控制变量参数化,状态变量由数值积分获得;②同时离散控制变量和状态变量,通过若干数学变换将连续动力学微分方程转换为代数方程.本文提出的方法属于第一类直接法.由于飞行器按照QEGC飞行,选取倾侧角作为独立优化变量,攻角可根据式(13)得到,反之亦然.按照航路点和禁飞区的分布,以及禁飞区类型的不同,将倾侧角或攻角离散为分段常值函数,段数的多少根据机动突防模式决定.取每一段的幅值和持续时间作为离散后的优化变量,然后利用序列二次规划(Sequential Quadratic Programming,SQP)方法进行求解.例如,如果要躲避一个禁飞区并返回射面,只需要将倾侧角分为两段,两段的倾侧角符号相反.选择每段的倾侧角幅值和持续时间作为优化变量即可.离散后的倾侧角为
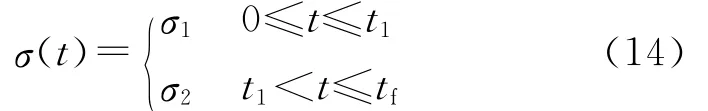
5 多机动突防模式弹道设计
不同的作战任务,对应不同的机动弹道.本文主要根据不同航路点和禁飞区的分布,以及禁飞区类型的不同,设计相应的机动弹道.其中航路点是必须经过的位置点.禁飞区分为可避让和不可避让2种情况.故文中将机动弹道分为横向机动方式和纵向机动方式.
为了便于说明问题,不失一般性,假设CAV的初始位置经纬度为(0°,0°),目标位于赤道平面内.CAV和目标之间存在若干禁飞区和航路点.
5.1 横向机动方式
5.1.1 单S机动
假设在飞行器和目标点中间存在2个半径为400km的禁飞区,中心分别位于经纬度(40°,0°)和(70°,0°)处.其余约束条件如第3节所述.由于2个危险区间隔较远,飞行器可以从2个危险区中间穿过击中目标.假设目标位于赤道平面,经度未指定.以纵程最大作为优化目标函数,将倾侧角σ离散为三段常值函数,相邻两段符号相反,以每段的幅值和持续时间为优化变量.考虑倾侧角变化率的约束,设定倾侧角从一段常值转换到另一段常值的过渡时间tf=10s,这样可以保证倾侧角的变化率不超过10(°)/s.离散后的倾侧角为

式中,σ1,σ2,σ3是常数,表示每一段上倾侧角的幅值,相邻2个符号相反.因为攻角的变化范围比倾侧角小得多,故只要倾侧角满足了变化率约束,攻角自然也满足.
将σ1,σ2,σ3,t1,t2,tf作为优化变量,利用 SQP方法求解转换后的非线性规划问题,结果如图1~图3所示.

图1 单S机动轨迹地面投影
从图1可以看出,优化得到的轨迹成功地避开禁飞区击中目标.从图2中的速度和高度曲线可以看出,轨迹满足终端约束条件.图3中控制变量倾侧角σ和攻角α的变化都在控制边界内.σ变号过程,σ的绝对值先变小后变大,故根据QEGC决定的攻角α也伴随出现先小后大的一种现象,反映在图3中,每次倾侧角σ变号,攻角α出现一个向下的小跳跃.同理可解释图2中弹道倾角γ小跳跃.倾侧角σ变号以后,其幅值往往也发生变化,对应的攻角α也会出现比较明显的变化.图4显示机动弹道始终位于飞行走廊内部,即驻点热流、法向过载和动压都满足约束要求,这是按照QEGC飞行的优点之一.
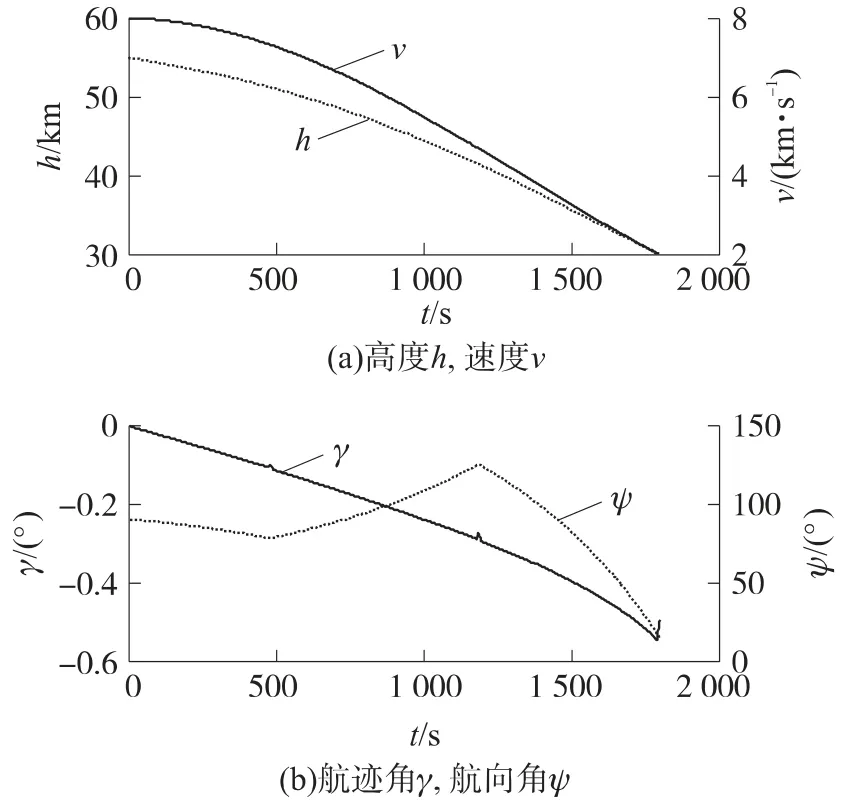
图2 单S机动状态变量

图3 单S机动控制变量
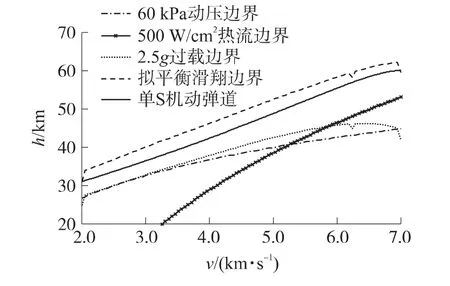
图4 单S机动飞行走廊
单S机动还适用于既要经过航路点,又要避开禁飞区的情况,如图5所示.
相关研究表明,影响数控机床热变形误差的主要原因是主轴部件热变形误差,由于实验条件有限,并且这篇论文主要是验证LWT-LSSVM建模预测方法的可行性与准确性,所以只对数控机床部分发热部件进行实验分析和研究。

图5 单S机动过航路点轨迹地面投影
5.1.2 半圆机动
假设在5.1.1中的2个禁飞区中间(55°,0°)处增加一个半径1 000km的大禁飞区,此时,从中间穿过禁飞区的方式难以实现,可以通过一次大空域半圆机动躲过所有禁飞区.结果如图6和图7所示,图中图形的含义与5.1.1中相似.
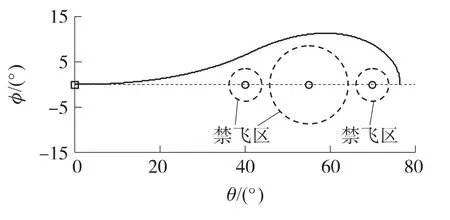
图6 半圆机动轨迹地面投影

图7 半圆机动控制变量
5.1.3 横向蛇形机动
前面几种机动方式都是针对可以避让的禁飞区给出的方案,如果目标位于防御区中心,此时仅靠避让飞行是无法击中目标的.为了以更高的概率突破敌方防御,命中目标,进行全程机动飞行,设计飞行器在整个滑翔飞行过程中进行蛇形机动,使弹道不规则,加大对方反导系统的拦截难度.将倾侧角σ用N段常值函数进行离散,离散后每段的持续时间相等.其中,N是正整数,根据轨迹横向机动的次数来确定,本文取N=10.优化变量选取每一段的倾侧角大小及总的飞行时间.结果如图8和图9所示,图中,R为纵程,X为横程.
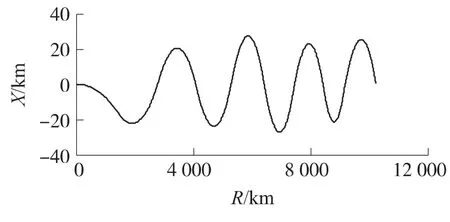
图8 横向蛇形机动轨迹地面投影

图9 横向蛇形机动控制变量
5.2 纵向机动方式
下面给出的2种机动方式均位于纵平面内,飞行过程中倾侧角为0°.
5.2.1 滑翔跳跃机动
针对2.7中介绍的第2类可避让禁飞区,可以规划一种更简单的避让机动方式.先让飞行器按拟平衡滑翔飞行,当接近目标时通过一次跳跃,躲过目标防御系统.拟平衡滑翔阶段只进行弹道积分,不进行优化计算.当接近目标时,对攻角进行离散处理,方法与横向机动倾侧角的离散方式相似,然后将离散后的分段攻角幅值和持续时间作为优化变量,求解非线性规划问题.
图10为滑翔跳跃机动飞行轨迹,假设飞行器从(0°,0°)开始滑翔,禁飞区是位于(100°,0°)处半径45km的半球,图中用虚线表示;目标位于赤道面上禁飞区之后.图10(b)为图10(a)的局部放大图.以纵程最大作为目标函数,进行弹道设计.
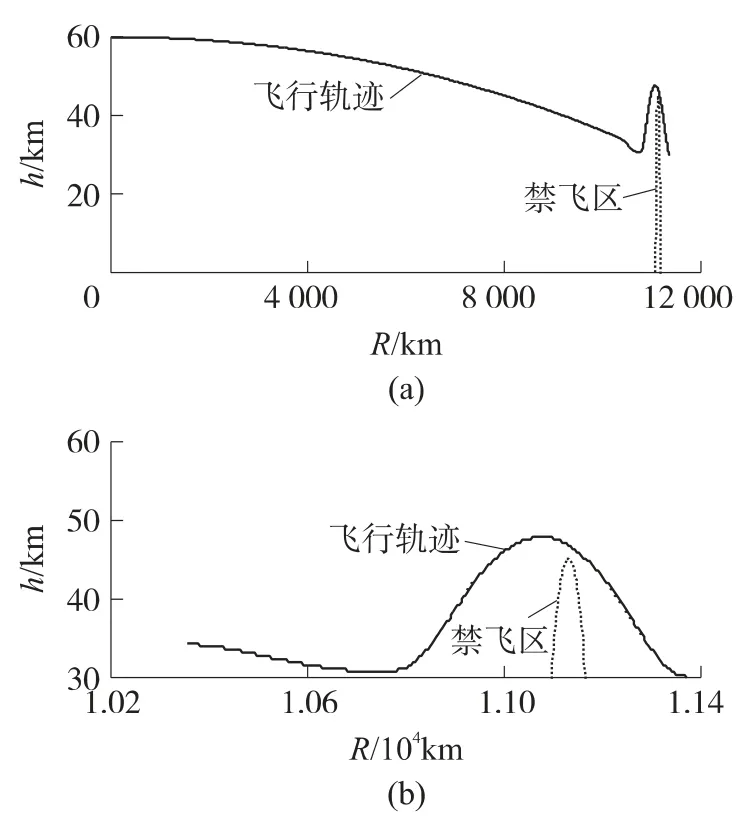
图10 滑翔跳跃机动飞行轨迹
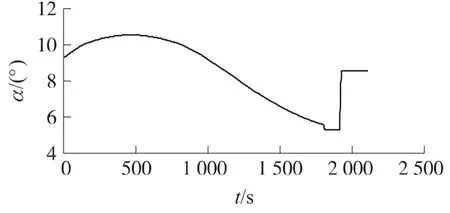
图11 滑翔跳跃机动攻角
5.2.2 纵向蛇形机动
面对横向机动方式5.1.3中的目标情况,还可以通过纵向全程跳跃机动,加大防御系统的拦截难度.有别于最大升阻比跳跃弹道,此处对弹道倾角进行了约束,最大幅值不超过1°,避免飞行器因跳跃幅度过大而失控.以拟平衡滑翔飞行弹道的攻角规律作为离散后攻角的初值,可以保证优化出的弹道在拟平衡滑翔弹道附近做小幅振动,既便于工程实现,又能达到机动突防的效果.
此处,给定目标位置(104°,0°),以飞行时间最短作为目标函数,得到机动弹道如图12~图14所示.

图12 纵向蛇形机动飞行轨迹

图13 纵向蛇形机动攻角

图14 纵向蛇形机动飞行走廊
6 结论
根据航路点、禁飞区和目标的分布情况,本文设计了5种机动突防模式弹道.其中,前3种属于横向机动方式,设计倾侧角的变化规律,攻角可通过拟平衡滑翔条件得到.后2种属于纵向机动方式,设计攻角规律,倾侧角恒为0°.设计出的5种机动弹道的攻角规律、倾侧角规律都比较简单,而且得到的弹道满足各种约束要求,验证了本文设计方法的有效性.
[1]SHINAR J,STEINBERGT D.Analysis of optimal evasive maneuvers based on a linearized two-dimensional kinematic model[J].Journal of Aircraft,1977,14(8):795-802.
[2]TROTTEMANT E J,SCHERER C W.Robust minimax strategies for missile guidance design[C].AIAA Guidance,Navigation and Control Conference and Exhibit.Honolulu,Hawaii:AIAA,2008.
[3]MAURO P,BRUCE A C.Optimal interception of evasive missile warheads:numerical solution of the differential game[J].Journal of Guidance Control and Dynamics,2008,31(4):1 111-1 123.
[4]JORRIS T R,COBB R G.2-D trajectory optimization satisfying waypoints and no-fly zone constraints[J].Journal of Guidance,Control,and Dynamics,2008,31(3):551-572.
[5]JORRIS T R,COBB R G.Three-dimensional trajectory optimization satisfying waypoints and no-fly zone constraints[J].Journal of Guidance,Control,and Dynamics,2009,32(2):543-553.
[6]赵汉元.飞行器再入动力学和制导[M].长沙:国防科技大学出版社,1997.ZHAO Han-yuan.Vehicle reentry dynamics and guidance[M].Changsha:National University of Defense Technology Press,1997.(in Chinese)
[7]ZHANG K,CHEN W.Trajectory optimization for hypersonic vehicle satisfying maneuvering penetration[J].Applied Mechanics and Materials,2011,110:5 223-5 231.
[8]SHEN Z,LU P.On-board generation of three-dimensional constrained entry trajectories[J].Journal of Guidance,Control,and Dynamics,2003,26(1):111-121.
[9]PHILIPS T H.A common aero vehicle(CAV)model,description,and employment guide[EB/OL].[2003].http://www.dtic.millmatris/sbir041/srch/af031a.doc.
[10]BETTS J T.Practical methods for optimal control using nonlinear programming[M].Washington:Society for Industrial and Applied Mathematics,2001.

