关于“混沌理论”的教学研究

殷 春 英

(衡水学院 电子信息工程学院，河北 衡水 053000)

关于“混沌理论”的教学研究

殷 春 英

(衡水学院 电子信息工程学院，河北 衡水 053000)

混沌理论已经涉及到了社会科学、自然科学的各个领域，对混沌理论的理解显得尤为重要，探究对混沌理论的教学方法摆在了每一位基础理论工作者的面前，实践证明，采用对比分析、结合实例和图形的方法能产生较好的教学效果．

混沌理论；内在随机性；初值敏感性；倍周期分岔

“混沌理论”是继相对论、量子力学之后发展起来的又一新兴的交叉学科．实践证明，混沌现象无处不有，“混沌理论”几乎遍及了各个领域，随着计算机技术的发展，对“混沌理论”的研究也更加深入，如何正确理解“混沌理论”也直接影响到学生对实际问题的处理．本文就是探究“混沌理论”的教学方法，加深对“混沌理论”的理解，为后继课程的学习、问题的探究打下坚实的基础．

1 对比理解“混沌理论”所描绘的物理图景

谈到描述物体运动的物理景观，大家首先想到的是“牛顿力学”，即，告诉我们运动规律和初始条件，我们就可以用求导的方法预见未来物体的变化规律，反之，如果知道当今的变化规律和初始条件，我们就可以用积分的方法推算出以前物理的位置和状态．以“天体力学”为例，“天体力学”曾经是描述确定论的典范，蕴含着“一一对应”的关系，即当给定了一组确定的初值，就可以确定一条不变的运动轨道，由此就确定了此体系的过去和未来的变化规律，“牛顿力学”所描述的物理世界是一幅简单的、静态的、可逆的、永恒不变的自然景观，是关于“状态”的机械的自然观[1]．

而我们面临的真实的世界是复杂的，是一个动态的、不可逆的、随机变化着的自然景观，而“混沌理论”就是研究这种真实的物理世界，是一种关于过程的科学、演化的科学、动态的科学，即演化的自然观．

2 突出“混沌理论”的特点

“混沌理论”不同于机械的自然观，它描述的是一个复杂的、动态变化的自然界，所以，它要有自己的独特性．

2.1 内随机性

随机性是指在一定的条件下，系统的某种状态可能出现、也可能不出现．随机性又分为内随机性和外随机性．如果系统的随机性由系统的外部作用引起的，我们称这种随机性为外随机性；如果系统的随机性由系统的内部作用引起的，我们称这种随机性为内部随机性．按牛顿力学的观点来分析，一个确定性系统在不受外来干扰时，它自身是不会出现随机性的，即只存在外随机性．随着现代科学技术的发展，人们发现，许许多多不受外部干扰的确定系统也存在随机性的现象，即完全确定性的系统在不受外来干扰时出现的随机性为内随机性．也就是说，真实的物理世界不仅存在着外随机性也存在着内随机性，而内随机性正是混沌的一大特征，它反映的是一个复杂的、动态的、真实的物理世界．

2.2 初值的敏感性

经典力学认为，只要研究对象的初始条件给定(同时边界条件也给定)，经过运算可以求出方程的解，即研究对象随后每时每刻的状态也就随之确定，我们称这种系统为确定性的系统，换言之，由确定性系统所描述的物体的运动紧密地依赖于所给的初始条件．这就是常言的动力学系统的稳定性，它是一般动力系统中一个非常重要的概念．这里的稳定性是指系统受到微小扰动保持原有状态的属性或能力．

而“混沌理论”有所不同，如同人们所说的“天有不测风云”，就是指气候系统对初始条件非常敏感，形象地来比喻就是“蝴蝶效应”：因为几千公里以外一只蝴蝶翅膀的小小扇动，就有可能使得气象学家无法预测几星期之后的天气情况，即产生不确定性．这种初值的微小差别将导致最终输出的巨大差别的性质就是初值的敏感性．

2.3 混沌运动只能出现在非线性系统中

我们在以前只是涉及到线性系统即线性微分方程，也就是牛顿力学，只要给定了初始条件，解就确定了，不会出现混沌运动．

混沌的出现是由于系统有不同的流域和不止一个定点，在系统的条件适当时，它会在这些不同的流域之间来回地跳动，只有这样才可能出现混沌，而这种在不同流域或几个定点只能在非线性系统中才能出现．所以说，只有在非线性系统才可能出现混沌．

3 了解通向“混沌”的具体通道

前面已提到，混沌运动只能在非线性系统中才可能出现，而非线性是自然界中普遍存在的现象，所以科学家们认为“条条道路通混沌”，具体地说，至今为止，人们所了解的通向“混沌”的道路有：准周期过程、茹厄勒-塔肯斯道路、倍周期分岔、阵发混沌等，下面以倍周期分岔进入混沌为例，认识一下通向混沌的通道．

众所周知，系统运动变化的有序状态常常体现于它的周期性，但是，随着条件的变化，系统的周期性就会发生变化，进行倍周期分岔，随着分岔点的增多，系统就会丧失原来的周期性，而进入混沌状态．

下面以受迫达芬方程为例来研究系统是如何由稳态进入混沌的[2]：

设：α=0.3,k=-1,μ=1则能求得此方程在相平面上的3个定点S、F1、F2，其中S是不稳定的，另2个是稳定的．计算机计算表明，初时条件不在阴影区的轨线最终都趋于右侧的F2，初时条件在阴影区的轨线最终都趋于F1．这样，整个的相空间就依赖定点被分成了不同的流域，不同流域的轨线将趋于不同的稳定点，到底趋于哪一点，由初始条件决定．如图1．

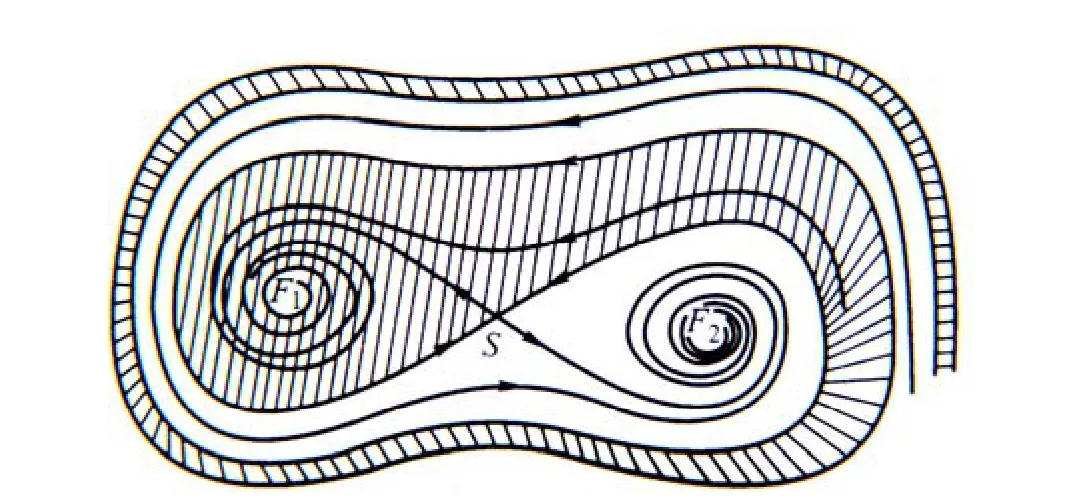
图1 达芬方程的定点和不同流域

将F继续增大，系统绕焦点的振荡出现分频，即倍周期τ=2T，如图 2(b)所示，它所对应的相图轨迹如图3(b)所示．

再继续增大F，振荡周期依次成倍变化，即τ=2nT，n是正整数．

在继续增大F，当超过某一临界值时，系统将从原来的流域跳到另一个流域，在另一焦点附近振荡．同样，这种振荡也可能又跳回到原来的流域，在原来焦点附近振荡．系统内部的微小变化或轻微的噪声都会使系统从一个流域进入另一个流域，而且很难再按原来的轨道运动，出现了随机性，我们把这样的运动称为混沌，如图2(e-i)所示，它所对应的相图轨迹如图3(e)所示．

由此可见，当受迫达芬方程中的F不断增大时，系统的振荡周期由T变为 2T，随机变为 22T，……，2nT，直至出现混沌，所以说，倍周期分岔是通向混沌的一条通道．

总之，对于“混沌理论”的教学，笔者采用的是从宏观到具体，从具体到实例，通过计算机绘图的讲解方法，符合学生的认识规律，更有利于学生对知识的掌握．

图2 达芬方程中F取不同值时的x-t曲线

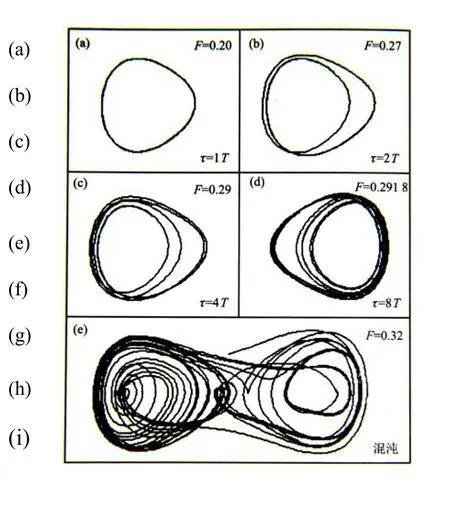
图3 相平面上的轨迹

[1] 黄润生,黄浩.混沌及其应用[M].2版.武汉:武汉大学出版社,2005:15-17.

[2] 刘秉正.非线性动力学[M].北京:高等教育出版社,2007:132-136.

On the Teaching of “Chaos Theory”

YIN Chun-ying
(College of Electronic and Information Engineering, Hengshui University, Hengshui, Hebei 053000, China)

Since chaos theory has involved every field of social science and natural science, the understanding of it appears especially important, and the exploration of the teaching method of chaos theory should be the work for every basic theoretical worker. Practice proves that adopting the methods of contrastive analysis and the combination of examples with graphs can have a better teaching effect.

chaos theory; inherent randomness; initial value sensitivity; period-doubling bifurcation

G642

A

1673-2065(2012)01-0102-03

2011-07-20

河北省教育科学研究“十一五”规划课题(08020005)

殷春英(1966-),女,河北冀州人,衡水学院电子信息工程学院教授.

(责任编校：李建明英文校对：吴秀兰)