磁保持继电器短耐试验通电时间的波动问题研究

曾作钦，郑立新，郑美海

（福建省产品质量检验研究院，福建 福州 350002）

1 引言

低压配电线路发生短路故障时，线路总阻抗的减小，会导致短路电流超出该线路额定电流的许多倍，如大容量低压配电系统，可达几万到几十万安培。短路故障电流通过电器时，会同时产生电动力效应和热效应，并同时对电器起作用，而且这两种效应对电器的破坏作用又是相互关联的。电动力效应在电器的动、静触头间所产生的斥力可使触头的接触电阻增大、发热量增加，即热效应增加，从而使电器所有载流部件的机械强度下降，降低了耐受电动力的能力。短路电流产生的巨大电动力效应和热效应会使导体变形、绝缘破坏、短路电路中的电气元件损坏[1-2]。

因此，安装在线路上的电器在发生短路故障的短暂时间内应该能经受住短路电流的冲击，不受破坏。额定短时耐受电流能力试验(以下简称短耐试验)[1]，就是用于考核开关电器在发生过载和短路故障的情况下，不分断电路但能承受短时间、大电流所形成的电动力和热效应的作用而不致于破坏的能力，是对电器电动稳定性和热稳定性的一种综合考核。在试验过程中，电器只需承载试验电流，不接通也不分断此试验电流，而这些操作是人为地借助一定手段来实现的。

2 短耐试验通电时间的波动问题

本所拥有的50kA和10kA通断实验系统分别可用于电流小于50kA和10kA开关电器的接通与分断、短耐等试验。长期以来，两个试验系统都有进行定期的检修、维护和计量，运行状态一直都很稳定。然而，在某次完成某企业委托的较大批量磁保持继电器的短耐试验过程中发现，即使系统中预先设定的短耐通电时间保持不变，试验后测得的实际时间值都表现为较大范围的无规律波动。图1所示为10个相同系列规格的磁保持继电器在50kA系统中进行耐受电流为12kA的短耐试验后实测通电时间数据，试验要求它们经受该电流冲击的时间不少于66.6ms。从图中可以看到，10次试验的时间大概在72ms～79ms之间波动，看似结果挺满意，但计算可知，该波动范围超过总试验要求时间的10%，并且这些数据似乎杂乱无章，容易对该产品性能的分析和评价产生一定的影响。那么，导致通电时间出现这样混乱的原因何在，是否这些时间数据真的是毫无规律可循？后续文章将就这些问题展开详细的分析和讨论。

图1 12kA短耐试验的时间数据分布图

3 正交多项式曲线拟合及其应用

3.1 正交多项式曲线拟合

在科学实验和统计分析研究中，常常需从一组实验数据(xi，yi)(i=1，2，3，…，n)出发，寻找自变量x和因变量y之间的关系，也就是通过离散数据建立数学模型，从中获得变量相互间的变化关系。由于实验数据往往有不准确性，因此，只要求曲线按一定标准符合离散点分布的总体特征，而不要求它精确地通过所有的离散点，这就是所谓的“曲线拟合”。正交多项式曲线拟合是一种精度比较高的曲线拟合方法，并且它能有效避免最小二乘拟合法中出现的病态方程问题，因此，在各个科学领域中得到了广泛的应用[3-4]。下面给出关于正交多项式曲线拟合的具体定义[5]。

对给定数据（xi，yi）（i=1, 2, 3, …,），设采用以下正交多项式来拟合：

3.2 基于正交拟合的短耐时间波动分析

下面将借助这种正交多项式曲线拟合的方法对第二节中提出的问题进行分析和研究。根据3.1中的定义和分析可知，1次正交多项式拟合曲线就是一条直线，而2次正交多项式拟合曲线是熟悉的抛物线曲线，显然，它们是无法满足图1所示数据的分布特征。

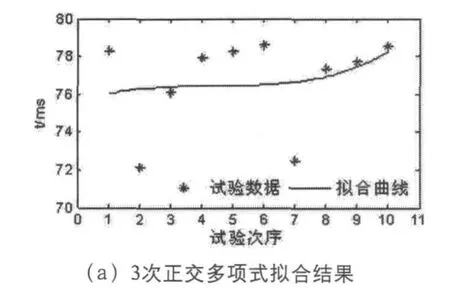
图2 正交多项式的拟合结果

为此，我们从3次正交多项式开始对图1中的数据点进行拟合，得到的3～6次正交多项式的曲线拟合结果，分别如图2(a)～2(d)所示。从图2(a)中能看到，3次正交拟合曲线与数据的分布情况相差甚远，完全不能满足需要；在图2(b)中可见，试验数据点大多零散地落于曲线的上方，与曲线上对应的数值点基本存在较大的误差，说明4次正交拟合曲线无法满足要求；而从图2(c)中可清楚地看到这些试验数据点基本落在曲线附近，与曲线上的对应值相差很小，除第7个试验数据可能是由于某些因素引起较大偏差，但其它数据点的拟合情况足以表明5次正交拟合曲线可以很好地再现图1所示数据的分布特征；再看图2(d)，它与图2(c)没有明显的区别，这再次证明采用5次正交拟合曲线在此处进行拟合是可以满足要求的，如果强制采用更高次的正交多项式进行拟合，只会无谓地增加对多项式系数分析计算的机器时间。此处所得5次正交多项式的一般表达式为：

需要说明的是，得到这样的结果并非偶然，用5次正交多项式对13组不同数量、不同系列规格的磁保持继电器，在不同时期进行不同电流的短耐试验后所得数据进行拟合，都可得到类似的满意结果。表1所示为正交拟合后，各组试验数据与所拟合曲线对应数据点存在的误差统计情况。可以看到，除了第2组数据由于初次试验操作不当等因素引起的个别数据点偏差较多而导致的总体误差值较大外，其余各组数据的平均误差都小于1ms，处于较稳定的状态，而对应的最大和最小误差也基本在较小的范围内波动，因此，在曲线拟合图中自然也能较好地反映出数据的分布特征。

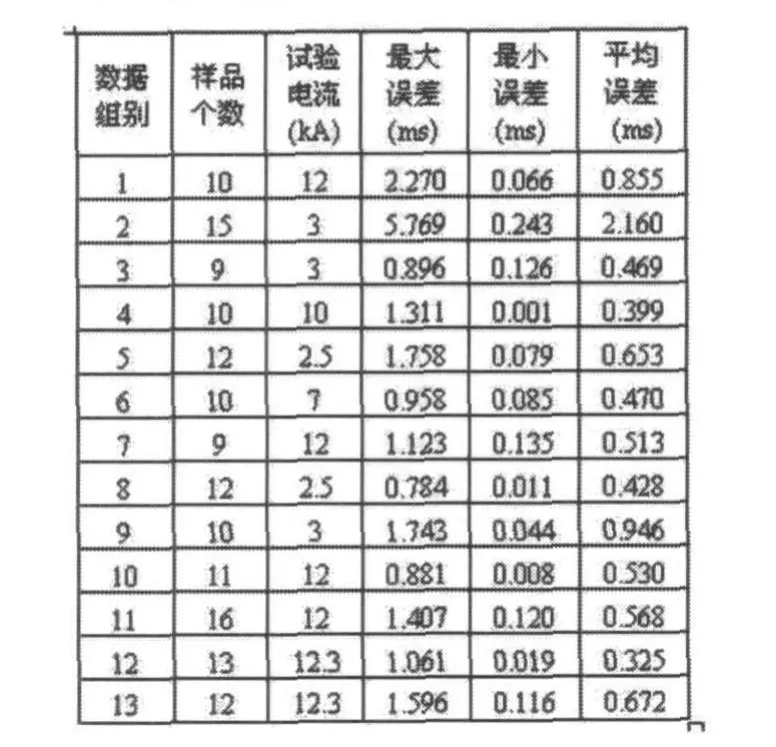
表1 各组试验数据的正交拟合情况

前面图2所研究的为表1中的第1组数据的拟合情况，结合前面的分析结果和曲线拟合的定义，可知所得结果是较满意的。下面不妨再来看表1中误差值较大的第2组试验数据及其用5次正交多项式的拟合结果，如图3所示。从图中可以看到，曲线上对应数值点与试验数据的拟合情况与表1中所分析误差情况是一致的，数据点基本都与曲线很贴近，却不与曲线完全重合，且个别数据点偏差较大，但是总体上还是能较好地反映出试验数据的特性，所得5次正交多项式的一般表达式为：

图3 第2组试验数据及其拟合结果

对比式(3)和式(4)，可以发现这两个5次多项式，无论是在数量级别还是在每一项的符号上，都表现出惊人的一致性。可见，这些试验数据并非毫无规律可循，它们很好地与5次多项式曲线的走势同步。这里从无规律到有规律的研究分析，对该产品相关性能的研究和质量好坏的判断，有着重要的作用。此外，我们知道，这两个多项式是对两组不同系列磁保持继电器在不同的短耐电流(这里采用了不同的实验系统)、不同通电时间下试验数据的拟合结果，为什么会如此的相似呢？

分析这两个实验系统的线路原理图发现，它们有一个共同之处，就是系统中通常被设置用于分断和保护试验电路安全的开关电器是同一企业生产的同一型号万能式断路器，只是各自的额定电流不同。那么，造成短耐试验时间值出现这种规律变化的原因很可能就是，断路器的分励脱扣器或实现分断机构的性能也是符合这种规律变化所引起的，这将在后续工作中进行专门的研究，并另文进行探讨。

4 结论

额定短时耐受电流能力试验用于考核电路上的电器在发生短路故障的短暂时间内经受短路电流冲击的能力。文中借助正交多项式拟合方法对磁保持继电器短时耐受试验时间数据出现的波动现象进行研究，通过对多组数据拟合误差的深入分析，发现5次正交多项式能有效地拟合出不同系列产品在不同试验电流下的短耐试验结果的特征，并且多项式各项的系数级别和符号都基本一致，有效地揭示了这些数据中隐含的规律。最后，根据所发现的分布规律分析了可能导致这种现象的原因。

[1]陆俭国，张乃宽，李奎.低压电器的试验与检测[M].北京：中国电力出版社，2007：124-134.

[2]冯璟，季慧玉.提高断路器短时耐受电流性能的研究和分析[J].低压电器，2011，33（10）：1-5.

[3]朱晓东，鲁铁定, 陈西江.正交多项式曲线拟合[J].华东理工大学学报：自然科学版，2010，33（4）：398-400.

[4]薛林，刘琚，辛化梅等.基于正交多项式拟合的非视距定位优化算法[J].山东大学学报：工学版，2010，40（6）：12-16.

[5]郑咸义，雷秀仁，陆子强.应用数值分析[M].广州：华南理工大学出版社，2008：90-123.