扰动重力梯度张量单分量和组合分量最小二乘配置法模型的建立
刘晓刚,吴晓平,王 凯
1 信息工程大学测绘学院,郑州 450052
2 西安测绘研究所,西安 710054
扰动重力梯度张量单分量和组合分量最小二乘配置法模型的建立
刘晓刚1,2,吴晓平1,王 凯1
1 信息工程大学测绘学院,郑州 450052
2 西安测绘研究所,西安 710054
建立了利用扰动重力梯度张量Tzz分量和Txx+Tyy、Tzz-Txx-Tyy组合分量确定地球重力场的调和分析法模型,进一步推导了扰动重力梯度张量对角线三分量的自协方差和互协方差函数的级数展开式,推导了单分量、组合分量与重力位系数之间协方差函数的实用计算公式,给出了利用单分量和组合分量解算地球重力场模型的最小二乘配置法基本原理公式.结果表明,最小二乘配置法具有一定的抗差能力,随着观测数据误差的不断增大,其恢复的重力场模型有效阶次不断降低,精度也不断下降;Tzz-Txx-Tyy组合分量解算重力场模型的精度最高,其次为Tzz分量,Txx+Tyy组合分量最差.
地球重力场模型,调和分析法,最小二乘配置法,卫星重力梯度,GOCE
1 引 言
最小二乘配置法(LSC:Least Squares Collocation)是近代地球重力场逼近中非常重要的一项研究成果.特别是随着GOCE卫星测量计划的提出和实施,该方法作为确定全球或局部区域地球重力场模型的方法之一也备受关注,其理论也得到了进一步的发展和完善.
Schwarz和Krynski[1]研究了联合卫星重力梯度(SGG:Satellite Gravity Gradient)数据和陆地重力测量数据精化局部大地水准面的LSC方法;Tscherning[2]研究了最小二乘法和配置法在从空间测量数据中提取重力场信息以及将其与地面重力测量数据进行融合中的应用,并指出两种方法在观测量和参数个数相等时是等价的;罗志才[3]提出的频域LSC法可以有效提高计算速度;Li和Sideris[4]联合采用卫星测高获取大地水准面高数据和船测重力异常数据,对LSC法、频域最小二乘法以及多输入/单输出系统理论恢复局部地球重力场的精度进行了比较;张传定[5]完善了LSC理论,提出了最小二乘复配置理论,得到了各类单定边值问题的解析解、调和分析解、最小二乘解和最小二乘复配置解,建立了超定边值问题的最小方差解、最小二乘解和最小二乘复配置解;Tscherning[6]研究了利用LSC法估计全球重力场位系数及其误差估计的方法;Tscherning等[7]对仅采用扰动引力数据时由FFT(Fast Fourier Transform)方法确定的局部大地水准面,与联合扰动引力和GPS/水准数据由LSC方法确定的局部大地水准面精度进行了比较;Sansò和Tscherning[8]提出了快速球谐配置法,采用LSC法联合Tzz数据和地面重力异常数据进行了模拟试算;李迎春[9]利用引力位的协方差函数导出了位系数与引力位二阶导数的协方差函数模型,并推导出LSC法的实用解算公式;张嗥、陈琼[10]通过空间扰动位协方差函数特性,得出SGG数据与扰动位系数的相关协方差函数,利用LSC法,推导出由SGG数据直接解算引力位系数的函数表达式;汪海洪等[11]对不同分辨率的数据融合问题进行了初步研究,详细阐述了多分辩率LSC法的基本原理,推导了该方法的具体公式;Kotsakis[12]研究了在尽量不改变精度的前提下,通过消除LSC法内在的平滑效应来增强其恢复地球重力场能力的方法;章传银等[13]在分析局部重力场LSC法技术特点的基础上,推导出一种能综合多种类型、不同高度重力场元经验协方差函数的通用表达方法;吴星等[14]推导了扰动引力梯度数据与球谐系数之间的协方差阵和自协方差阵,并有效利用FFT技术将其降阶,得到了引力梯度径向分量LSC法的完整计算公式.
本文首先建立了利用扰动重力梯度张量Tzz分量和Txx+Tyy、Tzz-Txx-Tyy组合分量解算地球重力场的调和分析法模型,进一步推导了扰动重力梯度张量对角线三分量之间的自协方差和互协方差函数的级数展开式,推导了单分量、组合分量与重力位系数之间协方差函数的计算公式,给出了利用单分量和组合分量解算地球重力场模型的LSC法基本原理公式,最后对本文建立的LSC法模型进行了数值实验验证.
2 单分量和组合分量的调和分析法模型

扰动重力梯度张量对角线三分量的地心球坐标表达式为[15]其中,fM为引力常数;r为卫星轨道上任意一点的地心向径;θ和λ分别为它的地心余纬和地心经度;R为地球平均半径为完全正常化地球扰动引力位系数;n和m分别为球谐系数的阶和次;nm(cosθ)为完全正常化缔合勒让德函数.
将(2)式和(3)式相加,可以得到Txx+Tyy组合分量的表达式:
利用(1)式减去(4)式,可以得到Tzz-Txx-Tyy组合分量的表达式:

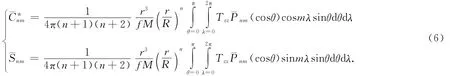
同理,可得利用Txx+Tyy、Tzz-Txx-Tyy组合分量解算位系数和的调和分析法公式分别为
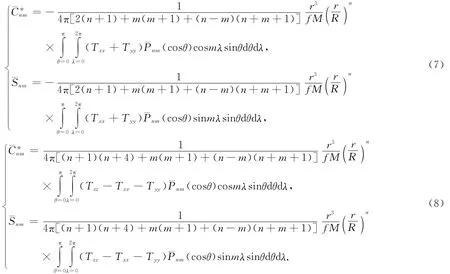
上述Tzz分量以及Txx+Tyy、Tzz-Txx-Tyy组合分量的调和分析法模型采用的都是格网中点值,如果采用格网平均值,则需要加入平滑因子,关于平滑因子的计算,请参阅文献[17].
3 单分量和组合分量的最小二乘配置法模型
在研究地球重力场的有关问题时,扰动位的协方差是最基本的,其它重力场元(重力异常、高程异常、垂线偏差和重力梯度张量等)之间的协方差都可以由它求得.空间扰动位协方差函数的级数展开式为[5,18]
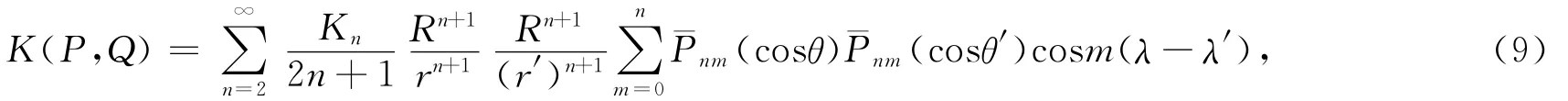
其中

式中Kn在一定阶次N以内的值,通常是利用参考重力场模型系数来计算,高于N以上阶次的值一般利用重力异常的阶方差模型求得,其关系为

如果采用Moritz提出的两分量模型,其形式为[19]

其中,α1,α2,S1,S2为实常数;A,B为整常数.取

α1,α2的单位是(mGal)2,其它量是无量纲的数.(Δg)不能由(12)式计算,一般采用(Δg)=7.5(mGal)2.
根据扰动重力梯度张量对角线三分量与扰动位T之间的关系式(1)—(3),并考虑到扰动位协方差函数的级数展开式(9),可以推导出扰动重力梯度张量对角线三分量的自协方差和互协方差函数级数展开式为


由扰动重力梯度张量Tzz分量解算位系数的调和分析法公式(6),考虑到Tzz分量的协方差函数级数展开式(14),调换求和与积分次序,并根据球谐函数的正交性,可以得到Tzz分量与位系数的协方差公式为

根据Txx+Tyy组合分量解算位系数的调和分析法模型(7)式,考虑到Txx和Tyy分量的自协方差以及互协方差函数级数展开式(15)、(16)、(19),调换求和与积分次序,并根据球谐函数的正交性,可以得到Txx+Tyy组合分量与位系数的协方差公式为

根据Tzz-Txx-Tyy组合分量解算位系数的调和分析法模型(8)式,考虑到Txx、Tyy和Tzz分量的自协方差以及互协方差函数级数展开式(14)—(19),调换求和与积分次序,并根据球谐函数的正交性,可以得到Tzz-Txx-Tyy组合分量与位系数的协方差公式为

下面给出利用扰动重力梯度张量Tzz分量以及Txx+Tyy、Tzz-Txx-Tyy组合分量解算地球重力场模型的LSC法的基本原理公式[3,5,9,14]:

式中,J表示位系数的列向量.其它几个量表述如下:
(1)单分量Tzz
对于单分量Tzz,则(23)式中表示位系数与Tzz分量的协方差矩阵,由(20)式进行计算;表示Tzz分量之间的协方差矩阵,由(14)式进行计算;Tij表示全球规则平均扰动重力梯度张量Tzz分量形成的列向量.
(2)组合分量Txx+Tyy
对于组合分量Txx+Tyy,则(23)式中表示位系数与Txx+Tyy组合分量的协方差矩阵,由(21)式进行计算;表示Txx+Tyy组合分量之间的协方差矩阵,由(15)、(16)、(19)式进行计算;Tij表示全球规则平均扰动重力梯度张量Txx+Tyy组合分量形成的列向量.
(3)组合分量Tzz-Txx-Tyy
对于组合分量Tzz-Txx-Tyy,则(23)式中表示位系数与Tzz-Txx-Tyy组合分量的协方差矩阵,由(22)式进行计算,而表示Tzz-Txx-Tyy组合分量之间的协方差矩阵,由(14)—(19)式进行计算;Tij表示全球规则平均扰动重力梯度张量Tzz-Txx-Tyy组合分量形成的列向量.
4 数值实验与结果分析
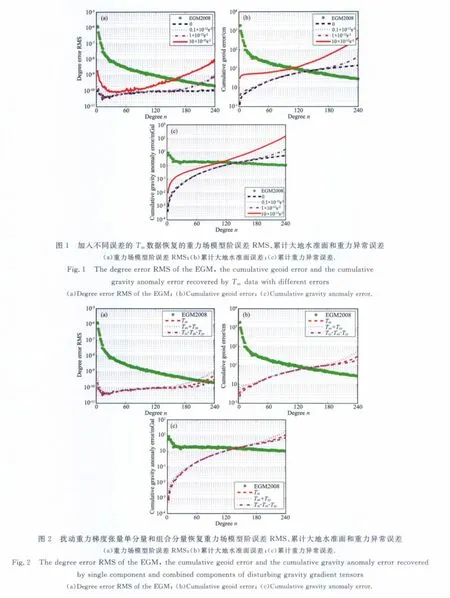
在具体数值实验中,首先利用EGM2008重力场模型生成了GOCE卫星轨道上的重力梯度数据[20],通过延拓[21]和格网化方法[22]将重力梯度数据归算为250km平均轨道高度处45′×45′的格网平均值,并对两极数据空白区进行填充,得到全球范围内的重力梯度格网平均值数据;向45′×45′的全球扰动重力梯度格网平均值数据中分别加入标准差为0、0.1、1×10-12s-2和10×10-12s-2的零均值白噪声,通过LSC法,采用FFT技术解算地球重力场模型,来测试不同的数据噪声对重力场模型解算结果的影响,其对应的重力场模型阶误差RMS、累计大地水准面和重力异常误差如图1所示,表1表示加入不同误差的Tzz数据恢复120阶重力场模型对应的精度统计结果.
其次,利用含有0.5×10-12s-2零均值白噪声的45′×45′全球扰动重力梯度格网平均值数据,对本文推导出的单分量Tzz和组合分量Txx+Tyy、Tzz-Txx-Tyy的LSC法模型的有效性进行测试,其对应的重力场模型阶误差RMS、累计大地水准面和重力异常误差如图2所示,表2表示单分量Tzz和组合分量Txx+Tyy、Tzz-Txx-Tyy数据恢复120阶重力场模型对应的精度统计结果.
从图1和表1可以看出,当观测数据含有不同的误差时对解算结果的精度影响较大,随着加入误差的不断增大,其恢复的重力场模型有效阶次不断降低,精度也不断下降.在Tzz数据中分别加入0.1×10-12s-2、1×10-12s-2和10×10-12s-2的零均值白噪声时,其恢复的重力场模型有效阶数分别约为140、135和110阶.含有10×10-12s-2误差的数据对最小二乘配置法解算结果的精度影响较大,而含有0.1×10-12s-2和1×10-12s-2误差的数据,其解算结果在2~240阶次内与不含误差的数据结果比较一致,这说明最小二乘配置法在解算含有误差的数据时具有一定的优势.其中,加入0.1×10-12s-2的误差数据恢复的120阶重力场模型,其对应的累计大地水准面误差达到5.938cm、累计重力异常误差达到1.095mGal的精度.
从图2和表2可以看出,Tzz-Txx-Tyy组合分量解算结果的精度最高,其次为Tzz分量和Txx+Tyy组合分量,这是因为扰动重力梯度张量的对角线三分量中,Tzz分量数据的量级最大,精度也最高,Txx和Tyy分量次之,在模型解算时,Tzz-Txx-Tyy组合分量不仅顾及了对角线三分量Tzz、Txx、Tyy的整体影响,而且各分量之间求差也在一定程度上削弱了数据中所含噪声对解算结果的影响;Tzz分量的解算结果优于Txx+Tyy组合分量的原因是,在对角线三分量中,Tzz分量对模型解算的贡献最大,另外,Txx+Tyy的组合在一定程度上放大了数据中所含噪声对解算结果的影响.单分量Tzz和组合分量Txx+Tyy、Tzz-Txx-Tyy恢复的120阶重力场模型对应的累计大地水准面误差分别达到5.994cm、6.111cm、5.944cm,累计重力异常误差分别达到1.105mGal、1.127mGal、1.096mGal的精度.
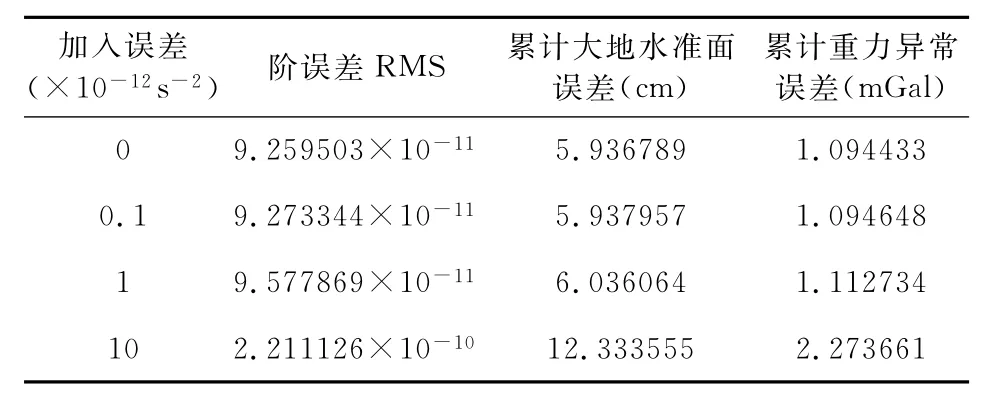
表1 加入不同误差的Tzz数据恢复120阶重力场模型的精度统计结果Table 1 The precision statistical results of the EGM in 120degree recovered by Tzzdata with different errors

表2 扰动重力梯度张量单分量和组合分量数据恢复120阶重力场模型的精度统计结果Table 2 The precision statistical results of the EGM in 120degree recovered by single component and combined components of disturbing gravity gradients
5 结 语
LSC法需要将重力梯度数据进行归算和格网化处理,得到平均轨道球面上的规则格网点或格网平均值数据,如果能预先确定格网的大小,则格网点的个数也就可以确定,从而法方程的维数也是一定的,并且由于该方法建立的法方程都是呈块状对角形式,因此方程的求逆等计算将非常简便、快捷;另外,该方法也可以综合各类观测数据确定地球重力场模型,在数据处理时能顾及观测量的误差,并且能够给出待估量的误差协方差信息.它的缺点是在将观测数据进行归算和格网化处理时,不可避免地引入了一些归算和格网化误差,并且要求有可靠的先验协方差模型,在恢复高阶次地球重力场模型时,需要解算超大型协方差矩阵的逆矩阵,由于大型矩阵求逆存在的病态性问题,从而影响了数值解的稳定性.
本文推导得到了利用扰动重力梯度张量Tzz分量以及Txx+Tyy、Tzz-Txx-Tyy组合分量解算地球重力场的最小二乘配置法模型,进一步充实了利用重力梯度数据解算地球重力场模型的方法,从而使得最小二乘配置法模型的内容更加丰富.
(References)
[1] Schwarz K P,Krynski J.Improvement of the geoid in local areas by satellite gradiometry.Bulletin Géodésique,1977,51:163-176.
[2] Tscherning C C.Collocation and least squares methods as a tool for handling gravity field dependent data obtained through space research techniques.Bulletin Géodésique,1978,52:199-212.
[3] 罗志才.利用卫星重力梯度数据确定地球重力场的理论与方法[博士论文].武汉:武汉测绘科技大学,1996.Luo Z C.Theories and method of the determination of the earth′s gravity field using satellite gravity gradients[Ph.D.thesis](in Chinese).Wuhan:Wuhan Technical University of Surveying and Mapping,1996.
[4] Li J,Sideris M G.Marine gravity and geoid determination by optimal combination of satellite altimetry and shipborne gravimetry data.Journal of Geodesy,1997,71:209-216.
[5] 张传定.卫星重力测量——基础、模型化方法与数据处理算法[博士论文].郑州:信息工程大学测绘学院,2000.Zhang C D.Satellite gravimetry:foundation,modeling methods,and data processing algorithms[Ph.D.thesis](in Chinese).Zhengzhou:Institute of Surveying and Mapping,2000.
[6] Tscherning C C.Computation of spherical harmonic coefficients and their error estimate using least-squares collocation.Journal of Geodesy,2001,75:12-18.
[7] Tscherning C C,Radwan A,Tealeb A A,et al.Local geoid determination combining gravity disturbances and GPS-levelling—a case study in the Lake Nasser area,Aswan,Egypt.Journal of Geodesy,2001,75:343-348.
[8] SansòF,Tscherning C C.Fast spherical collocation:theory and examples.Journal of Geodesy,2003,77:101-112.
[9] 李迎春.利用卫星重力梯度测量数据恢复地球重力场的理论与方法[硕士论文].郑州:信息工程大学测绘学院,2004.Li Y C.Theories and method of the recovery of the earth′s gravity field using satellite gravity gradients[Master′s thesis](in Chinese).Zhengzhou:Institute of Surveying and Mapping,2004.
[10] 张皞,陈琼.卫星重力梯度数据解算位系数的最小二乘配置法.测绘与空间地理信息,2005,28(6):34-35.Zhang H,Chen Q.Least squares collocation in calculating potential coefficient with satellite gravity gradiometry data.Geomatics and Spatial Information Technology(in Chinese),2005,28(6):34-35.
[11] 汪海洪,罗志才,罗佳,等.多分辨率最小二乘配置法初探.大地测量与地球动力学,2006,26(1):115-118.Wang H H,Luo Z C,Luo J,et al.Preliminary research on multi-resolution least-square collocation.Journal of Geodesy and Geodynamics(in Chinese),2006,26(1):115-118.
[12] Kotsakis C.Least-squares collocation with covariancematching constrains.Journal of Geodesy,2007,81:661-677.
[13] 章传银,丁剑,晁定波.局部重力场最小二乘配置通用表示技术.武汉大学学报(信息科学版),2007,32(5):431-434.Zhang C Y,Ding J,Chao D B.General expression of least squares collocation in local gravity field.Geomatics and Information Science of Wuhan University(in Chinese),2007,32(5):431-434.
[14] 吴星,张传定,刘晓刚.卫星重力径向梯度数据的最小二乘配置调和分析.测绘学报,2010,39(5):471-477.Wu X,Zhang C D,Liu X G.Least squares collocation harmonic analysis of the radial satellite gravity gradients.Geodaetica et Cartographica Sinica(in Chinese),2010,39(5):471-477.
[15] Reed G B.Application of Kinematical Geodesy for Determining the Short Wave Length Components of the Gravity Field by Satellite Gradiometry.Ohio State University,Dept.of Geod.Sciences,Rep.No.201,Columbus,Ohio,1973.
[16] 陆仲连.球谐函数.郑州:测绘学院出版社,1984.Lu Z L.Spherical Harmonic Functions(in Chinese).Zhengzhou:Institute of Surveying and Mapping Publishing House,1984.
[17] 陆仲连.地球重力场理论与方法.北京:解放军出版社,1996.Lu Z L.Theory and method of the earth′s gravity field(in Chinese).Beijing:PLA Publishing House,1996.
[18] 吴星.卫星重力梯度数据处理理论与方法[博士论文].郑州:信息工程大学测绘学院,2009.Wu X.Research of Methods of Spherical Harmonic Analysis of the Earth’s Gravity Field[Ph.D.thesis](in Chinese).Zhengzhou:Institute of Surveying and Mapping,2009.
[19] Moritz H.Advanced physical geodesy.England:Abacus Press,1980.
[20] 刘晓刚,吴晓平,赵东明,等.扰动重力梯度的非奇异表示.测绘学报,2010,39(5):450-457.Liu X G,Wu X P,Zhao D M,et al.Non-singular expression of the disturbing gravity gradients.Geodaetica et Cartographica Sinica(in Chinese),2010,39(5):450-457.
[21] 刘晓刚,李珊珊,吴星.卫星重力梯度数据的向下延拓.大地测量与地球动力学,2011,31(1):132-137.Liu X G,Li S S,Wu X.Downward continuation of the satellite gravity gradient data.Journal of Geodesy and Geodynamics(in Chinese),2011,31(1):132-137.
[22] 刘晓刚,吴晓平,王宝军,等.卫星重力梯度数据的网格化方法研究.大地测量与地球动力学,2010,30(6):60-65.Liu X G,Wu X P,Wang B J,et al.Study on gridding methods of the satellite gravity gradient data.Journal of Geodesy and Geodynamics(in Chinese),2010,30(6):60-65.
Construction of the least squares collocation models for single component and composite components of disturbed gravity gradients
LIU Xiao-Gang1,2,WU Xiao-Ping1,WANG Kai1
1 Institute of Surveying and Mapping,Information and Engineering University,Zhengzhou450052,China
2 Xi′an Research Institute of Surveying and Mapping,Xi′an 710054,China
This work constructs the spherical harmonic analysis models for single component Tzzand composite components Txx+Tyy,Tzz-Txx-Tyyof disturbed gravity gradients to compute earth′s gravitational field model(EGM).Besides,the series expansion formulae of variance and covariance functions of the diagonal components of disturbed gravity gradients are deduced.Then,the practical computational formulae of covariance functions between single component,composite components and the gravity potential coefficients are deduced.Finally,this work presents the fundamental formula of the least squares collocation(LSC)to compute EGM using the single component and composite components.The results show that the LSC is robust to a certain extent and the effective degree and precision of EGM decay gradually with the increase of errors.The precision of the EGM computed by the composite components Tzz-Txx-Tyyis the best,while that of the composite components Txx+Tyyis the least.
Earth′s gravitational field model(EGM),Spherical harmonic analysis method,Least squares collocation(LSC),Satellite gravity gradient(SGG),GOCE
10.6038/j.issn.0001-5733.2012.05.015
P223
2011-09-25,2012-05-10收修定稿
国家自然科学基金(41174026,41104047,41174017),中国科学院研究生院地球科学学院博士后基金(2010046),信息工程大学博士学位论文创优基金资助.
刘晓刚,男,1983年生,博士,助理研究员,主要从事卫星重力测量研究.E-mail:liuxiaogang_1949@163.com
刘晓刚,吴晓平,王凯.扰动重力梯度张量单分量和组合分量最小二乘配置法模型的建立.地球物理学报,2012,55(5):1572-1580,
10.6038/j.issn.0001-5733.2012.05.015.
Liu X G,Wu X P,Wang K.Construction of the least squares collocation models for single component and composite components of disturbed gravity gradients.Chinese J.Geophys.(in Chinese),2012,55(5):1572-1580,doi:10.6038/j.issn.0001-5733.2012.05.015.
(本文编辑 汪海英)

