PSO算法在物流配送车辆路径优化模型中的应用
青海大学管理科学与工程系 孙少龙
青海大学工商管理系 吴小涛
青海大学财经学院 张珂珂
青海大学管理科学与工程系 冯 凯 席小斌
1.引言
随着市场经济的发展和物流技术专业化水平的提高,物流配送业得到了迅猛发展。物流配送是指按用户的订货要求,在配送中心进行分货、配货,并将配好的货物及时送交收货人。在物流配送业务中,存在许多优化决策问题,通过制定合理的配送路径,快速而经济地将货物送达用户手中,配送路径的选择是否合理,对加快配送速度、提高服务质量、降低配送成本及增加经济效益都有较大影响。
2.物流配送车辆路径优化问题描述
物流配送路径优化问题可以描述为:从配送中心(或称物流据点)用多辆汽车向多个需求点(或称顾客)送货,每个需求点的位置和需求量一定,每辆汽车的载重量一定,要求合理安排汽车路线,使总运距最短,并满足以下条件:
(1)每条配送路径上各需求点的需求量之和不超过汽车载重量;
(2)每条配送路径的长度不超过汽车一次配送的最大行驶距离;
(3)每个需求点的需求必须满足,且只能由一辆汽车送货。本文建立的车辆路径问题的数学模型考虑了上述物流配路径优化问题的约束条件和优化目标。
设配送中心有K辆汽车,每辆汽车的载重量为Qk(k=1,2,…,K),其一次配送的最大行驶距离为Dk,需要向L个需求点送货,每个需求点的需求量为qi(i=1,2,…,L),需求点i到j的运距为dij,配送中心到各需求点的距离为d0j(i、j=1,2,…,L),再设nk为第k辆汽车配送的需求点数(nk=0表示未使用第k辆汽车),用集合Rk表示第k条路径,其中的元素 表示需求点 在路径k中的顺序为i(不包括配送中心),令rk0=0表示配送中心,则可建立如下物流配送路径优化问题的数学模型:
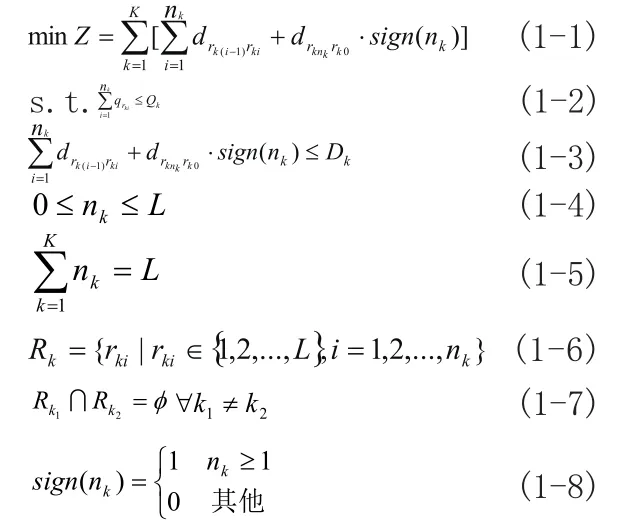
上述模型中:(1-1)式为目标函数,要求配送线路最短;
(1-2)式保证每条路径上各需求点的需求量之和不超过汽车的载重量;
(1-3)式保证每条配送路径的长度不超过汽车一次配送的最大行驶距离;
(1-4)式表明每条路径上的需求点数不超过总需求点数;
(1-5)式表明每个需求点都得到配送服务;
(1-6)式表示每条路径的需求点的组成;
(1-7)式限制每个需求点仅能由一辆汽车送货;
(1-8)式表示当第k辆汽车服务的客户数≥1时,说明该辆汽车参加了配送,则取sign(nk)=1,当第k辆汽车服务的客户数<1时,表示未使用该辆汽车,因此取sign(nk)=0。
3.粒子群算法描述
PSO算法将群体中的每个个体视为多维搜索空间中一个没有质量和体积的粒子(点),这些粒子在搜索空间中以一定的速度飞行,并根据粒子本身的飞行经验以及同伴的飞行经验对自己的飞行速度进行动态调整,PSO算法就是这样依据每个粒子对环境的适应度将个体逐步移到较优的区域,并最终搜索、寻找到问题的最优解。在PSO算法中,用粒子的位置表示待优化问题的解,每个粒子性能的优劣程度取决于待优化问题目标函数确定的适应值,每个粒子由一个速度矢量决定其飞行方向和速率大小。设在一个d维的目标搜索空间中,有m个粒子组成一个群体,其中,在第t次迭代时粒子i的位置表示为:Xi(t)=(xi1(t),xi2(t),xid(t)),相应的飞行速度表示为:Vi(t)=(vi2(t),vi2(t),vid(t))。开始执行PSO算法时,首先随机初始化m个粒子的位置和速度,然后通过迭代寻找最优解,在每一次迭代中,粒子通过跟踪两个极值来更新自己的速度和位置:一个极值是粒子本身迄今搜索到的最优解,称为个体极值,表示为Pi(t)=(pi1(t),pi2(t),pid(t));另一个极值是整个粒子群到目前为止找到的最优解,称为全局极值,表示Pg(t)=(pg1(t),pg2(t),pgd(t))。在第t+1次迭代计算时,粒子i根据下列规则来更新自己的速度和位置:

表1 各需求点周需求量(单位:吨)
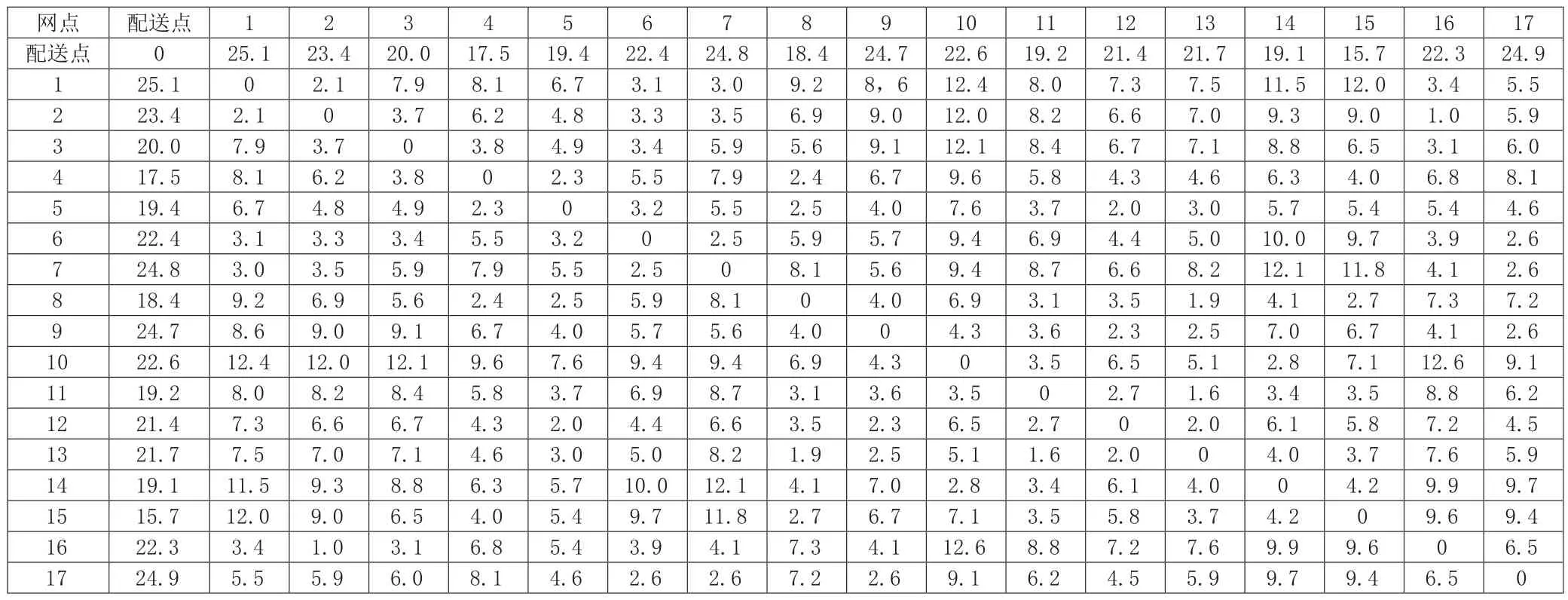
表2 需求点与配送中心及各需求点之间最短距离(单位:千米)

表3 最优值的迭代次数及所得到的最优解
Vib(t+l)=ωνib(t)+randl(pib(t)-xib(t))+rand2(pgk(t)-xik(t)) (2-1)
Xik(t+l)=xik(t)+νik(t+l) (2-2)
式中ω为惯性权重,ω取大值可使算法具有较强的全局搜索能力,ω取小值则算法倾向于局部搜索;rand1(pib(t)-xib(t))表示粒子对自身经验的依赖情rand2(pgk(t)-xik(t))表示粒子对社群信息的依赖情况。rand1,rand2表示0到1间的随机数。
4.举例具体演算分析
例如,设VRP问题中发货点任务数为7,车辆数为3,若某粒子的位置向量X为:
发货点任务号:1 2 3 4 5 6 7 8 9 X r:6 1 2 9 5 3 7 8 4 X v:6 1 2 0 5 3 7 0 4
利用Matlab求解该粒子对应解路径为:
车1:0→6→1→2→0
车2:0→5→3→7→0
车3:0→4→0
该表示方法的最大优点是使每个发货点都得到车辆的配送服务,并限制每个发货点的需求仅能由某一车辆来完成,使解的可行化过程计算大大减少。虽然该表示方法的维数较高,但由于PSO算法在多维寻优问题有着非常好的特性,维数的增加并未增加计算的复杂性。
5.华圣果业公司配送线路的分析与优化
5.1 华圣果业原配送线路基本数据分析
华圣果业公司主要给超市和农产品批发市场供应苹果。客户可分为需求量稳定的大客户和需求量随机的小客户。小客户的需求具有时间和地点上的不确定性,需求量小的特点,一般采用共同配送运输服务或客户自配卡车。大客户地点确定,主要位于西安市的超市或是农产品批发市场,但是经过实地的考察发现华圣果业公司现在主要只给西安市的各大超市供应苹果。大致共有20多个点,如人人乐、沃尔玛、华润万家、爱乐购超市等,公司为推广产品,采用每周专车送货上门服务。公司现拥有3辆半吨的长安货车和2辆1.5吨的东风小货车,若车辆使用欠缺时,可租赁车辆。
目前,华圣果业公司对大客户配送苹果并没有固定的配送线路,一般配送线路由货车司机自己来决定。更重要的问题是公司对于每个需求点会专门派一辆车去配送,不考虑是否满载率低的问题。这样的话就存在一些弊端:配送路线的选择不合理,运距过长,消耗作业时间偏多,不能充分利用车辆配载容积,浪费较多人力和物力资源,影响公司盈利。各需求点每星期需求苹果的基本数据如表1所示。
各编号对应的需求点名称如下:
1:华润万家西二环店
2:华润万家西安莲湖店
3:华润万家星火路店
4:人人乐超市北关购物广场
5:家乐福西安北大街店
6:人人乐购物广场西关店
7:大润发大唐西安店
8:爱乐购超市
9:西安沃尔玛万达店
10:沃尔玛购物广场西安金花南路分店11:人人乐东门店
12:沃尔玛购物广场西安骡马市分店13:人人乐解放路购物广场
14:华润万家金花路店
15:华润万家太华路店
16:百姓自选水果超市
17:家美家超市友谊路分店
5.2 基于PSO算法的物流配送路线优化
为计算方便,需考虑以下几个假设前提条件:
a、配送中心(华圣果业公司)不会出现缺货的可能并且对顾客的基本配送资料(需求量、地理位置)为已知,配送中心的位置也已知;
b、不考虑配送时间限制,即客户对货物的需求没有时间的规定;
c、不考虑每辆车为每个客户的服务时间,即不考虑每个客户的卸货时间;
d、车辆由配送中心出发,服务被指定的需求点后,再返回配送中心,区域内的需求点假设为固定数量且位置已知,不发生变动;
e、配送中心拥有一定数量的单一车型的配送车辆,且每辆车的容量已知。
f、每条配送路径上各客户需求量之和不超过配送车辆的容量;
g、每个客户只能由一辆配送车辆送货;
h、每辆车配送总里程不超过其最大行驶距离;
i、各道路均顺畅,不考虑交通堵塞拥挤等特殊情况。
在本题中,需要分别计算以下几个内容,计算需求点与配送中心及各需求点之间的距离,利用粒子群优化算法,求出函数的全局最优位置和最后得到的优化极值。
(1)问题重述
用0表示华圣果业有限公司(即配送中心),设车辆容量皆为q=8.0,公司有4辆车完成西安市内17家超市的配送任务,初始化群体个数n=30,惯性权重w=0.729,学习因子c1=2、c2=2,最大代数 MaxDT= 50。
(2)需求点与配送中心及各需求点之间的最短距离如表2。
(3)粒子群算法实现过程。
a、编码初始化
本文使用整数编码求解车辆路径问题。对于17个苹果需求点和4辆车来配送的问题,用从1到20的整数排列来表示粒子的状态X(x1,x2,…,xi),随机的生成初始种群,用1-20的整数是因为有4辆车来配送我们插入3个数就可将17个需求点划分成4组,然后由4辆车来分别给这4组需求点送货。编程的重点是要在每个粒子中找出这三个数用配送中心“0”来表示。
b、适应度计算
用PSO算法优化客户的排序,按照客户的排列顺序分配车辆,在每条线路的内部,用最邻近法优化线路。根据式(1-1)计算粒子所代表的配送方案的目标函数Z,粒子的适应度定义为目标函数Fitness=Z。
c、初始化局部最优和全局最优
d、循环内位置速度更新
微粒速度和位置的更新公式:
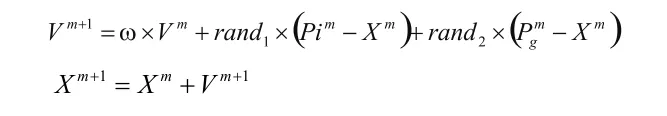
其中,Pi为微粒的自身最佳位置,Pg为群体的最佳位置。
①位置与速度的加法。粒子的位置更新时,若在速度矢量中 vi=0,则不改变位置中的第i个序列号;若 vi≠0,则交换粒子位置中的序号vi和xi,以保证新位置的有效性。
②位置间的减法。两个位置的相减结果是一个速度,记为 V= X2- X1。V按照以下方式来确定。逐一比较X1和X2的各个分量x1,i和x2,i,若两者相同,责令 vi=x2,i,否则令 vi=x1,i。
③速度的数乘。速度的数乘记为V2= w× V1,其中w为0到1之间的一个常数。速度的数乘按照如下方式执行:对于V1的每一维速度v1,i,随机生成一个0到1之间均匀分布的随机数rand,若rand≥c,责令v2,i= v1,i,否则令 v2,i=0。
e、循环内适应度计算
与初始适应度计算方法相同,根据式(1-1)计算粒子所代表的配送方案的目标函数Z。
f、循环内局部最优和全局最优更新
粒子的适应度计算完成后,每个粒子当前的适应度与自身己知的最优适应度比较,选出个体最优状态P;将种群中本次迭代的最优粒子适应度与种群已知的最优适应度比较,选择出群体最优状态Pg。交换更新全局最优和局部最优。
(4)算法得到的最优值的迭代次数及所得到的最优解,预计迭代次数50,共进行20次运算,如表3。
从实验结果分析,15次达到已知最优解,得到的最优总路径为:
0 →7 →6 →0 →1 →0 →2 →3 →4 →5 →0
对应的行车路线为:
车辆一:0 →7 →6 →0
车辆二:0→1→0
车辆三:0 →2 →3 →4 →5 →0
行车总距离217.81千米
6.结束语
由于PSO优化模型求解出来的结果是理想状态下的,因此需要结合华圣果业有限公司的实际情况进行有效地分析,才能更好地加以运用到实际情况中来。
[1]李丽,牛奔.粒子群优化算法[M].冶金工业出版社,2009.
[2]郎茂祥.配送车辆优化调度模型与计算[M].电子工业出版社,2009.
[3]李宁,邹彤,孙德宝.车辆路径问题的粒子群算法研究[J].系统工程学报,2004,19(6):597-600.
[4]吴建生,秦发金.基于MATLAB的粒子群优化算法程序设计[J].柳州师专学报,2005,20(4):97-100.

