成年食饵具有扩散的捕食系统周期解
刘艳伟
(周口师范学院数学系,河南周口466001)
近年来,非自治微分系统周期解的存在性、唯一性及全局稳定性被数学、生态学学者广泛研究[1-5]。大量的结论表明,周期解是非自治捕食系统的一个重要性质。获取周期解的存在性条件,对保护和控制处于周期波动环境中生物种群,具有重要的指导作用。
正如Xu等[2]所指出的,捕食-食饵系统中,种群的年龄结构及在异构环境中的扩散进程在一定条件下对系统的动力学有着复杂的影响。这也是许多作者关注的焦点[2,3]。在文献[1]的基础上,Xu等[2]构造了一类捕食种群具有年龄结构、食饵具有扩散的比率依赖型生物模型,并考虑了系统系数的周期性变化,得到了该系统存在周期解的充分条件。值得一提的是,Xu等[2]的模型没有考虑食饵的年龄结构,为此,本文改进Xu等的模型为如下形式:

并且系统(1)满足初值条件

其中x和y分别表示t时刻成年食饵种群在斑块i(i=1,2)的单位密度;z1和z2分别表示t时刻幼年捕食者和成年捕食者种群的单位密度;τi>0(i=1,2,3)为孕育期;Di>0(i=1,2)为扩散率函数;β1, β2,d1,d2,d3,v0,v1,D1,D2,m和αi(i=1,2,3)均为大于零的连续ω-周期函数,其相应的生物学解释可参见文献[2]。此外,考虑到初值的连续性,本文进一步要求

为简便起见,记fL=f(t),fM=(t),其中f(。)>0是连续的ω-周期函数。
1 周期解的存在性
为了获得系统(1)周期解存在的充分条件,需要一些优先的估计。
1.1 基本引理
引理1 设λ∈(0,1)为一参数,(u1(t),u2(t),u3(t))Τ是系统
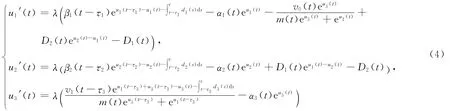
的ω-周期解。如果

成立,则|u1(t)|+|u2(t)|+|u3(t)|≤R1。

引理2 设μ∈[0,1]为一参数,(u1,u2,u3)Τ是方程组
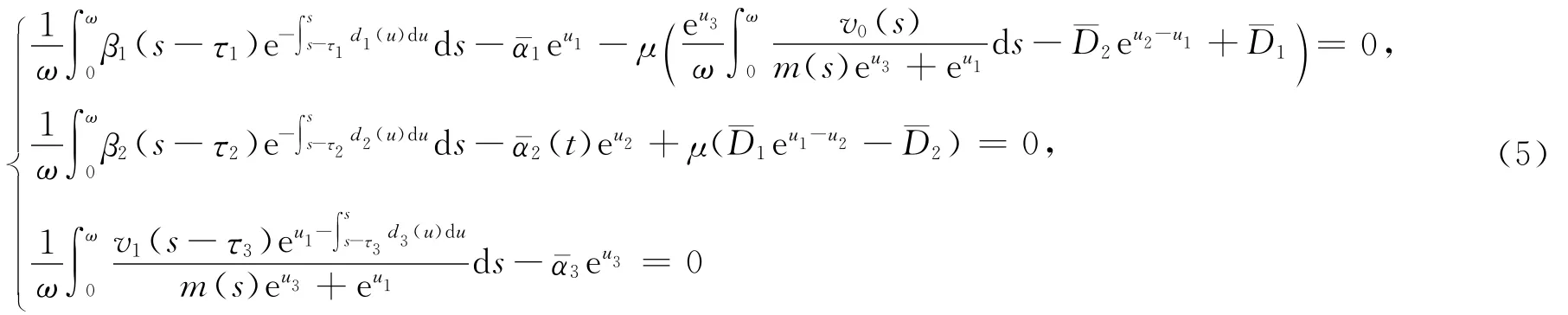
的解,则|u1|+|u2|+|u3|≤R2。

利用比较法,容易证明引理1、引理2成立。
1.2 主要结论
这里结合引理1、引理2的结论,并利用Gaines-Mawhin's重合度理论,获得了系统(1)周期解存在的充分条件。
定理1 设(H1)成立,则系统(1)在条件(2)、(3)下至少存在一个ω-周期解。
证 考虑系统(1)的子系统
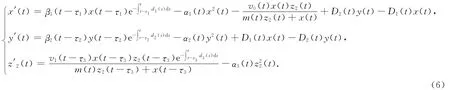
注意到系统(1)满足初始条件(2)的解是正的,所以可设

此时,系统(6)可变换为

显然,如果(u1(t),u2(t),u3(t))T是系统(8)的ω-周期解,则系统(6)具有一个形如(7)的ω-周期解。为了展示系统(8)存在ω-周期解,定义

其中X和Y是线性空间。定义一个Euclidean范数

则X和Y是此范数下的两个Banach空间。

和N:X→X,

在以上定义下,系统(8)满足Lu=Nu,u∈Dom L⊂X。

定义两个投影算子

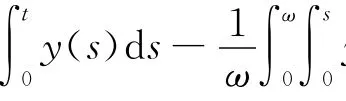

另一方面,QN和KP(I-Q)N是连续的,根据Arzela-Ascoli定理,QN和KP(I-Q)N在任何有界开集Ω⊂X是紧的,因此在¯Ε上对任何有界开集Ω⊂X,N是L-紧的。定义
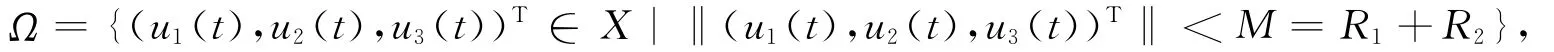
其中R1和R2由引理1和引理2定义。
当u=(u1(t),u2(t),u3(t))T∈∂Ω∩Dom L时,根据引理1得到Lu≠λNu,∀λ∈(0,1)。
当u=(u1(t),u2(t),u3(t))T∈∂Ω∩Ker L时,u∈R3且满足|u1|+|u2|+|u3|=M,则QNu≠0。
事实上,如果QNu=0,则QNu=0正是方程(5)μ=1的情形,根据引理2知道,|u1|+|u2|+|u3|≤R2 定义 F:Dom L∩Ker L X[0,1]→X, 设u=(u1(t),u2(t),u3(t))T∈∂Ω∩Ker L,u为R3+中的常值向量,满足|u1|+|u2|+|u3|=M,因此F(u1,u2,u3,μ)≠0。令J=I,根据拓扑度同伦不变定理,可知 的唯一解。根据Gaines-Mawhin's重合度原理[6],可知系统(8)至少存在一个ω-周期解。也就是系统(6)至少存在一个ω-周期解。 另一方面,如果(x*(t),y*(t),z(t))T为系统(6)的ω-周期解,则根据条件(3),可知 也是ω-周期的,因此(x*(t),y*(t),z(t),z(t))T为系统(2)的一个周期解。 本文构造了一类成年食饵具有扩散和年龄结构的比率依赖型时滞微分模型,利用Gaines-Mawhin's重合度原理,获得了该系统存在周期解的充分条件。关于系统(1),文献[3]已经获得了该系统的一致持久性条件。利用此结论,通过构造合适的Lyapunov泛函,可以证明该系统周期解的全局吸引性。 [1]Xu R,Chen L S.Persistence and stability for two-species ratio-dependent predator-prey system with time delay in a twopatch environment[J].Computers Math.Applic.,2000,40:577-588. [2]Xu R,Chaplain M A J,Davidson F A.Persistence and periodicity of a delayed ratio-dependent predator-prey model with stage structure and prey dispersal[J].Applied Mathematics and Computation,2004,159:823-846. [3]刘艳伟,司军辉.一类具有年龄结构的非自治扩散系统的持久性[J].周口师范学院学报,2010,27(2):20-24. [4]Arditi R,Ginzburg L R.Coupling in predator-prey dynamics:Ratio-dependence[J].Journal of Theoretical Biology, 1989,139:311-326. [5]Chen S H,Wang F,Young T.Positive periodic solution of two-prey ratio-dependent predator-prey system with time delay in two-patch environment[J].Applied Mathematics and Computation,2004,150:737-748. [6]Gaines R E,Mawhin J L.Coincidence Degree and Non-linear Differential Equations[M].New York:Springer,1977.



2 结语

