高斯投影独立坐标系投影面和投影带选取算法的研究

王 辉

(四川省测绘产品质量监督检验站，四川成都610041)

一、引 言

按照城市测量规范、工程测量规范等规范要求，城市、工程平面坐标系统的选择，应以长度变形值不大于2．5 cm/km为原则。当长度变形值不大于2．5 cm/km时，应采用统一的高斯-克吕格投影(简称高斯投影)3°带平面直角坐标系。当投影变形值超过规范要求时，通常采用增加抵偿高程面或改变中央子午线的方式建立高斯投影的平面直角坐标系。

然而，采用严密的计算公式计算投影变形值需要计算参考椭球的几何量、曲率半径等，还要进行高斯投影坐标正算等，计算过程复杂，需要一定的大地测量学基础。某些项目，为了简化计算，地球曲率半径千篇一律采用一固定常数，计算方法不严密，容易出现投影抵偿面、中央子午线选取不合理或投影变形值超限的问题。为此，本文对投影变形值的技术方法进行了研究，利用曲面拟合的方式，推算出一套简单、可行的投影变形值计算公式，并通过试验分析，验证了此计算方法的精度及可行性。

二、独立坐标系统建立原理

实量边长投影到高斯投影面上的变形影响可表示为

式中，Δs1为实测边长归算到参考椭球面的投影变形值，与归算边高出参考椭球面的平均高程Hm成正比，为负值;Δs2为将参考椭球面上的边长归算到高斯投影面上的长度，与归算边两端点距离中央子午线的平均距离ym成正比，其值总为正。消除或减弱投影变形的思路，就是改变Hm或ym来调整Δs1、Δs2的数值大小，利用正、负抵消的原理削弱边长的投影变形，即通过增加抵偿高程面或改变高斯投影中央子午线位置的方法来消弱投影变形。

三、简易算法研究

1．常规算法

Δs1通常由下列公式计算得到

式中，s为归算边的长度，计算每公里投影变形时取值1000m;R为归算边方向参考椭球法截弧的曲率半径;M为子午圈曲率半径;N为卯酉圈曲率半径;A为归算边的方位角;B为归算边平均纬度;a为参考椭球的长半轴;b为参考椭球的短半轴;e为参考椭球的第一偏心率。

2．Δs1简易算法

由上一节可知，Δs1的计算过程涉及椭球的几何运算，计算较繁琐，且对于地面固定一点，Δs1由于归算边方位角不同数值并不唯一，其值域为这对工程测量计算、分析而言很不方便。若计算过程中采用平均曲率半径代替任意方位角上曲率半径，计算方法将得到简化，Δs1数值仅与地面点的纬度和大地高有关，其值也将是唯一的。通过计算分析，对于我国绝大部分陆域范围而言(大地高4000m以内、纬度18°～54°之间)，利用平均曲率半径计算Δs1与利用任意方向曲率半径计算的Δs'1差值在1mm以内，对分析投影变形值Δs1几乎没有影响。

为了简化算法，采用二次曲面拟合方式，利用在纬度0°～90°、大地高0～4000m之间均匀分布的14 661个点位上的Δs1值，计算得到Δs1的简化计算公式为

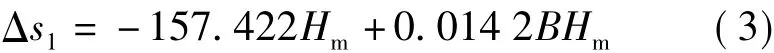
式中，B为纬度，单位为度;Hm单位为km，Δs1单位为mm。

此公式适用于在2000国家大地坐标系、1980国家大地坐标系、1954北京坐标系采用的椭球体上计算边长归算到参考椭球面的投影变形值。当大地高低于4000m时，利用式(2)在上述3个椭球面上计算Δs1的最大残差为0．46mm。拟合残差如图1所示。

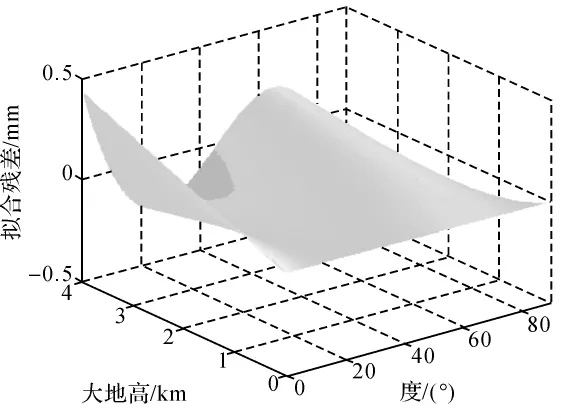
图1

四、Δs2简易算法研究

1．Δs2常规算法

Δs2常规算法公式为

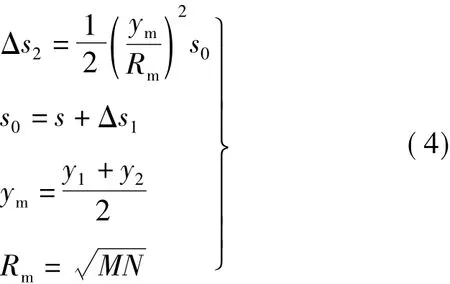
式中，Rm为参考椭球平均曲率半径，y1、y2为归算边端点的横坐标。

2．Δs2简易算法

简易算法的推导，也是利用了曲面拟合的方法。考虑到我国陆域范围主要在北纬18°～54°之间，通常独立坐标系不会超过100 km范围(此时Δs2变形值大于10 cm)，曲面拟合时利用了均匀分布在纬度18°～54°、距离中央子午线150 km(经差0°～1．5°)之间的 19 783 个点位上的 Δs2。拟合的曲面方程为

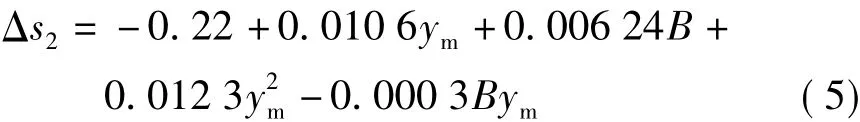
式中，B为纬度，单位为度;ym单位为 km;Δs2单位为mm。

此公式适用于在2000国家大地坐标系、1980国家大地坐标系、1954北京坐标系采用的椭球体上计算边长归算到参考椭球面的投影变形值。当与中央子午线距离小于150 km(经差小于1°30')时，利用式(5)在上述3个椭球面上计算Δs2的最大残差为0．73mm。拟合残差如图2所示。

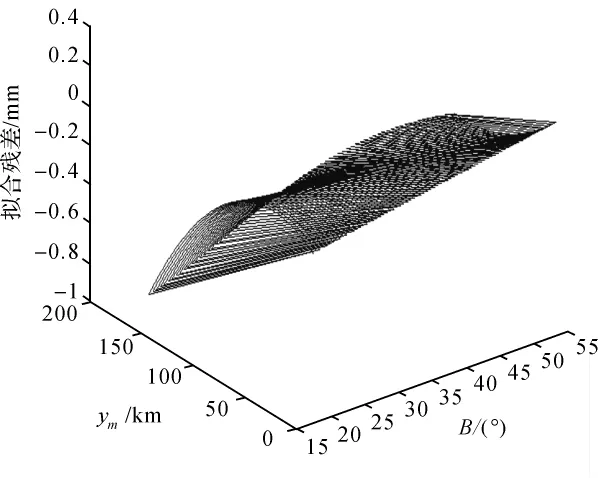
图2

五、每公里投影变形值公式

将式(3)、式(5)相加，即得每千米投影变形值简化公式为

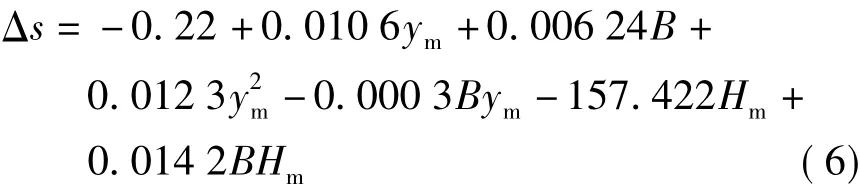
六、算 例

某测量项目，测区平均海拔为1155 m，平均纬度为26°46'，最边缘距离标准3°带中央子午线距离为50．3 km，则有

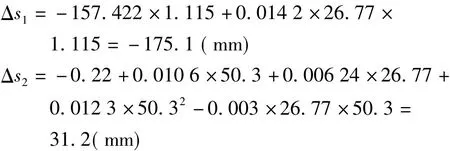
所以，Δs=Δs1+Δs2=143．9mm

显然，每千米长度变形值超过允许值2．5 cm。

此时，需改变中央子午线位置，选择一个合适的高程参考面，使得长度变形值小于限差要求，可视Hm为变量，让Δs1等于Δs2，即

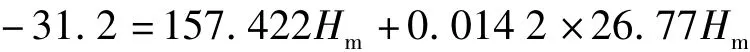
计算得到Hm值为0．199 km，这就是说，将地面实测距离归算到1155-199≈955m的高程面上，长度变形值得到完全补偿。

七、结束语

本文所提出的边长投影变形值算法，不用计算椭球参数、即可进行高斯投影正算，算法简单，易于操作。在算法推导过程中，使用了我国常见的2000国家大地坐标系、1980国家大地坐标系、1954北京坐标系采用椭球进行推导，算法通用性较好。通过拟合残差分析，本算法计算得到的Δs1实测边长归算到参考椭球面的投影变形值和Δs2参考椭球面上的边长归算到高斯投影面上的长度变形值误差优于1mm，具有较高的精度，在独立坐标系建立工作中能得到很好的应用。

[1]武汉测绘科技大学测量平差教研室，测量平差基础[M]．3 版．北京：测绘出版社，1996．

[2]孔祥元，郭际明，刘宗泉，大地测量学基础[M]．武汉：武汉大学出版社，2006．