应用拟合推估法建立我国大陆地壳水平运动速度场的研究

曾安敏，刘光明，秦显平，唐颖哲

(1．信息工程大学地理空间信息学院，河南郑州450052;2．地理信息工程国家重点实验室，陕西西安710054;3．西安测绘研究所，陕西 西安710054)

一、引 言

中国大陆除遭受印度板块的强烈碰撞以及菲律宾板块、太平洋板块的俯冲影响外，板块内形变也非常复杂和不均匀[1-3]。在具有如此复杂的地壳运动背景的大陆构建大地测量坐标框架，必须顾及板块的整体运动和局部运动。我国已建立了2000中国坐标系CGCS2000[4-6]，2008年8月正式启用相应 的 参 考 框 架 CTRF2000[6-7]。 但 由 于 建 立CTRF2000时的资料截止到2002年，重复观测时间较短，绝大部分框架点未赋予点位速度场信息，无法反映我国坐标框架的动态变化，不能完整地表述我国坐标系统的现势性[8-9]。由于板块运动引起的坐标变化是不容忽视的，速度场数据成为现代大地测量不可或缺的基础性数据。地壳运动的描述往往采用欧拉矢量法和统计拟合的方法。基于实测速度信息可以采用最小二乘准则求得欧拉矢量的估值，常用的统计拟合方法有多面函数法、有限元插值法、拟合推估法等。近10年来，国内不少学者在2002年前利用“网络工程”数据陆续开展我国大陆板块运动相关研究工作[10-12]，但由于使用数据少，其成果的实用价值有一定的局限性。2009年前利用“网络工程”数据研究了最新的速度场，有学者利用局部欧拉矢量法建立了3度格网平均值[13]，但用于建立局部欧拉矢量的点及其分布是其关键。也有学者利用有限元法建立了速度模型[14]，但面元的确定是关键。多面函数法的关键是节点的选择、核函数的确定以及平滑因子的优化，在实践中很难实践，需要依靠大量的试验。最小二乘配置法具有理论上的严密性，可综合顾及非随机参数和随机信号，在重力场的拟合与推估有成功应用[15]。在速度场的建立中，为顾及各局部形变场的变化信息，也可采用拟合推估法，拟合推估法的关键是信号向量协方差函数的确定[16]。也有研究团队利用自适应拟合推估模型[17]建立了中国大陆地壳水平运动[18]，从随机模型误差的角度通过方差因子部分调整协方差函数的不可靠问题，需要迭代计算。

本文尝试将欧拉矢量作为函数模型的趋势项，将局部形变作为函数模型的信号项，从随机信号协方差函数的建立着手，以建立与观测向量的随机误差相匹配的随机信号向量协方差函数，通过建立相对合理的函数模型和随机模型来构建中国大陆坐标速度场模型。

二、板块运动的拟合推估模型

设测站的n×1维速度观测向量为L，相应的误差向量为e，其期望为E(e)=0，协方差矩阵为;X为3×1维的板块运动欧拉矢量，S为具有先验统计特性的u×1维信号向量，协方差矩阵为。描述研究区域速度观测向量的空间分布性与离散度和分别为e和S的权矩阵。块体运动的拟合推估方程为

式中，A为n×3阶列满秩设计矩阵;B为n×u维系数矩阵。

相应的误差方程为

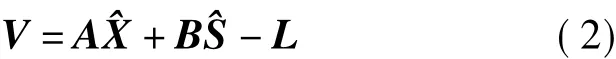
假如事先去除趋向性参数部分，仅保留随机信号部分，则式(1)改写为

其相应的误差方程也改写为

构造如下极值条件

如果同时考虑未测点信号^S'，保留 ^S'与 ^S相关性，则式(6)的拟合推估解为

通常情况下B=I，如果不考虑观测噪声，即Σe=0，则有

三、板块运动的趋势项

理论上，点位坐标变化速度与板块运动、地心运动等地球动力学因素有关。点位坐标的变化可分解为水平变化和高程变化，但是由于目前用于监测点位变化的空间技术在垂直方向的精度较低，在拟合推估时若采用三维地心坐标，可能会因为垂向站速度误差的影响点位变化的拟合推估精度，因此实践中仅考虑站心速度的水平分量。若仅考虑板块运动对点位坐标的影响，则站坐标的水平运动与板块运动的欧拉矢量的关系为：

式中，R表示地球半径;λ、φ为点的经纬度。

选择不同的板块运动物理模型可计算得到点位的不同板块运动速度，即测站的趋向性参数。从点位实测速度扣除板块运动物理模型获得的速度，则点位剩余速度为

四、协方差函数的拟合

在拟合推估中，关键的问题是在数据处理前已知协方差矩阵ΣS、ΣSS'，而协方差矩阵中的元素是根据协方差函数计算的。基于地壳连续变形的假设，在空间上很靠近的两个站点的速度值必然相关性强，反之则弱。可以设地壳运动场两点间的协方差为距离的连续函数，随机信号协方差函数可采用Gauss指数函数、Hirvonen函数等。协方差函数的Hirvonen函数为

协方差函数的Gauss指数函数为

式中，C0、k为待定常数;C(d)为 i、j两点之间的协方差;d为i、j两点之间的距离。

一般来讲，信号的初始方差可按下式计算

式中，n为距离间隔为d的点对个数;li、lj为距离间隔为d的点对的去中心化观测值，即由式(10)获得的点位剩余速度。考虑观测噪声Ce(0)，同时假设噪声e、信号S之间独立，有

由于li、lj点对间距离dij严格等于距离间隔d的点对较少，因此实际计算时，可选择落在距离间隔d一定误差范围Δd内的点对即可，即li、lj点对间距离dij满足|dij-d|=Δd的点对认为是距离间隔d的点对。然后按一定的准则估计式(11)、式(12)中的待定常数 C0、k，由式(14)可计算观测噪声方差Ce(0)。

采用“地壳运动观测网络工程”直到2008年的观测数据获得的扣除板块运动的实测速度作为信号协方差函数的观测数据。在实际应用中，通常不考虑观测噪声Ce(0)，表1给出了不顾及观测噪声的不同协方差函数系数;图1、图2为不顾及噪声的距离-协方差分布。表2给出了顾及观测噪声的不同协方差函数系数;图3、图4为顾及噪声的距离-协方差分布。可以看出，顾及观测噪声时拟合的协方差函数与实测速度的拟合程度高。另外，由于按站间距离分档计算中短距离的站点分布较少，噪声偏大，使协方差分布在中短距离的区间吻合程度降低。

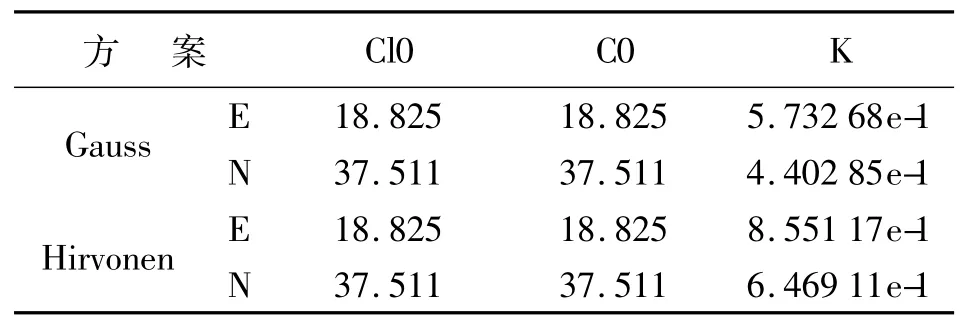
表1 不顾及噪声的协方差函数系数

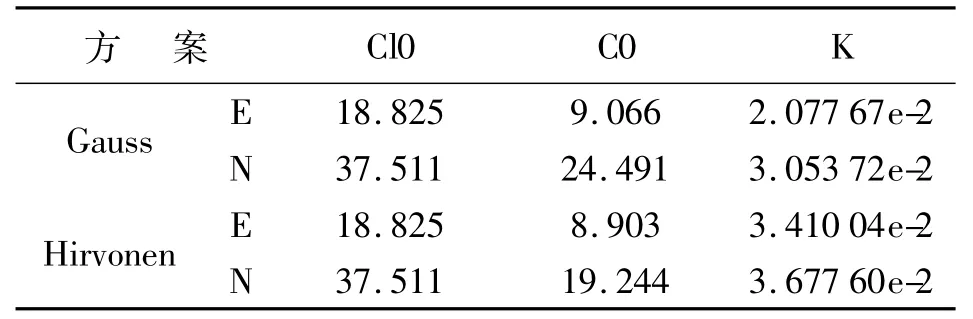
表2 顾及噪声的协方差函数系数

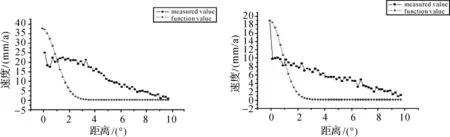
图1 不顾及噪声的Gauss函数

图2 不顾及噪声的Hirvonen函数

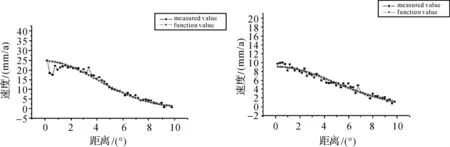
图3 顾及噪声的Gauss函数

图4 顾及噪声的Hirvonen函数

五、点位坐标速度的最小二乘拟合推估解

本文采用“地壳运动观测网络工程”直到2008年的观测数据进行点位坐标速度拟合，包括29个连续运行基准站和站速度优于3mm/a的1041个重复观测站。由于29个连续运行基准站大都建设在基岩上，其站速度是经过长期观测数据计算得到的，具有较高的精度。因此，把这29个连续运行基准站作为外部检查点，只用来评定所构建的速度场模型的精度。采用1041个重复观测站构建速度场模型，共设计了6种计算方案：

1)不考虑随机信号的板块运动模型最小二乘解;

2)利用实测速度不考虑观测噪声建立信号协方差函数，不考虑板块运动模型的拟合推估解;

3)利用实测速度考虑观测噪声建立信号协方差函数，不考虑板块运动模型的拟合推估解;

4)利用实测速度经过板块运动模型中心化后的剩余速度，在不考虑观测噪声情况下建立信号协方差函数(即表1中的高斯函数参数)，无系统性参数的拟合推估解，即采用(4)式;

5)利用实测速度经过板块运动模型中心化后的剩余速度，在考虑观测噪声情况下建立信号协方差函数(即表2中的高斯函数参数)，无系统性参数的拟合推估解，即采用(4)式;

6)在方案5基础上，考虑板块运动模型的拟合推估解，即利用表2中的高斯函数，按式(2)进行计算。

各种方案的残差统计见表3，外部检查结果见表4。分析上述结果，可以得出以下结论。

表3 残差统计 mm/a

表4 29个基准站外部检查精度 mm/a

1)从残差看，基于板块运动模型的最小二乘解的残差非常大，最大达到30 mm/a;统计精度也差，东方向4．63为mm/a，北方向6．19为 mm/a。从外部检查点来看，欧拉矢量最小二乘解的外部精度中，东方向为3．92mm/a，北方向6．59 为mm/a。这是因为欧拉矢量最小二乘解只确定了倾向性部分即参数部分，并未顾及局部的系统性变化。

2)利用实测速度原始观测数据(即不经过去中心化处理)，在建立协方差函数中无论考虑观测噪声与否，是否考虑板块运动模型，拟合推估解效果都很差(见方案2、3。方案2外部检查RMS在北方向为5．07mm/a，东方向为6．33mm/a;最大值在北方向为22．90mm/a，东方向为 18．68mm/a。方案 3 外部检查 RMS在北方向为 3．85 mm/a，东方向为7．21mm/a;最大值在北方向为 9．70 mm/a，东方向为18．79 mm/a。这是因为在拟合推估模型中要求对数据进行去中心化处理，即去掉倾向性参数的影响，否则不消去倾向，就会产生畸变。

3)经过去中心化数据处理后得到剩余速度，在建立协方差函数中考虑观测噪声与否，对拟合推估解影响很大(见方案4、5)。不考虑观测噪声，方案4外部检查RMS在北方向为4．45 mm/a，东方向为4．25mm/a;而考虑观测噪声的方案5外部检查RMS 在北方向为 1．93mm/a，东方向为 1．76mm/a。综合方案2、3结果，说明倾向性参数是存在的，与板块整体运动这一物理现象是一致的，同时也说明观测噪声是存在的。

4)考虑观测噪声，利用去中心化数据处理后得到剩余速度建立协方差函数，无论是先计算趋向性参数部分(方案5)，还是在模型中考虑趋向性参数部分(方案6)，计算结果精度一致，精度都非常高，内外部精度一致，北方向和东方向都优于2mm/a。这是因为建立的函数模型和随机模型都相对合理，在函数模型方面，同时考虑了倾向性参数部分和随机信号。在随机模型方面，在建立随机信号协方差函数时经过了中心化数据处理，并顾及了观测噪声，这使得信号协方差函数与观测噪声协方差具有较好的协调性。

[1]李延兴，张静华，李智，等．由GPS网融合得到的中国大陆及周边地区的地壳水平运动[J]．测绘学报，2003，32(4)：301-307．

[2]朱文耀，王小丫，符养，等．基于ITRF2000的全球板块运动模型和中国的地壳形变[J]．地球物理学报，2002，45(S0)：197-204．

[3]王敏，沈正康，牛之俊，等．现今中国大陆地壳运动与活动块体模型[J]．中国科学(D 辑)，2003，33(B04)：21-32．

[4]陈俊勇．中国现代大地基准：中国大地坐标系统2000(CGCS2000)及其框架[J]．测绘学报，2008，37(3)：269-271．

[5]魏子卿．2000中国大地坐标系[J]．大地测量与地球动力学，2008，28(6)：1-5．

[6]YANG Yuanxi．Chinese Geodetic Coordinate System 2000[J]． Chinese Science Bulletin， 2009，54(15)：2714-2721．

[7]陈俊勇，杨元喜，王敏，等．2000国家大地控制网的构建和它的技术进步[J]．测绘学报，2007，36(1)：1-8．

[8]王敏，张祖胜，许明元，等．2000国家GPS大地控制网的数据处理和精度评估[J]．地球物理学报，2005，48(4)：817-823．

[9]YANG Yuanxi，TANG Yungzhe，CHEN Chuanlu，et al．Integrated Adjustment of Chinese 2000’GPSControl Network[J]．Survey Review，2009，41(313)：226-237．

[10]柴洪洲，催岳，明锋．最小二乘配置方法确定中国大陆主要块体运动模型[J]．测绘学报，2009，38(1)：61-65．

[11]江在森，刘经南．应用最小二乘配置建立地壳运动速度场与应变场的方法[J]．地球物理学报，2010，53(5)：1109-1117．

[12]刘经南，姚宜斌，施闯．中国地壳运动整体速度场模型的建立方法研究[J]．武汉大学学报：信息科学版，2002，27(4)：331-336．

[13]魏子卿，刘光明，吴富梅．2000中国大地坐标系：中国大陆速度场[J]．测绘学报，2010，39(4)：403-410．

[14]蒋志浩，张鹏，秘金钟，等．基于CGCS2000的中国地壳水平运动速度场模型研究[J]．测绘学报，2009，38(6)：471-476．

[15]TSCHERNING C C．Collocation and Least Squares Methods as a Tool for Handling Gravity Field Dependent Data Obtained Through Space Research Techniques[R]．Paris：[s．n．]，1978：141-149．

[16]YANG Yuanxi．Robustfying Collocation[J]．Manusctipta Geodactica．1992，17(1)：21-28．

[17]Yang Y，Zeng A，Zhang J．Adaptive Collocation with Application in Height System Transformation[J]．Journal of Geodesy，2009，83(5)：403-410．

[18]杨元喜，曾安敏，吴富梅．基于欧拉矢量的中国大陆地壳水平运动自适应拟合推估模型[J]．中国科学：地球科学，2011，41(8)：1116-1125．