几何精度因子对GPS定位结果的影响

于 军，邓明镜，王星星

(1．中国华粮物流集团北良有限公司，辽宁大连116001;2．重庆交通大学土木建筑学院，重庆400074)

一、引 言

几何精度因子(geometric dilution of precision，GDOP)是衡量定位精度的一个很重要的系数，它代表GPS测距误差造成的接收机与空间卫星间的距离矢量放大因子。实际表征参与定位解的从接收机至空间卫星的单位矢量所勾勒的形体体积与GDOP成反比。

GDOP分量包括PDOP(3维位置的几何精度因子)、HDOP(水平几何精度因子)、VDOP(垂直几何精度因子)、TDOP(时间几何精度因子)。这些GDOP项中的每一个均可单独计算，但它们是由协方差得到的，故相互间并不独立。例如，一个高的时间几何精度因子(TDOP)会引起大的接收机时钟误差，最终会导致位置误差[1]。

需要注意的是，好的GDOP不一定会有高的定位精度，如图1所示。虽然接收机与卫星分布间的几何图形很好，但由于接收机周围有地形地物遮挡，使其可见性受到阻碍，收不到卫星信号。条件恶劣时，甚至收不到足够数量的卫星信号，无法实现定位。因此，好的GDOP碰上坏的可见性，则定位精度会受损。

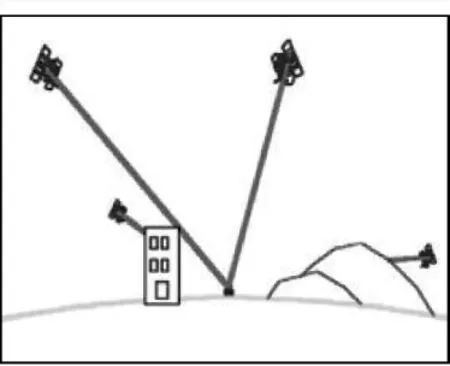
图1 好的GDOP与坏的可见性情况

二、GDOP计算原理

在GPS数据处理中，GPS方程的最终求解结果可表达为

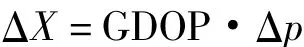
式中，ΔX为位置(求解域)误差;Δp为观测量误差;GDOP为几何精度因子，它与用户和定位星座间的几何关系有关。

设某时刻用户同时观测到n颗卫星，并建立了如下伪距观测方程

式中，Ri为用户到GPS卫星的几何距离;τ为用户接收机的时钟偏差;τi为GPS卫星时钟偏差;c为光速;为 GPS 卫星星历误差;和分别为电离层误差、对流层误差和多路径误差;v为接收机噪声误差。

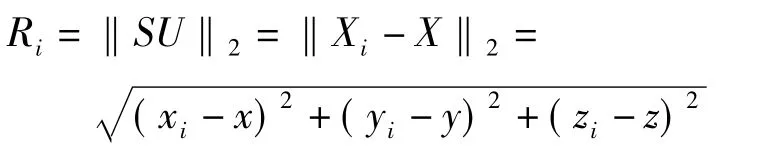
对伪距观测方程，考虑星钟、电离层、对流层误差校正后，可进一步写为

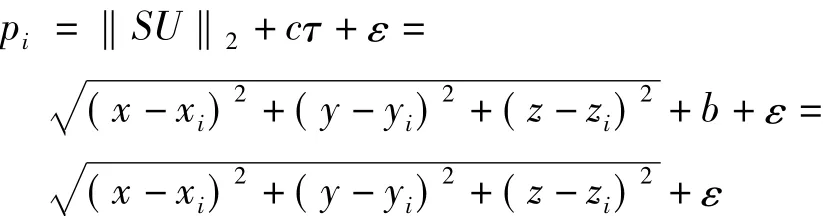
由于‖·‖为非线性运算，则在某一估计点U0(x0，y0，z0，b0)作泰勒级数展开并取一阶近似，有

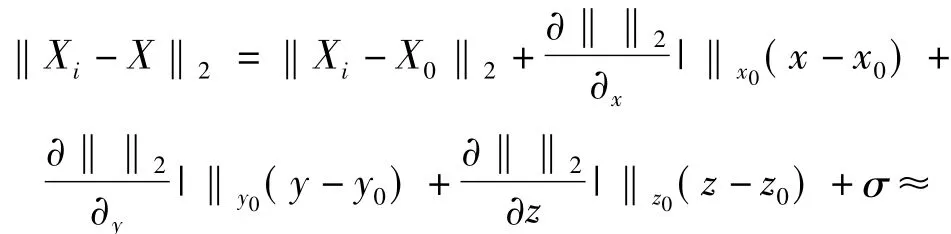
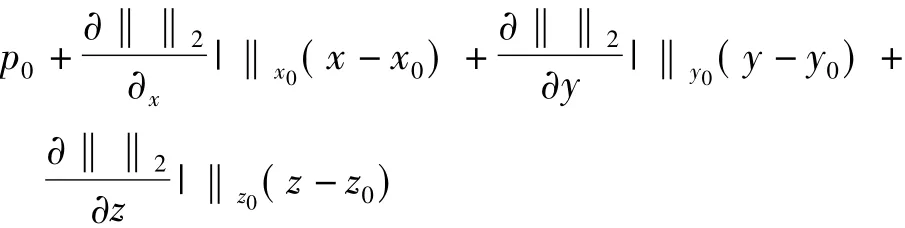
其中，p0= ‖Xi-X0‖2。所以

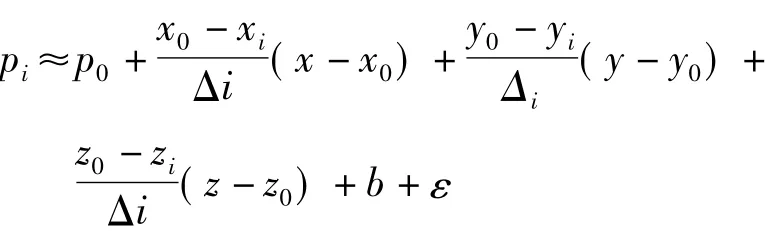
1.资本成本决策工作前期：在这一时期，数据模型在三维模型的基础上，搭建一个有效的管理平台，实现基于模型的可视化操作，并达到多方协同工作的效果；2.资本成本决策工作中期：在这一时期，可以对管理工作进行合理的进度管控、质量管控，并进行有效的成本管理，并进行成本清单标准化；3.资本成本决策工作后期：在这一时期，可资本成本鞠策标准深化应用，实现对多项目的综合管理，并且可以对历史数据进行累计保存。

进一步有

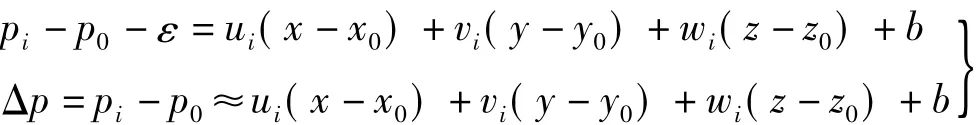
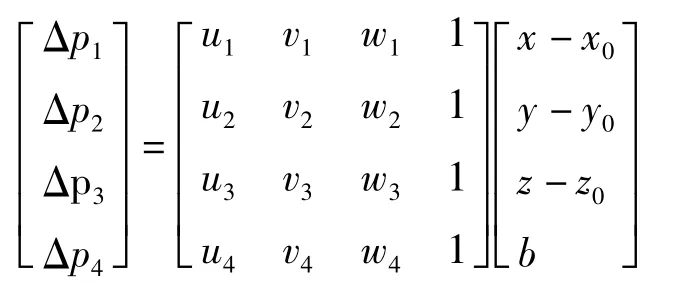
进一步简写为

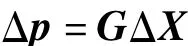
若矩阵G满秩，则

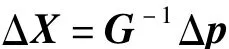
对4颗以上的可见星，利用最小二乘法，可得

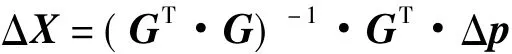
取X=X0+ΔX进行迭代计算，直至一般的，取error为10-2，上述计算在3～4步内即收敛于真值[3]。

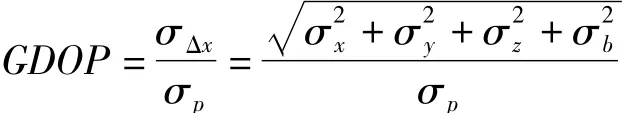
设观测量的观测误差矢量为δp，定位误差矢量为δX，则δX的协方差矩阵为

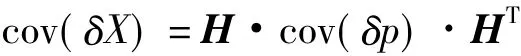
进一步设接收机到各颗可见卫星的观测误差独立同分布，且方差为，则有

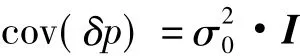
式中，I为单位矩阵。因此

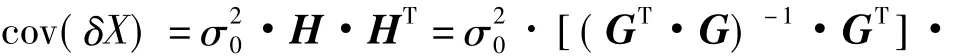
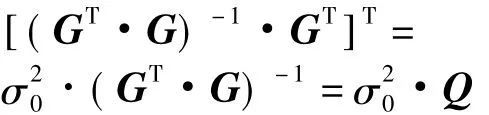
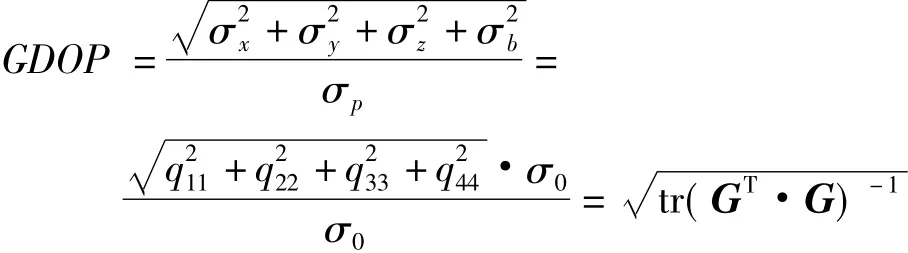
类似地，可定义位置几何因子为

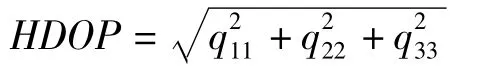
三、GDOP对GPS定位结果影响的规律分析

实际上，GDOP的数值越大，所代表的单位矢量形体体积越小，此时的GDOP会导致定位精度变差。好的GDOP，是指其数值小，代表大的单位矢量形体体积，从而得到高的定位精度。在作业规划中，GDOP通常是由卫星历书和接收机估算位置计算出来的。本文通过对试验观测所得的多组数据进行处理并对各个基线的E级网精度限值进行分别计算，将各基线的GDOP值分别进行统计，其结果如图2、3所示，一般情况下，当GDOP值越小时，所得的GPS定位结果精度越高;当GDOP值越大时，所得的GPS定位精度越低，但是在大部分情况下都能满足所要的精度要求。

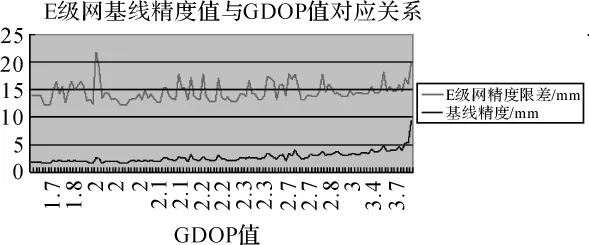
图2 E级网基线精度值与GDOP值对应关系

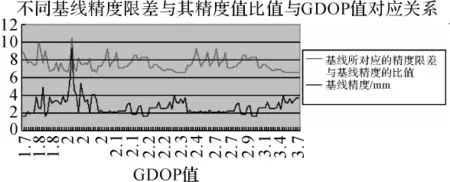
图3 不同基线精度限差与其精度值比值和GDOP值的对应关系

对于通常所用的测图网，即GPS的E级网，在GDOP≤6的情况下均能满足精度要求，且，当需要更高的定位精度时，在控制PDOP值的同时也对GDOP值进行了有效的控制。通过对解算数据进行分析对比研究，当GDOP≥3时，各基线的相对精度有所降低，并随着GDOP值的增大，呈逐渐降低的趋势。因此，可以通过对图3研究结果综合分析可得，当所需GPS定位精度较高时，将GDOP值限制在不大于3的观测条件之下(当然越小越好)，将会对提高观测精度有非常大的帮助，对观测数据质量将会有一个大的提升。

四、结束语

经过对试验观测所得的多组数据进行处理并进行研究分析表明，一般情况下，当GDOP值越小时，所得的GPS定位结果精度越高;当GDOP值越大时，所得的GPS定位精度越低，但是大部分情况下都能满足所要的精度要求。对于一般的工程控制网，即GPS的E级网，在GDOP≤6的情况下均能满足要求，目前大多数仪器的GDOP限制值通常为8(含常数)，且，当需要更高的定位精度时在控制PDOP值的同时也对GDOP值进行了有效的控制。本文通过对几何精度因子进行研究，减少了利用PDOP值进行测量精度判断的麻木性，通过本论文研究结果可知，在需要较高精度的观测值时，利用星历预报软件选择PDOP值小于3的最佳观测时段，大大提高了工作效率，避免不必要的时间耗费。

[1]陈小平，滕云龙，康荣雷，等．几何精度因子改进算法研究[J]．电子科技大学学报，2008，37(S1)：27-30，74．

[2]张勤，李家权．GPS测量原理及应用[M]．北京：科学出版社，2005．

[3]廖春招．GPS卫星坐标计算及几何精度因子[J]．矿山测量，2011(8)：29-31．