论高速铁路与航空运输客票博弈定价

张 旭,栾维新,蔡权德,赵冰茹

(大连海事大学 交通运输管理学院,辽宁 大连 116026)

一、引 言

根据国家2008年调整的《铁路发展中长期规划》,至2020年,我国将建立时速200 km以上的客运专线1.2万km,形成"四横四纵"的高速铁路网. 2008年至今,京津城际铁路、武广高铁、沪杭高铁先后进入运营阶段,高铁的运营对同线路的空运市场形成了巨大的冲击.航空公司为争夺市场,采取了提供特价机票、增开航班等一系列措施.随着高铁线路的建设和高铁网络的逐渐完善,高铁与航空运输之间的竞争将更加激烈.

在市场经济下,高速铁路和航空运输作为自主经营、自负盈亏的经济主体,二者进行市场竞争的目标都是争夺客源以获取最大利润.客票的定价决策必然受这一目标支配,并为之服务.因此高速铁路与航空运输票价制定的合理与否将直接影响二者在高速客运市场份额的高低,同时也将影响高速客运网络的健康发展.

对于铁路票价的制定,国内外学者做了相关研究.陈建华等[1]提出了一种新的广义费用计算方法,利用logit函数建立了以铁路部门收益最大化为目标的铁路票价制定线性规划模型.Bard[2]根据经济学原理,通过对运输需求函数的分析,得到了理论上的最佳定价区间.Ferrari[3]以中长途旅客运输市场为研究对象,在运输通道方面提出了客货分线运输的想法,并相应建立了以运输企业利润最大化为目标的多层线性规划模型.一些文献[1,4-6]利用灵敏度分析的求解方法,分析不同运输方式的旅客流量与运价之间的联系.以运输企业效益最优与旅客出行广义费用最小化的均衡为目标建立双层规划模型,充分考虑到不同收入层次的旅客对交通方式的选择与铁路运输通道合理分工的协调.Gallego等[7]根据系统动力学的原理,建立了高速铁路运价制定的系统动力学流程图,以京沪高铁为虚拟背景进行了模拟仿真.

从现有的研究成果来看,对于铁路运输竞争对手的选择多以公路为主,铁路的定价变化过程一般都以公路固定运价为前提进行分析,这与价格制定的动态过程是相悖的.同时高速铁路作为新兴产物,其平均运输速度达到200 km/h,这是公路运输无法达到的,因此对于高铁的运价制定应选取新的竞争对手进行分析.本文在借鉴相关研究成果的基础上,将航空运输作为高速铁路的竞争对手进行竞争定价分析,在阐述博弈理论在高铁与航空运输定价过程中应用的基础上,根据完全信息动态博弈对高铁与航空运输动态定价过程进行描述,建立了高铁与航空运输动态博弈定价模型,运用灵敏度分析的方法进行求解,得出高铁与航空运输博弈定价区间,为票价制定部门的客票定价决策提供依据.

二、博弈理论在高速铁路与航空运输定价中的应用

博弈是指一些相互依赖、相互影响的决策行为及其结果的组合.研究相互依赖、相互影响的决策主体的理性决策行为以及这些决策的均衡结果的理论称为博弈论(game theory)[8].博弈的基本组成要素为参与人、行动、信息、策略、收益.其中信息是指博弈参与人的知识、理性、行动、决策能力等.按照博弈的形式可以将博弈分为合作博弈和非合作博弈两种.在非合作博弈中,按照信息的掌握情况及博弈的过程可分为完全信息静态博弈、完全信息动态博弈、不完全信息静态博弈、不完全信息动态博弈四种.

三、高速铁路与航空运输动态博弈定价模型

如前文所述,高速铁路与航空运输的运价竞争可以认为是一个动态博弈,而动态博弈的过程是由若干个静态博弈所组成的,因此首先考虑在航空运输票价不变的前提下高铁票价的制定.把高铁票价的决策部门看做是指导者(leader),在此票价下的旅客出行方式选择或者高铁及航空的交通流量可看做是跟随者(follower).高铁票价制定部门根据运输的成本和对收益的期望来制定票价,从而影响旅客对于出行方式的选择.而旅客根据自身对运价的承受能力、自身需求、个人喜好等方面来选择运输方式.这种关系可以用双层线性规划来进行描述,其基本思想如下面数学模型:

式中 y(x)由下层模型给出:

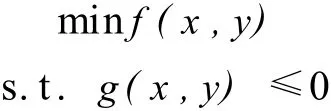
F是上层规划的目标函数,用来表示高速铁路营运部门的利润;x为上层规划的决策变量(即高速铁路的票价);f是下层规划的目标函数,用来表示旅客出行的广义费用;y为下层规划的决策变量(即不同运输方式的客流量);y(x)为上层规划决策变量的函数.F作为高铁的利润函数,可用运输成本及运输收入两部分来表示,则上层规划可表示为

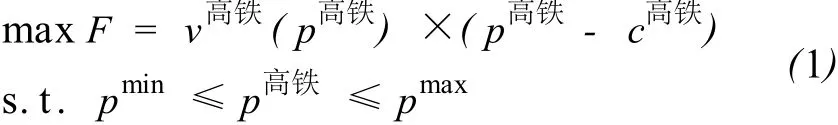
式中c高铁表示高速铁路的单位运输成本,这里假设为常量,pmin,pmax分别表示管理部门所允许的票价下限和票价上限.v高铁(p高铁)由下层规划给出,假设旅客流量变化被看做是一个连续的过程,则下层规划表示为

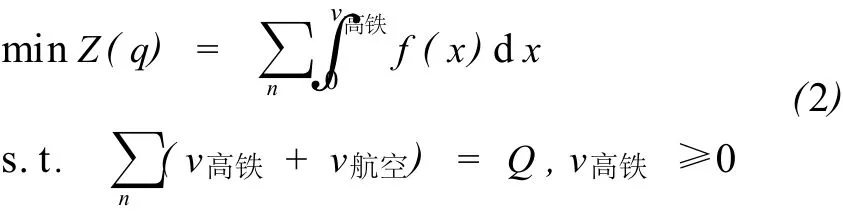
式中 v高铁表示高速铁路的客流量,用logit函数表示.f(x)为广义费用函数,广义费用函数一般采用幂函数或对数函数的表示方法,本文采用幂函数的表示方法[2],形式如下:

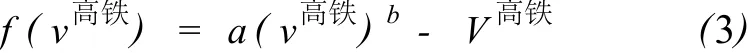
式中a,b为参数,v高铁表示高铁这种客运方式能够观测到的效用值或者是对旅客的吸引程度,效用值越高,表示旅客选择此种交通方式所获得的利益就越大,本文用以下式子表示效用值:

变频发电方式是采用变频装置，将水泵在低速状态下发出的低于电网频率、电压的电能转换为和电网频率、电压相同的电能。该发电方式可以使水泵运行在发电高效区，水泵机组本身不需要增加辅助设备，电机的保护及励磁功能仅需作一些技术上的调整，但需要增加1套变频设备以及相应的厂房。

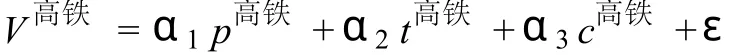
由式(1)～(4),可以建立航空票价固定时高速铁路的定价优化模型,即

同理,可以建立高速铁路票价固定时航空运输的定价优化模型,即

如上文所述,高速铁路与航空运输的竞争定价过程是一个完全信息动态博弈的过程.高速铁路作为新的参与者,根据自身的建设及经营情况,确定运输价格为,航空运输观测到,结合航空票价,代入式(6),航空运输就确定了一个在下的航空票价,这样航空运输形成了一个价格策略 ().高铁在航空新的价格策略(,)下,代入式(5),确定一个在下的高铁票价,同理高铁形成了一个新的价格策略().经过一轮博弈,高速铁路与航空运输形成了一个新的运价策略,即().以此类推,高速铁路与航空运输经过n轮运价博弈,形成了一个运价策略集{(),(),…, ()}.双方经过运价博弈,最终运价趋于纳什均衡,形成最优运价策略().

四、基于灵敏度分析的多层规划求解

通过对式(5)、(6)组成的多层规划问题的求解,可以找到大致合理的高速铁路和航空运输的运价,以达到决策部门的目标.多层规划模型是由式(5)、(6)两个双层规划组成的,因此,需先对式(5)、(6)求解.双层规划问题一般都是非凸的,所以在求解的过程很难求得最优的全局解.同时由于双层规划是一个非确定性多项式难题,目前不存在多项式精确求解的算法,因此在实际求解过程中,为简化求解过程,一般采用模拟退火算法(simulated annealing algorithm)、人工神经网络(artificial neural network)、禁忌搜索(tabu search)、蚁群算法(ant algorithms)等启发式方法.

求解文中双层的规划的关键问题在于找到反应函数 v(p)的具体形式,灵敏度分析可以得出在多运输模式下的某种运输方式的客运量对客运票价的导数关系,再运用泰勒展开式对 v(p)进行线性逼近,从而简化 v(p)以提高对双层规划的求解效率,这就是基于灵敏度分析的启发式算法(SAB).本文采用SAB算法对多层规划求解,求解算法具体步骤如下:

(7)使用灵敏度分析的求解方法找到高铁客流量对票价的导数,根据 v高铁(p高铁)=v高铁*()(p高铁-)求出反应函数 v()的近似形式.

五、高速铁路与航空运输动态博弈定价分析

在高速铁路经营过程中,运营的线路不同,客票的价格也不尽相同.同样,不同线路航空票价存在差异,即使是同一条航线,由于订票时间的不同,票价也存在折扣上的差异.因此,为使高铁和航空博弈定价具有普遍适用性,文中选取高铁和航空运输每百公里的平均运价作为博弈的参与者进行分析.在模型运算过程中,为简化计算过程,交通工具运行时间按照每百公里的运行的平均时间计算,旅客的总数假定为10 000人.同时,部分参数的选取在参考相关学者的研究以及相关观测数据统计校正的基础上进行假定.模型中相关系数标定如表1所示.

表1 相关参数

将高铁及航空的票价(45,75)作为初始值,通过计算,迭代过程中的参数和最终结果见图1和表2.

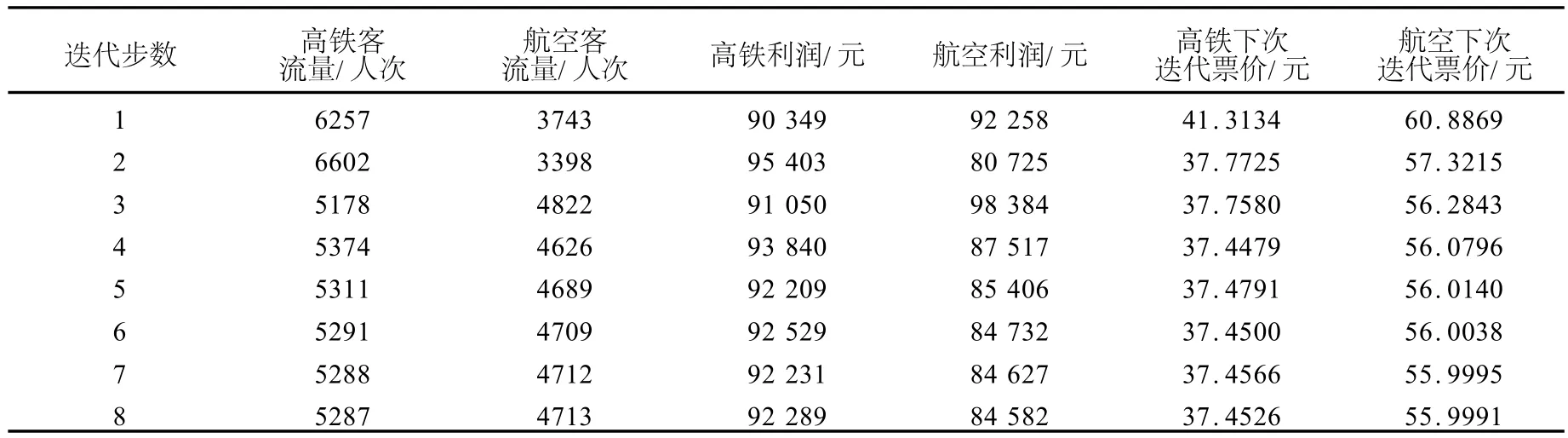
表2 高速铁路及航空运输博弈定价计算结果

从图1可以看出,经过8次迭代,运算的结果收敛,高速铁路和航空运输的博弈定价结果趋于纳什均衡的稳态,但由于双层规划是一个非凸的,采用基于灵敏度分析的多层规划求解算法,很难求得一个全局最优解.双方博弈定价的过程是一个价格战的过程,高速铁路和航空运输通过互相降低票价来吸引乘客.经过8次迭代,计算结果收敛,高速铁路趋于均衡的客票定价区间在[37元,38元],航空运输趋于均衡的客票定价区间在[55元,56元].

表2中的数据是每一步迭代过程高铁、航空的客流量、利润、迭代票价的变化过程.通过对表2的分析可以发现,随着运价的博弈,高铁和航空运输客流量及利润的变化不是线性的过程,表现出一定的波动性.高铁在第二次迭代中,客流量为6602人,利润为95 403元,达到了整个博弈过程的最大值,而航空运输的客流量为3398人,利润为80 725元,是整个博弈过程的最小值.随后航空运输为提高市场份额降低票价,在第三次博弈过程中,航空运输的客流量增加到4822人,利润上升到98 384元,达到了整个博弈过程中的最大值,降价效果显著.进入第四次博弈后,双方的客流量、营运利润、票价的变化相对平稳.在第八次博弈后,客流量、营运利润达到稳态,票价博弈的结果趋于纳什均衡.

值得注意的是,高速铁路、航空运输的客流量及收益的最大值所对应的票价,并不是最后处于纳什均衡的客票定价区间.这是因为其中一方的客流量达到最大值时,由于高速客运市场的旅客人数相对固定,另一方的客流量下降到最小值,营运利润与客流量呈现同样的变化趋势,随后客流量下降的一方必然降低票价以获得更多的客流量,提高利润.经过反复的价格博弈,双方的客流量及利润达到了一个均衡的状态,营运利润在高速铁路和航空运输可接受的区间内,双方的定价博弈结束.同时发现,进入第四次迭代后,虽然高速铁路和航空运输的票价都在降低,但高速铁路的客流量呈现线性减少,而航空运输的客流量呈现线性增加的态势.这体现的是每一次迭代过程的最终结果,实际上在每次迭代的子博弈过程(即式(5)所描述的过程)中,高速铁路的客流量的变化并不是线性降低的,也有一个客流量增加的过程,但由于受到航空运输的降价影响,因此高速铁路的客流量随着价格的降低而减少,航空运输的客流量随着价格的降低而增加.对于客运票价和客流量、利润的分析,将有助于高速铁路及航空运输的定价决策部门在决策过程中,根据客运路线长度,制定双方可以接受的均衡票价,从而避免形成以获得高客流、高利润为目标的恶性价格战,进而保证高速客运市场的健康发展.

六、结 论

本文在借鉴博弈论理论的基础上,用斯坦科尔伯格寡头竞争模型对高速铁路与航空运输的竞争定价过程进行了描述,建立了高速铁路与航空运输的竞争定价多层规划模型.通过对多层规划模型结构的分析,选择了基于灵敏度分析的启发式算法进行求解,得出了高速铁路趋于均衡的客票定价区间在[37元,38元],航空运输趋于均衡的客票定价区间在[55元,56元]的结论.随后对于每一步迭代过程中客流量、双方利润的变化进行分析,发现进入第四次博弈后,票价的变化趋于均衡,且高铁及航空的博弈定价均衡点并不是双方利润最大的票价取值点.本文的研究充分说明了博弈理论用于高铁定价的适用性,同时对于客运票价和客流量、利润变化过程的分析为定价科学性提供参考,降低了高铁与航空运输恶性价格战发生的可能性.随着旅客出行交通方式选择的日趋多样化,影响旅客出行方式选择的因素也更加复杂,因此,在以后的研究中应增加广义费用中程前程后时间、程前程后费用等交通方式选择影响因素的考虑.

[1]陈建华,高自友.合理制定铁路旅客票价的优化方法[J].铁道学报,2005(8):16-19.

[2]BARD J F.An algorithm for solving the general bi-level programming problem[J].Mathematics of Operations Research,1983,8(2):260-272.

[3]FERRARI P.Road pricing and network equilibrium[J]. Transportation Research,1995,29(3):357-372.

[4]四兵锋,高自友.铁路客票价格与客流量之间的灵敏度分析[J].铁道学报,1999(10):13-16.

[5]YANG Hai.Sensitivity analysisfor queuing equilibrium network flow and its application to traffic control[J].Mathematical and Computer Modelling,1995,22(4-7):247-258.

[6]NAGURNEY A,DONGJune.A multiclass,multicriteria traffic network equilibrium model with elastic demand[J]. Transportation Research,2002,36(5):445-469.

[7]GALLEGO G,VAN RYZIN G.Optimal dynamic pricing of inventories with stochastic demand over finite horizons [J].Management Science,1994,40(8):999-1020.

[8]ROBINSON L W.Optimal and approximate control policies for airline booking with sequential fare classes[J].Operations Research,1995,43(2):252-263.