基于理化指标统计分析的葡萄酒质量评价——2012年全国大学生数学建模竞赛A题论文

侯勇超 马松林 孙诚程 胡继元 高慧

（巢湖学院数学系，安徽 巢湖 238000）

1 问题重述[1]

确定葡萄酒质量时一般是通过聘请一批有资质的评酒员进行品评,从而确定葡萄酒的质量。酿酒葡萄的好坏与所酿葡萄酒的质量有直接的关系，葡萄酒和酿酒葡萄检测的理化指标会在一定程度上反映葡萄酒和葡萄的质量。通过给定的得分及理化指标数据解决下列问题：

（1）分析两组评酒员的评价结果有无显著性差异，哪一组结果更可信？

（2）根据酿酒葡萄的理化指标和葡萄酒的质量对这些酿酒葡萄进行分级。

（3）分析酿酒葡萄与葡萄酒的理化指标之间的联系。

（4）分析酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响，并论证能否用葡萄和葡萄酒的理化指标来评价葡萄酒的质量？

2 问题分析与预备知识

2.1 问题一

利用SPSS等统计软件对评价结果进行数据分析[2]，并采用计算均值、T-检验的方法进行计算分析，用以评判两组评酒员评价结果的差异性，从而判断评价结果可信性。T-检验是用t分布理论来推论差异发生的概率，从而比较两个平均数的差异是否显著。当总体分布是正态分布，如总体标准差σ未知且样本容量n＜30，那么样本平均数与总体平均数的离差统计量呈t分布。检验统计量为：

2.2 问题二

在第一问的基础上，选取第二组评酒师对红白葡萄酒的评价结果平均值作为标准，先通过主成分分析法[3]将问题简化，从而便于排序与分类，再使用聚类分析对主成分的特征向量进行分析。最后参考酒类等级建立标准[4]，并使用数据分析结果支持结论。

2.3 问题三

根据第二问分级结果，使用SPSS软件对葡萄酒和葡萄的主要理化指标进行相关性及多元回归分析[5]，从而确定酿酒葡萄与葡萄酒理化指标之间的联系。

2.4 问题四

根据葡萄酒评价结果与葡萄酒及酿酒葡萄主要理化指标间的关系，筛选出对葡萄酒的分有重要影响的指标，然后做多元线性回归分析，并通过数据带入对比检验后，用得出评价葡萄酒质量的公式。

3 问题假设与符号说明

问题假设：

3.1 假设原始数据基本准确（个别异常数据可进行处理）；

3.2 假设评酒员恶意打分情况可忽略，仅考虑评酒水平差别；

3.3 假设葡萄样品为随机选取，质量水平近似符合正态分布；

3.4 假设葡萄酒由与之编号相同的酿酒葡萄酿造。

符号说明：

t为样本平均数与总体平均数的离差统计量；

μ为总体平均数；

σX为样本标准差；

n为样本容量；

X″为标准化结果；

Xi样品指标 ；

Xmin指标最小值；

Xmax指标最大值。

4 模型的建立与求解

通过统计分析等方法，4.1-4.4分别建立模型解决题目中的问题。

4.1 问题1的T—检验、方差检测模型

从实际生活中，我们知道对葡萄酒的评价主要采用感官评定价法。感官评价主要依靠评酒员的个人经验来完成，所以在评判哪组评酒员的结果可信度比较高时，就必须比较对于不同的评酒师对于同一种酒的评判结果的差异性，以此为标准，哪组出现的差异比较少，哪组可信度就高。首先，我们使用了Excel和SPSS软件对两组评酒员的品尝评分进行了处理，得出了每组评酒员给出的综合分数（表1），并运用T-检验得到如下结论：

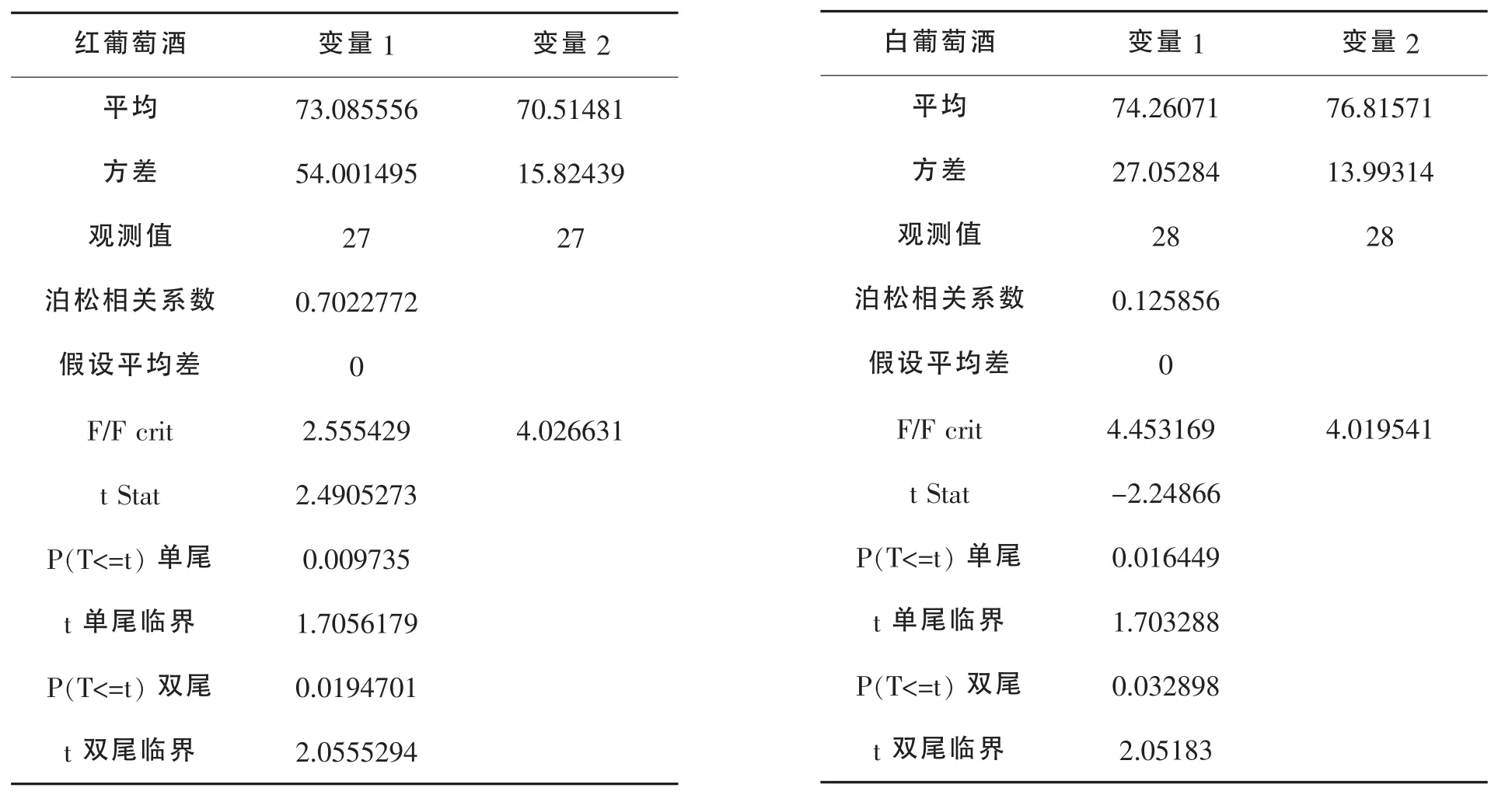
表1 红白葡萄酒T-检验结果

由上表可知两组评酒员评价结果存在显著性差异，特别由白葡萄酒的评论结果计算出P值为0.009＜=0.05且F＞F crit,所以更体现出两组评酒员评价结果的不同。

其次，我们对评价数据进行统计后，得到两组评酒员对红白葡萄酒评价结果的平均值及方差得出下表：

表2 评酒员对红白葡萄酒评价结果的平均值及方差

由上表得出结论第二组方差较第一组小，故第二组评酒师对红白葡萄酒的评价结果更为准确。

4.2 问题2的主成分分析、聚类分析模型

由第一问我们得出第二组评酒师对红白葡萄酒的评价结果更加准确，因此我们取第二组评酒师对红白葡萄酒的评价结果平均值作为第二问中的葡萄酒的质量，再据附录二中的酿酒葡萄的理化指标进行分析，找出哪种酿酒葡萄理化指标是影响葡萄酒质量的关键因素。

我们使用SPSS软件对酿酒葡萄的各项理化指标进行了一定的处理如求均值、方差等，然后对结果进行标准化处理。 由附件得到酿酒葡萄的主要成分有50多种，并且它们之间存在着复杂的关系。因此，我们需要通过主成分分析在保留主要信息的前提下对这些指标进行简化处理。

4.2.1 主成分分析过程与结果

对于红葡萄，通过SPSS 18软件对葡萄酒的30项指标进行主成分分析，得到方差分解图和主成分系数矩阵,其中前8个主成分的特征较大，且累计贡献率达84.148%，根据主成分选取指标的原则，选取前8个主成分可以代表30项指标。因此选择该 8 个主成分，并定义为 Y1，Y2，Y3，Y4，Y5，Y6，Y7，Y8。

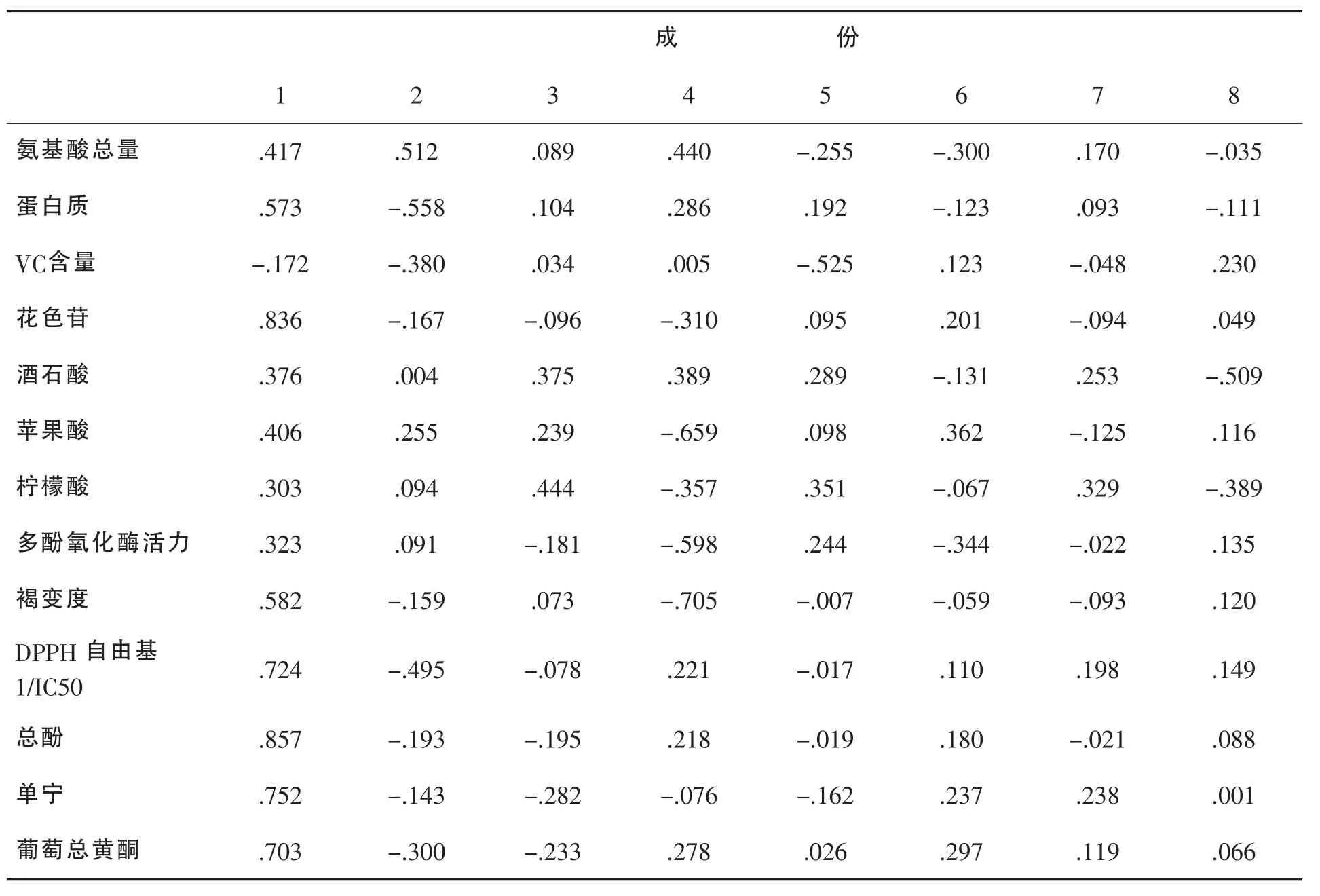
表3 成份矩阵a

a.已提取了8个成份。

对于白葡萄通过SPSS软件对葡萄酒的30项指标进行主成分分析，得到方差分解图和主成分系数矩阵。其中前9个主成分的特征较大，且累计贡献率达84.148%，根据主成分选取指标的原则，选取前9个主成分完全可以代表30项指标。因此选择该 9 个主成分，并定义为：Y1，Y2，Y3，Y4，Y5，Y6，Y7，Y8。

对于红葡萄，用表中的各个值的成份量数据除表中主成分相对应的特征值开平方根使得主成分中每项指标所对应的系数[4]，即特征向量。将得到的特征向量与标准化后的数据相乘得出主成分表达式。

第一种主成分方程：

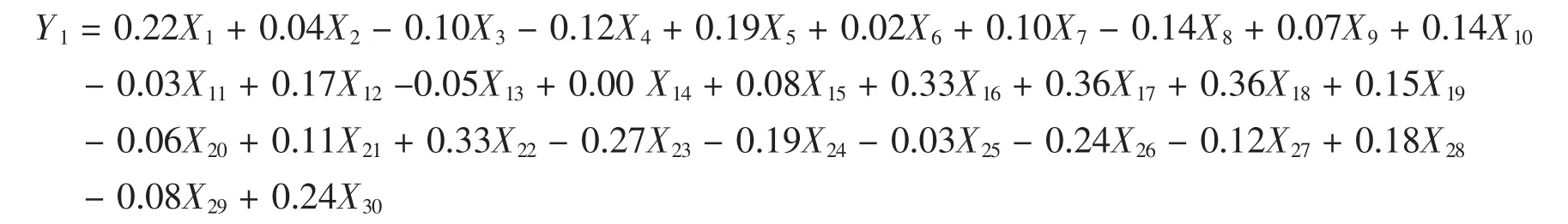
第一主成分方差贡献率最大为23.461%，通过线性方程能得出特征向量较大的是X4，X11。

第二种主成分方程：

第二主成分方差贡献率最大为16.831%，通过线性方程能得出特征向量较大的是X16，X17，X18，X22。第三主成分方差贡献率最大为12.688%，特征向量较大的是X14，X29。第四主成分方差贡献率最大为9.508%，特征向量较大的是X19。第五主成分方差贡献率最大为6.692%，特征向量较大的是X21，X23。第六主成分方差贡献率最大为5.794%，特征向量较大的是X26，X30。第七主成分方差贡献率最大为4.730%，特征向量较大的是X15。第八主成分方差贡献率最大为4.454%，特征向量较大的是X14，X18。

上述主成分方程分析结果显示特征向量较大 的 为 X4，X11，X14，X15，X16，X17，X18，X19，X21，X22，X23，X26，X28，X29，X30。 我们利用这 15 项主成分特征向量进行下一步聚类分析。

4.2.2 聚类分析过程与结果

（1）聚类分析的过程

利用SPSS软件对十五项标准化的数据进行聚类分析得到下图：

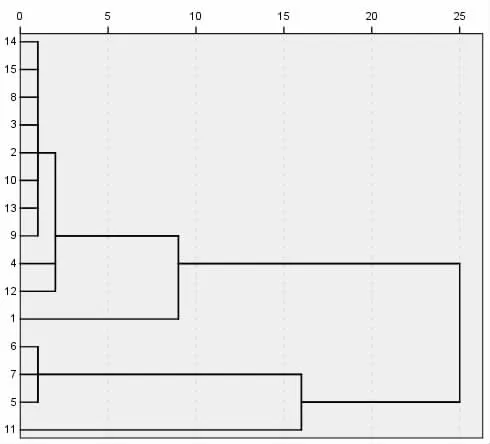
图1 聚类示意图

从图中可以看出14和15的相似度较大，最早聚合为一类， 又与 2、3、8、9、13、10 聚合为一类，4与 12相关系数较大，聚为一类，5、6、7聚为一类，1与11同其他指标差异较大，都单独成为一类，由文献[2-4]可知PH值对葡萄质量的影响较大。

（2）聚类分析的结果

酿酒葡萄的理化性质和葡萄酒的质量与酿酒葡萄有很大关联，故可以以此对酿酒葡萄进行分级，结果如下：

红葡萄：

一级：9、20、23

二级：2、3、4、5、14、17、19、21、22、24、26、27

三级：1、6、10、12、13、16、25

四级：7、8、11、15、18

4.3 问题3的相关性分析及一元、多元回归分析模型

根据第二题中对酿酒葡萄的分级，我们可以用SPSS软件对葡萄酒和葡萄的主要理化指标进行回归及相关性分析，再根据第二问中对主要理化指标的线性分析，分别用Excel作出不同等级酿酒葡萄与葡萄酒理化指标间的典型对比图，由上述我们确定了每一级的酿酒葡萄的突出的理化指标，另外我们也确定了不同等级的酿酒葡萄所对应的葡萄酒样品，通过以上两组数据找出每一级酿酒葡萄所对应的葡萄酒样品理化指标的同异性。这样就可以确定酿酒葡萄与葡萄酒理化指标之间的关系，将其分为三类，分别为线性相关、非线性相关及多元或关系复杂。

4.3.1 葡萄与葡萄酒主要理化指标相关性分析

通过主要理化指标的回归分析， 我们可以得出红葡萄与红葡萄酒理化指标之间的联系。

我们从题设所给的附录2中选出红葡萄与红葡萄酒的主要理化指标，两两之间做回归分析，线性相关的指标为花色苷与花色苷、总酚与总酚、单宁与单宁和白藜芦醇与白藜芦醇等，如总酚与总酚分析为例，如下图：

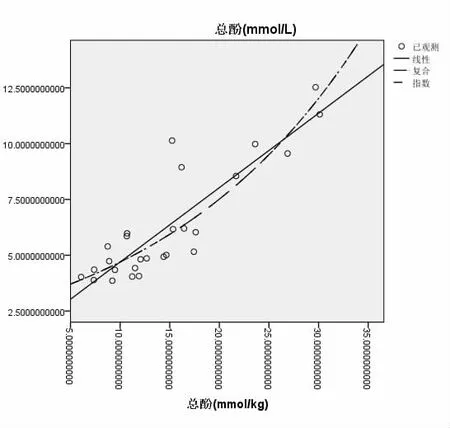
图2 总酚间的关系图

非线性相关的指标为：酒总黄酮与果穗质量，酒总黄酮与黄酮醇，酒总黄酮与白藜芦醇等。

4.3.2 多元回归分析及线性表分析

我们通过SPSS软件对酿酒葡萄与葡萄酒的理化指标进行了多元回归分析，分析后得出，在4.3.1中无法进行归类的一部分理化指标可以归入多元或关系复杂一类中如还原糖与酒总黄酮就属于多元或关系复杂，分析过程及图表略。分析过程中，还原糖被作为复杂因子排除出多元方程，无法与酒总黄酮构成相关，故两者关系多元或关系复杂。

4.3.3 相关结果

我们对酿酒葡萄与葡萄酒的主要理化指标之间的联系进行了分析，通过大量的数据分析以及图表说明，白葡萄用同种方法即可，我们将联系分为三种情况，分别为：

线性相关：如花色苷与花色苷、总酚与总酚、单宁与单宁和白藜芦醇与白藜芦醇。

非线性相关：如酒总黄酮与果穗质量，酒总黄酮与黄酮醇，酒总黄酮与白藜芦醇。

多元关系或关系复杂：如酒总黄酮与还原糖。

4.4 问题4的多元回归模型

4.4.1 相关性分析、多元回归分析

首先对理化指标跟葡萄酒得分的相关性进行分析，从而得出影响得分的主要理化指标。我们对酿酒葡萄及葡萄酒的主要理化指标与葡萄酒质量的之间进行相关性分析来初步判断他们与葡萄酒质量的关系，分析出线性相关的量，由此得出各类主要理化指标与酒质量的相关性关系。

然后利用SPSS对进一步得出的数据进行多元回归分析，得出表4：

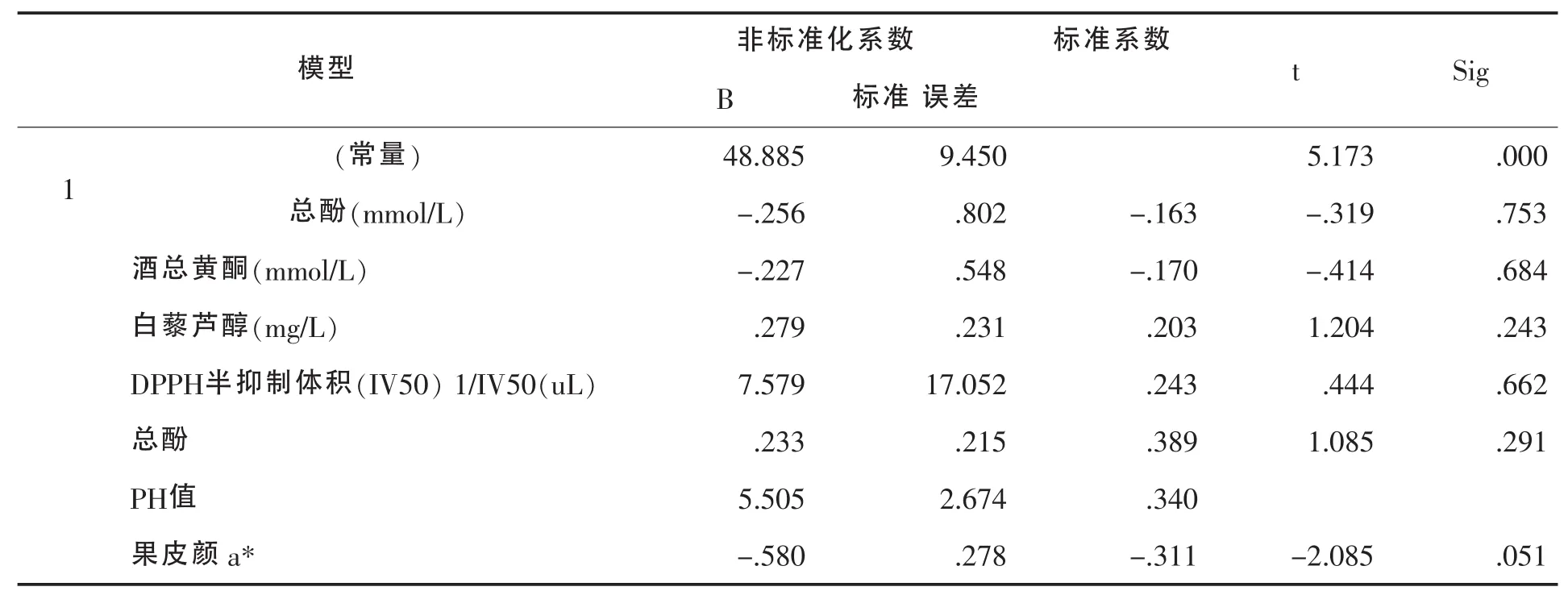
表4 系数a

相应的方程为：

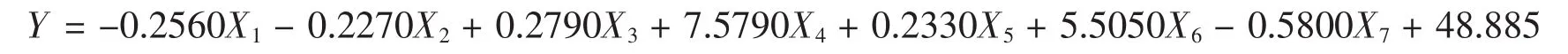
使用Matlab拟合得出图像：

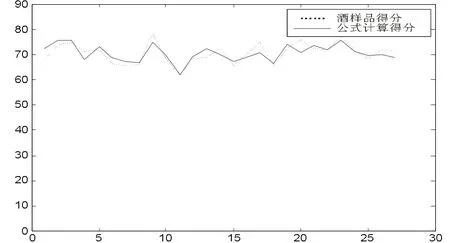
图3 计算公式与实际得分变化趋势比较

由上图显示出利用酿酒葡萄及葡萄酒各项指标做出的公式可以较好的预测实际酒类样品的得分。

4.4.3 考虑芳香类物质对葡萄酒的分的影响

在加入芳香化合物前残差为140.225，加入芳香化合物后残差为135.957，故加入芳香化合物后更加精确。

由以上分析知酿酒葡萄和葡萄酒的理化指标对葡萄酒质量有较大影响，影响程度可以量化，并通过拟合到利用理化指标的计算公式，从而评价葡萄酒的质量。由于实际得分受评酒员水平影响以及葡萄酒的质量还受到制作工艺、催化剂等的影响[6]，通过理化指标计算得分将产生误差，在以上误差分析中可以看到，误差在可接受范围内。

5 模型评价与展望

以上用统计分析等多种方法建立的模型较好地解决了差异性分析，酿酒葡萄等级分类，理化指标联系及葡萄酒得分预测等问题。优点：统计分析、主成分分析、聚类分析等方法成熟，计算可靠，结果直观可信；缺点：各理化指标间的比值对葡萄酒产生的影响使得非线性因素增加，导致问题变复杂，产生误差。可以考虑进一步将典型理化指标的比值作为新的指标考虑，这样有利于增加模型结果的精确程度。

[1]http://www.mcm.edu.cn/,访问时间：2012年11月3日（A题及数据来源）.

[2]马腾，赵丽，李军.2008年份昌黎原产地葡萄酒理化特性的统计学分析[J].河北科技师范学院学报，2012，26（1）:5-11.

[3]吴桂芳，蒋益虹，王艳艳，等.基于独立主成分和BP神经网络的干红葡萄酒品种的鉴别[J］.光谱学与光谱学分析，2009，29（5）:268-271.

[4]中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会.GB/T 15038-2006葡萄酒、果酒通用分析方法[S].北京:中国标准出版社，2008.

[5]李华，刘永强，郭安鹊，等.运用多元统计分析确定葡萄酒感官特性的描述符[J].中国食品学报，2007,（4）:114-11.

[6]秦含章.葡萄酒分析化学[M].北京:中国轻工业工业出版社，1991.