提高ANSYS中BEAM188梁单元计算精度的方法

刘玉卿，陈孝建，杨树耕，汪 睿，刘小燕

（天津大学，天津300072） ①

提高ANSYS中BEAM188梁单元计算精度的方法

刘玉卿，陈孝建，杨树耕，汪 睿，刘小燕

（天津大学，天津300072）①

BEAM188单元沿梁长度方向的弯矩为阶梯状分布，与理论分析结果存在较大误差，对计算精度有很大影响。为提高计算精度，提出了采用二次型的BEAM188单元的方案，并通过计算检验了二次型梁单元的收敛速度和计算精度。结果表明，该方案能够在保证计算效率的前提下显著地提高计算精度。

海洋平台；BEAM188；二次型；高斯积分点

在海洋工程中，大型有限元通用软件ANSYS有着广泛的应用［1－2］。在海洋平台上部模块的板梁组合结构的计算过程中，骨材通常用ANSYS中的BEAM188单元模拟。BEAM188单元在计算时采用默认的设置，此时单元沿梁长方向采用了1个高斯积分点［3］，为三维线性单元。

由于线性单元的局限性，计算结果有较大误差。例如，在计算跨中承受集中载荷的两端铰支的单跨梁时，理论上沿梁长方向的弯矩为三角形分布，如图1所示；而在默认的情况下，BEAM188单元计算得到的弯矩为阶梯状分布，与力学理论值误差很大，如图2所示。在弯距分布图中，与本文计算结果有关的为：MYI和MYJ表示I和J节点的y轴弯矩，MIN和MAX表示最大和最小的弯矩，ELEM表示相应的单元编号。本文仅把弯矩数值列于表中，而不在图中表示。

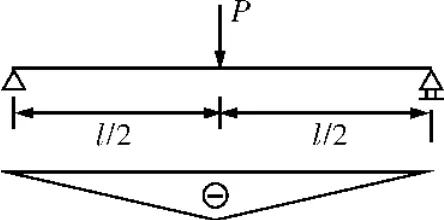
图1 力学模型及力学解

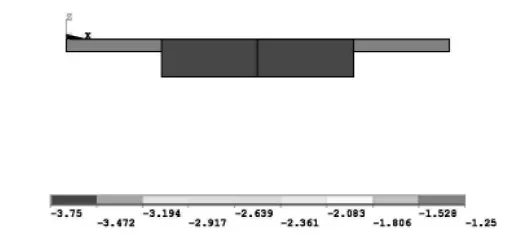
图2 BEAM188单元弯矩分布图

在有限元计算中，为了提高计算精度，通常采取细化网格的方法［4］。但是，对于复杂模型，例如海洋平台的主船体结构，细化网格会直接导致计算量成倍增加，降低计算效率。有时在网格过密时，甚至会导致计算无法进行。

为了在保证计算效率的情况下提高计算精度，本文建议采用二次型的梁单元进行计算，可以有效地提高计算精度。

1 BEAM188单元介绍

BEAM188梁单元是工程计算中常用的单元类型，适合于分析从细长到中等粗短的梁结构。该单元基于铁木辛哥梁结构理论，并考虑了剪切变形的影响，是三维线性有限应变梁单元［5－6］。

在默认的KEYOPT（3）＝0设置时，BEAM188单元为一阶铁木辛哥梁单元，沿着梁长方向采用了1个高斯积分点进行计算，如图3所示。

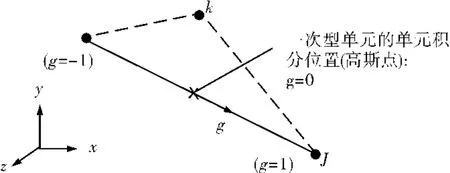
图3 一次型梁单元高斯积分点示意

将BEAM188单元的KEYOPT（3）选项设置为2时，BEAM188为二次型梁单元。二次型单元运用中间节点（中间节点用户无法修改）提高单元的计算精度。在计算内力时，沿着梁长方向采用两2个高斯积分点进行计算，得到2个高斯点上的内力，然后将这2个点上的内力进行线性外推，得到单元节点上的节点力，如图4所示。这种方法能够精确地计算线性变化的弯距，而且对于非线性变化的弯矩，也要比一次型梁单元的计算精度高。

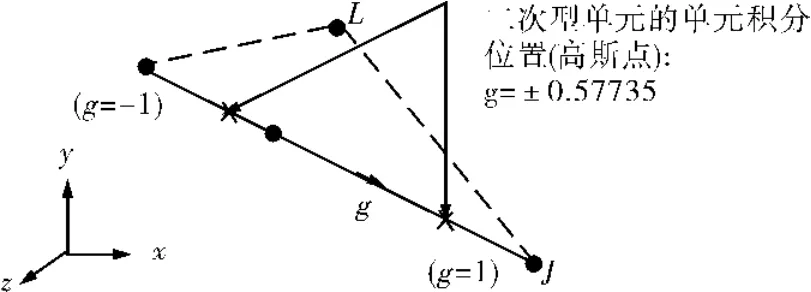
图4 二次型梁单元高斯积分点示意

2 二次型在单跨梁结构中的应用

前面分别介绍了一次型和二次型的BEAM188梁单元，现在通过简单的单跨梁结构分析比较两者在计算精度方面的差异。

建模时，梁截面为T型钢（300×8＋150×12），截面惯性矩为0.384×10－4m4，杨氏模量E＝2.0× 108kN／m2，泊松比μ＝0.3。

2.1 两端刚性固定承受集中载荷的单跨梁

承受集中载荷的单跨梁沿梁长方向的弯矩呈线性分布。力学模型如图5，弯矩分布如图6～7，计算数据如表1。通过对比一次型和二次型的计算结果可知：

1） 一次型梁单元计算得到的弯矩呈阶梯状分布，与力学理论解有很大误差。

2） 提高一次型的网格密度，可以提高计算的精确度。

3） 在相同的网格划分情况下，二次型的计算结果明显要比一次型的精确。

4） 二次型可以很准确地模拟线性变化的弯矩分布，与理论值无误差。

5） 二次型的计算精度与网格密度无关，但是将梁的整体作为1个分段的情况除外。

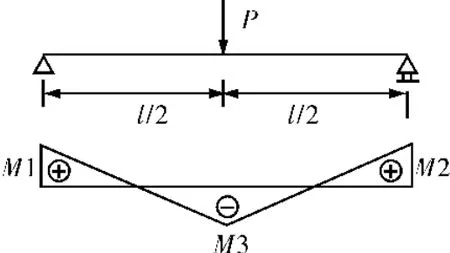
图5 集中载荷刚固梁力学模型

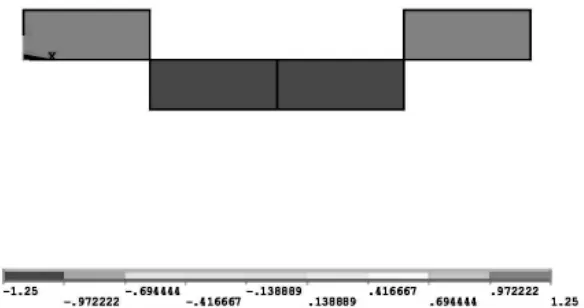
图6 集中载荷刚固梁一次型弯矩分布

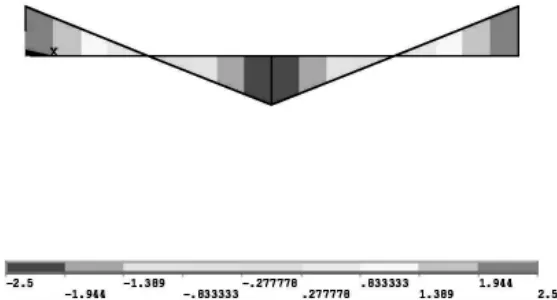
图7 集中载荷刚固梁二次型弯矩分布

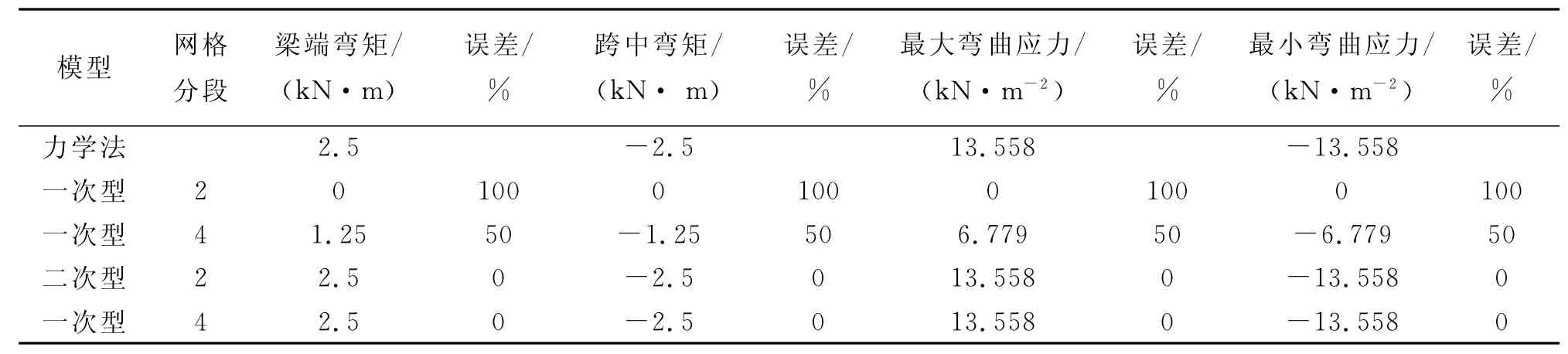
表1 刚性固定单跨梁在集中载荷作用下的计算结果

2.2 两端刚性固定承受均布载荷的单跨梁

该力学模型中，沿梁长度方向的弯矩为非线性约束，且弯矩有正也有负，分布于轴线两侧。力学模型如图8，弯矩分布如图9～10，计算数据如表2。

对于弯矩为非线性变化的简支梁结构，通过对比一次型和二次型的计算结果可知：

1） 一次型的弯矩呈阶梯状分布，与力学理论解有很大误差。

2） 在网格划分相同的情况下，二次型比一次型更加准确。

3） 提高网格的密度，可以提高计算的精确度，且二次型的计算结果比一次型更快地趋近于理论值。

通过综合比较BEAM188单元在单跨梁结构计算中的结果可以看出：在收敛速度方面，二次型可以更快地收敛于理论值；在准确度方面，二次型比一次性相对误差小，尤其在模拟承受集中载荷作用的梁（即弯矩沿轴长方向线性分布）方面，弯矩分布情况和理论解相同，可以得到精确解。

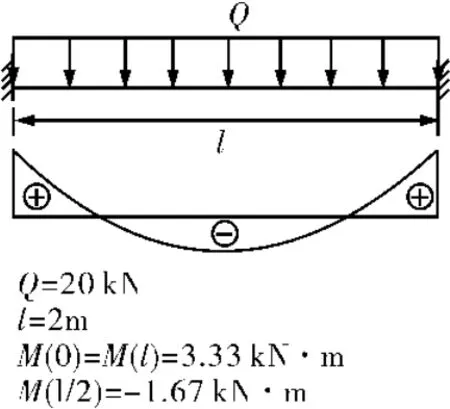
图8 均布载荷刚固梁力学模型

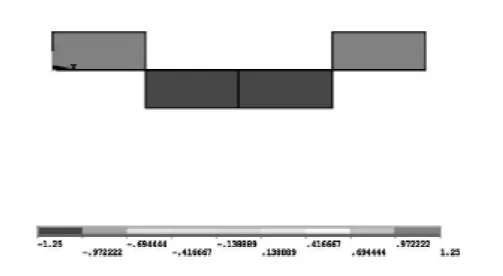
图9 均布载荷刚固梁一次型弯矩分布

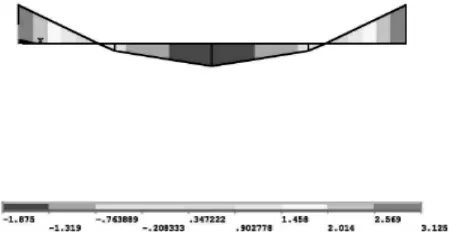
图10 均布载荷刚固梁二次型弯矩分布

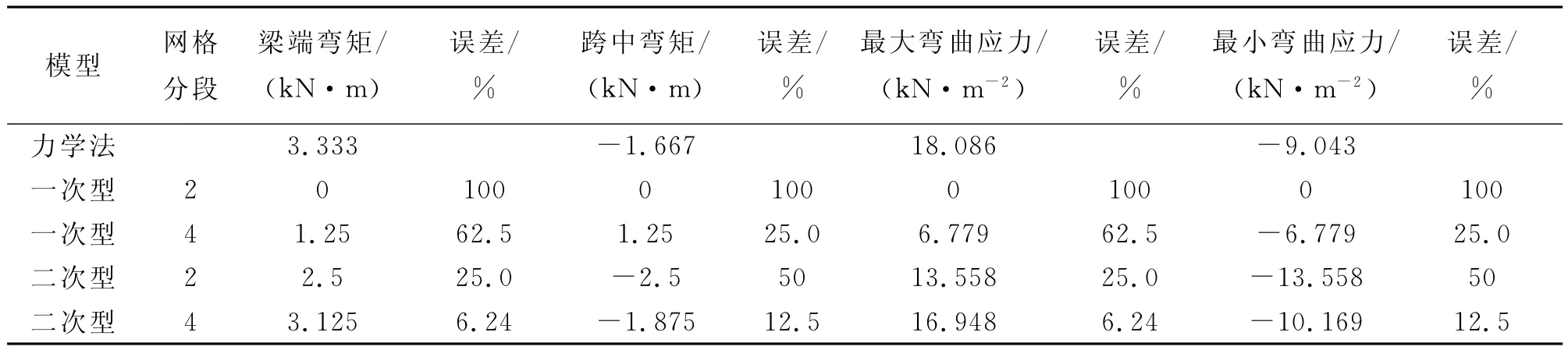
表2 刚性固定单跨梁在均布载荷作用下的计算结果

3 二次型在板梁组合结构中的应用

海洋工程结构物的设计和建造，讨论的对象主要是承受垂直于板平面载荷的、具有不同边界条件的板梁结构，考虑的主要是板和梁的弯曲变形问题。板梁组合结构的模拟计算中，梁（即骨材）通常用BEAM188单元模拟。

前面讨论了BEAM188单元在单跨梁结构中的应用，下面比较一次型和二次型的梁单元在板梁组合结构中的精确度。

3.1 四边自由支撑的板架结构

四边自由支撑的横骨架式矩形板架结构如图11，边长8m。桁材为T型钢（600×12＋200×18），惯性矩I＝0.411×10－3m4；骨材为角钢（150× 90×9），惯性矩I＝0.489×10－5m4；板厚8mm。求均布载荷q＝10kN／m2作用下桁材和骨材的弯矩分布（E＝2.0×108kN／m2，μ＝0.3）。

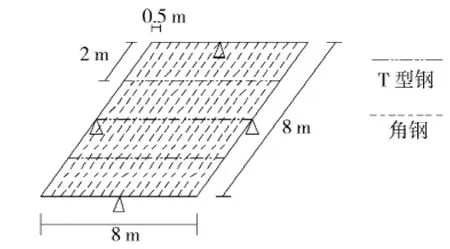
图11 四边自由支撑的板架结构

在ANSYS建模时，将桁材和骨材统一设置成一次型或二次型进行求解计算，以分析比较桁材和骨材在一次型或二次型情况下的收敛速度和计算精度。

在建模时不考虑梁单元的偏移，即认为桁材和骨材横截面的形心在板材的中线面处。

分析得出，板梁组合结构中间位置处的桁材和骨材上的弯矩值相对较大。现在以中间位置处的桁材和骨材上的弯矩分布进行分析比较，如表3～4。

在表3～4中，网格划分指板格上每一边的划分段数。

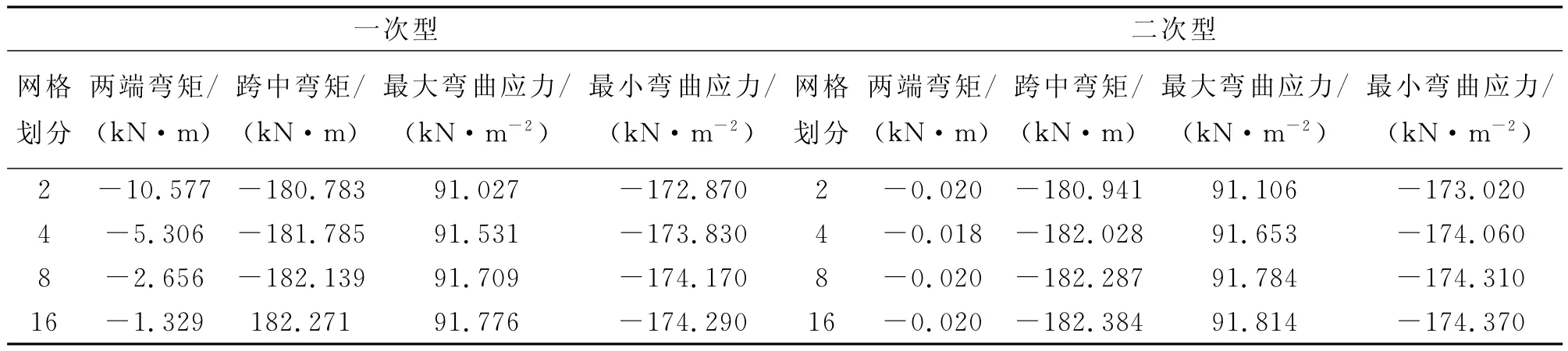
表3 四边自由支撑的板架中间位置桁材弯矩计算结果

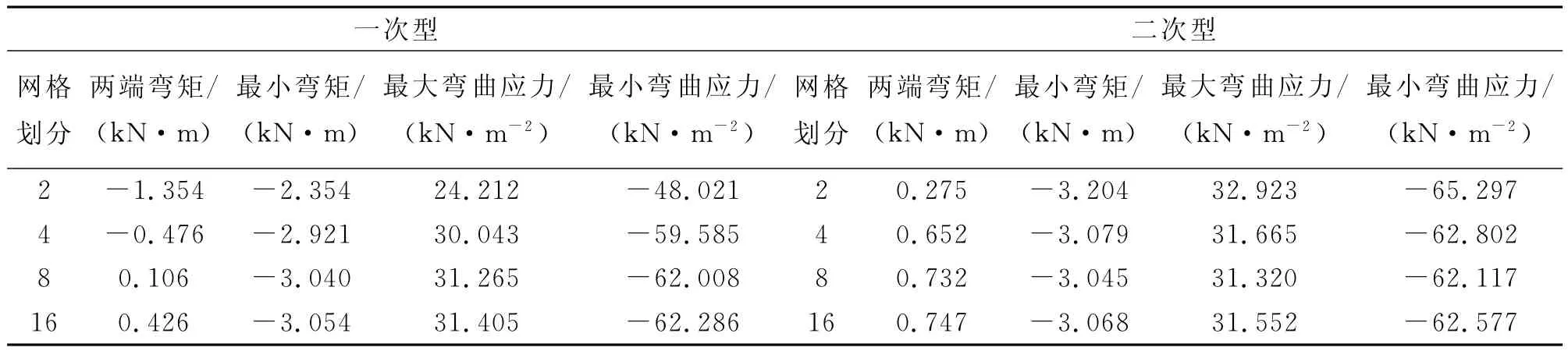
表4 四边自由支撑的板架中间位置骨材弯矩计算结果

3.2 四边刚性固定板架结构

以四周刚性固定的矩形板架为例，分析比较一次型和二次型的计算结果。模型的四周边界为刚性固定，其余条件均与第3.1节相同，不再赘述。计算结果如表5～6。

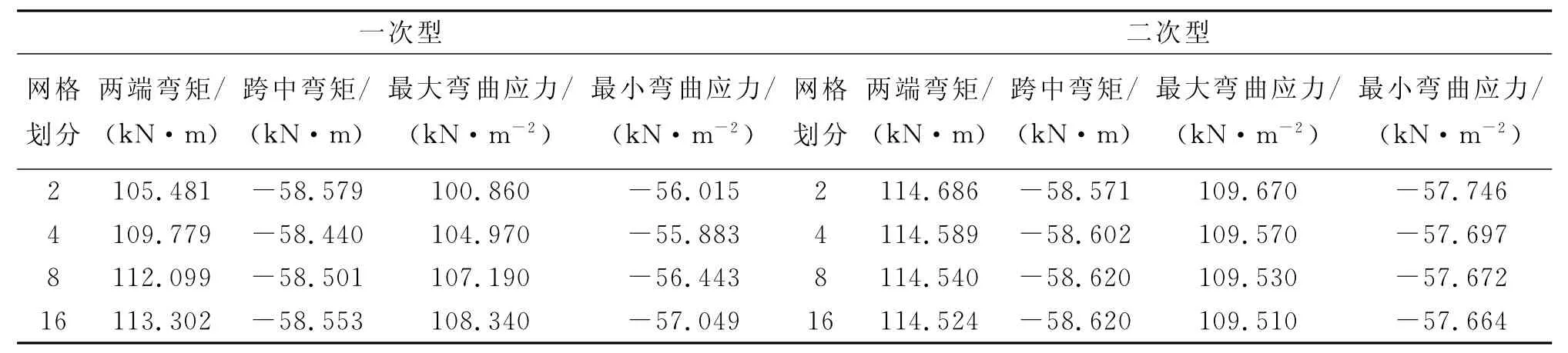
表5 四边刚性固定板架中间位置桁材弯矩计算结果

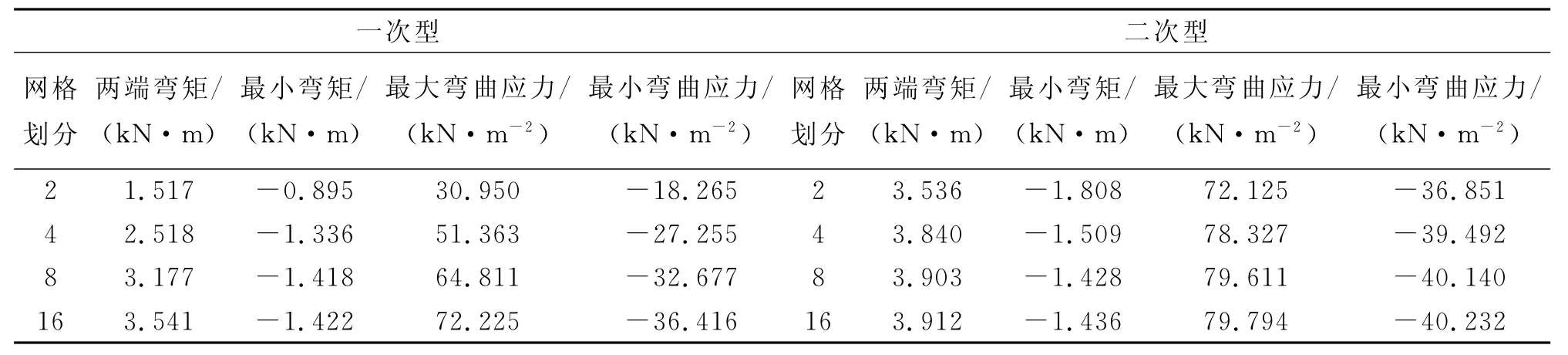
表6 四边刚性固定板架中间位置骨材弯矩计算结果

根据有限元原理可知，网格划分越密集，计算结果越准确［7－9］。由于板架结构不易求得力学精确解，可认为在网格划分足够密集的情况下，其结果趋近于精确解，并以其作为精确度的比较判断标准。

综合分析以上2种约束情况下的板梁结构的计算数据，可知：

1） 细化网格，可以提高计算精度。

2） 网格划分越密集，计算结果越精确，但是同时计算量也大。

3） 桁材为板架结构中的强构件，计算结果收敛较快。

4） 骨材的计算结果收敛较慢。

5） 板架结构的计算中，二次型在收敛速度和计算精度方面要明显优于一次型。

实际的海洋工程结构物，例如主船体的甲板或舱壁板，均为板架组合结构。其边界条件介于自由支持和刚性固定之间。从以上结果数据的趋势可以看出，无论是四周自由支持，还是四周刚性固定，二次型在收敛速度和计算精度方面都要优于一次型的BEAM188单元。由此可以推断，对于介于上述2种边界条件之间的约束情况，二次型的BEAM188梁单元也要比一次型精确。

3.3 建议

在相同情况下，二次型BEAM188单元的计算精度比一次型高，但是由于计算量大，计算速度比较慢。为了在提高精度的同时保证计算效率，对于复杂结构，建议将重要部位的梁或骨材采用二次型的BEAM188单元模拟，将一般部位的梁构件采用一次型进行模拟，这样可以在提高计算精度的同时保证计算效率。

4 结论

1） 在有限元计算中，提高网格密度，可以提高计算精度。

2） 在相同的网格划分情况下，二次型的BEAM188单元在收敛速度和计算精度方面要明显优于一次型的BEAM188单元。

3） 在结构中综合运用一次型和二次型的BEAM188单元，可以在保证计算效率的情况下提高计算精度。

4） 本文以单跨梁和板梁结构为例，分析比较了一次型和二次型的BEAM188梁单元在结构计算中的收敛速度和计算精度，并得出了结论。这对提高ANSYS在结构有限元分析计算中的精度和效率具有重大意义。

［1］ 杨树耕，孟昭瑛，任贵永.有限元分析软件ANSYS在海洋工程中的应用［J］.中国海洋平台，2000，15（2）：41－44.

［2］ 孙志娟，孟庆鑫，周 到.海洋石油平台水下夹桩器本体结构分析［J］.石油矿场机械，2007，36（1），36－38.

［3］ 王勖成.有限单元法［M］.北京：清华大学出版社，2003：80－100.

［4］ 陈铁云，陈伯真.船舶结构力学［M］.上海：上海交通大学出版社，1991：163－195.

［5］ Simo J C，Vu－Quoc L.A Three Dimensional Finite Strain Rod Model.PartⅡ：Computational Aspects［J］.Computer Methods in Applied Mechanics and Engineering，1986，58：79－116.

［6］ Ibrahimbegovic，Adnan.On Finite Element Implementation of Geometrically Nonlinear Reissner＇s Beam Theory：Three－dimensional Curved Beam Elements［J］.Computer Methods in Applied Mechanics and Engineering 1995，122：11－26.

［7］ 江见鲸，何放龙.有限元法及其应用［M］.北京：机械工业出版社，2007.

［8］ S·铁木辛哥，J·盖尔.材料力学［M］.胡人礼，译.北京：科学出版社，1987.

［9］ 李 妍，吴艳新，高德利.深水钻井隔水管纵横弯曲变形解析［J］.石油矿场机械，2011，40（9）：21－24.

Study and Improving Accuracy of ANSYS BEAM188Element in Structure Calculation

LIU Yu－qing，CHEN Xiao－jian，YANG Shu－geng，WANG Rui，LIU Xiao－yan
（Tianjin University，Tianjin300072，China）

There is a big error in the bending moment distribution along the beam between the theoretical value and BEAM188element calculation results.In order to improve accuracy，aquadratic BEAM188element is a better choice.The result shows that this method can improve the calculation accuracy in the premise of ensuring computational efficiency.

marine platform；BEAM188；quadratic；Gauss integral point

1001－3482（2012）04－0039－05

TE95

A

2011－10－28

刘玉卿（1986－），男，河北石家庄人，硕士研究生，主要从事船舶与海洋工程结构物的设计与建造工作，E－mail：yqliu＿tju＠yahoo.com.cn。