直流潮流概述及其在灵敏度分析中的应用

刘超男 刘昌卿

1.国网技术学院 山东 济南 250002；2.华能日照电厂 山东 日照 276826

0 引言

电力系统潮流计算是电力系统运行分析的一项基本计算，可以通过多种方法来实现，如牛顿法、P－Q分解法、保留非线性算法等［1－2］，这些方法都属于精确的交流潮流计算，所采用的数学模型和得到的计算结果都有很好的精确度，但需要进行多次迭代运算，计算量较大、耗费的时间较多。在有些情况下，如系统规划设计时，原始数据并不很精确且规划方案很多；或在实时安全分析中，要进行大量的预想事故筛选等。这些场合对计算速度的要求比对计算精确度的要求更高。因此采用近似模型的直流潮流算法可有效地减少计算量，大大地提高了计算速度［3－4］。

文献［3］在直流潮流计算中考虑了高压输电网络中的不确定性因素，并采用区间分析方法进行处理，可应用于求解大规模输电系统。文献［5］基于直流潮流的简化模型，研究了风电功率在静态安全约束下的传输功率能力。文献［6］给出一种基于直流潮流灵敏度的断面潮流定向控制新方法。利用直流潮流获得断面支路对应的发电机输出功率转移分布因子矩阵，进而根据断面潮流定向控制需要，通过非线性优化确定断面潮流调控方案。文献［7］通过分析西部地区电网的网络拓扑结构，结合高压线路特点，运用直流潮流法对电网进行可靠性评估。

本文通过分析直流潮流计算的特点和相应的原理，基于matlab平台编写了相应的程序；通过算例分析对直流潮流与交流潮流计算进行了对比；最后深入分析了直流潮流在灵敏度计算中的应用，通过直流潮流计算发电转移分布因子（GSF）与线路开断分布因子（LODF），进而分析发电机功率变化以及线路开断对系统的影响。

1 直流潮流的原理

直流潮流算法［8－10］主要具有以下两个优点：

1）计算快，内存占用量少，同时也有足够的精度，尤其是对于高压或超高压电网，计算表明其误差一般不超过3～5%。

2）由于直流法中不需要迭代的线性关系，使得它在计算断线后的潮流分布上表现出极大的优越性，特别适合于N－1线路安全分析。

直流潮流模型是在交流潮流模型基础上经过简化导出得到的，如图1所示，交流网络中某条支路i－j中所通过功率的表达式为：

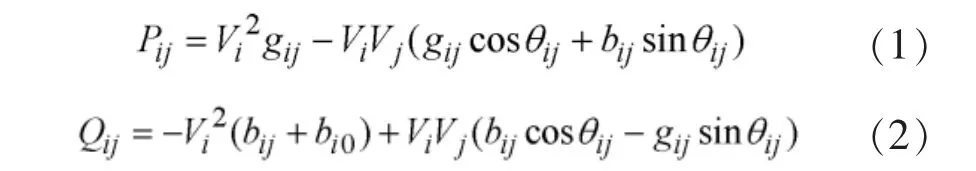
式中，Pij，Qij为支路的有功和无功潮流，Vi为节点i的电压幅值。

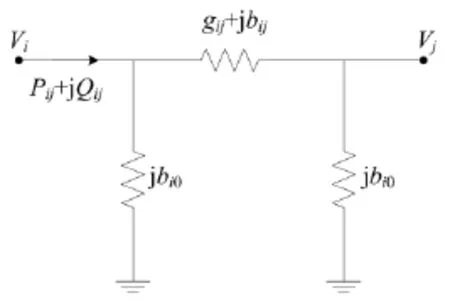
图1 单条线路的等值电路图

在直流法潮流计算中，采用以下假设：

1）高压输电线路的电阻远小于电抗，故忽略线路电阻，则支路电纳为bij＝－1／xij，其中xij为不接地支路的电抗。

2）输电线路两端电压相角差不大，可以认为cosθij≈1，sinθij≈θij。

3）假定系统中各节点电压标幺值都等于1，即Vi≈Vj＝1.0。

4）不计接地支路的影响，即bi0＝0。

由此，式（1）和式（2）可近似简化成：

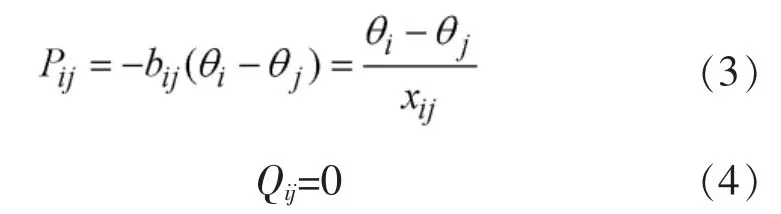
忽略支路的无功潮流后，由式（3）可知相应的交流支路可看成是一条直流支路，其两端相应的直流电压值分别为θi及θj，直流电阻等于支路电抗xij，直流电流值为相应的有功功率Pij。

对于n个节点的系统，设定平衡节点s的相角θs＝0°，根据节点功率等于与节点相连的支路功率之和，即

可得：

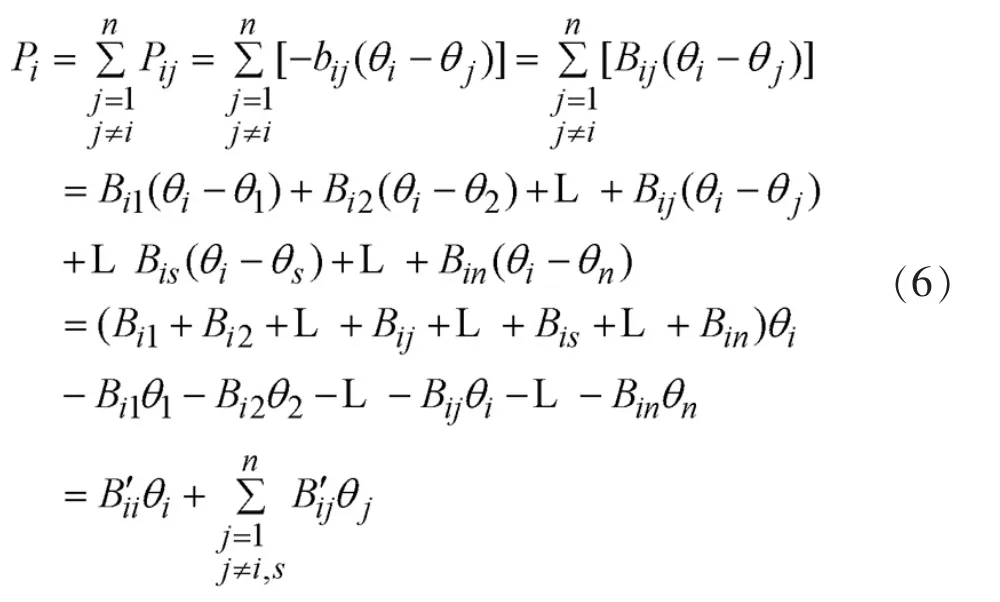
其中，

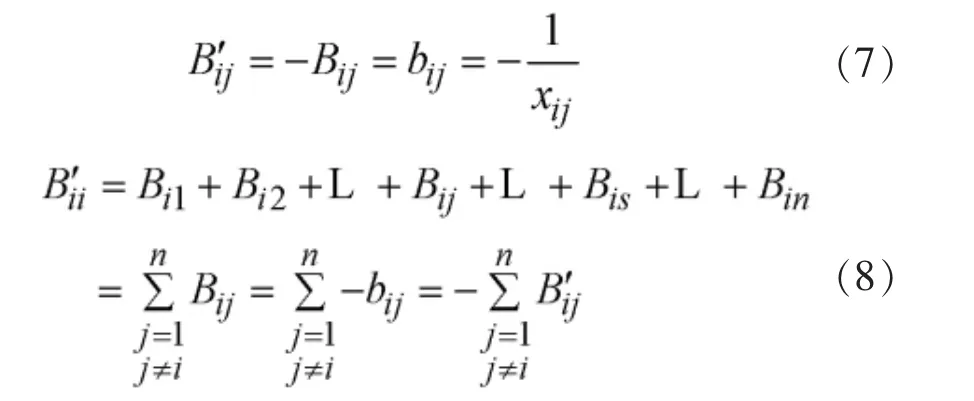
式中，Bii′和B′分别为以1 ／xij为支路导纳建立起来的节点导纳矩阵的自导纳及互导纳。

除了平衡节点s外，其余n－1个节点的方程若写成矩阵形式，即得到n节点电力系统的直流潮流数学模型。

式中，P和θ分别为n－1阶节点有功功率注入和电压相角向量，其中不包括作为角度参考点的平衡节点的有关量。不难看出，式（9）是一个线性方程组，可以一次直接求解得到结果，因而计算速度非常快。

2 直流潮流与交流潮流的对比

实际应用中，直流潮流常被用于电力系统安全分析，电网输电阻塞调度等领域，这一方面是由于直流潮流计算速度快，占用内存少，且是线性方程组，更重要的在于直流潮流的精度有一定的保证，下面采用IEEE 3机9节点系统来测试直流近似潮流与交流精确潮流的结果差异，如图2所示。

基于matlab平台实现了直流潮流相应的计算程序，通过仿真计算可得各支路功率和节点电压相角，与IEEE测试系统所给结果进行对比如表1，表2所示。其中相对误差的计算如下所示：

图2 IEEE3机9节点系统接线图

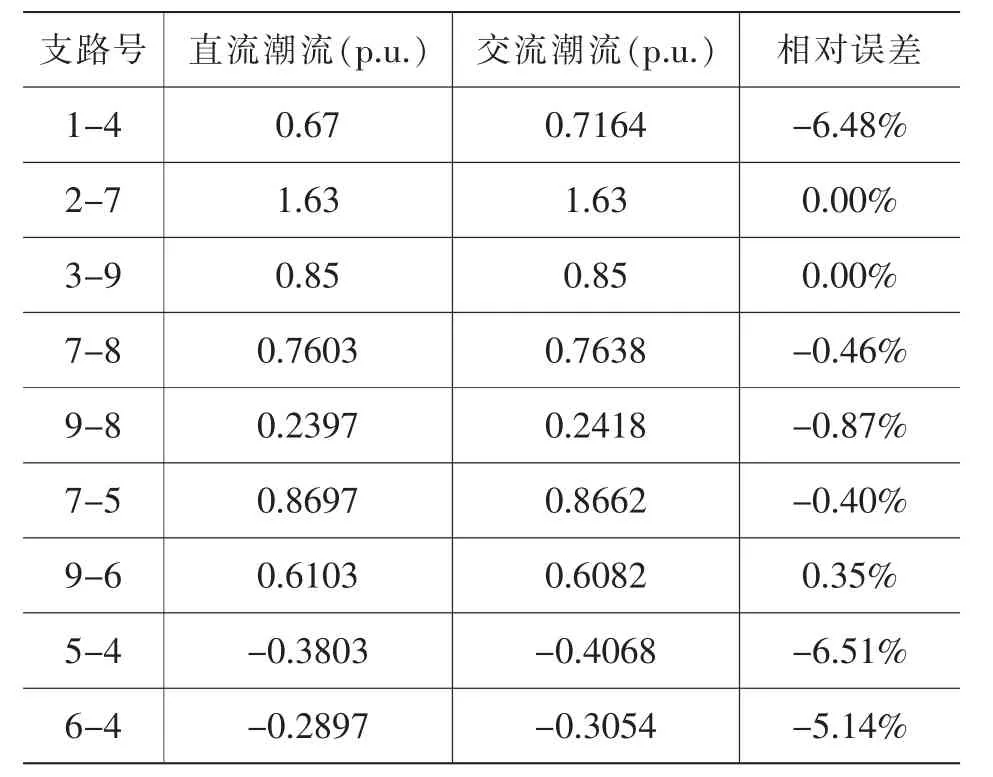
表1 支路潮流结果对比

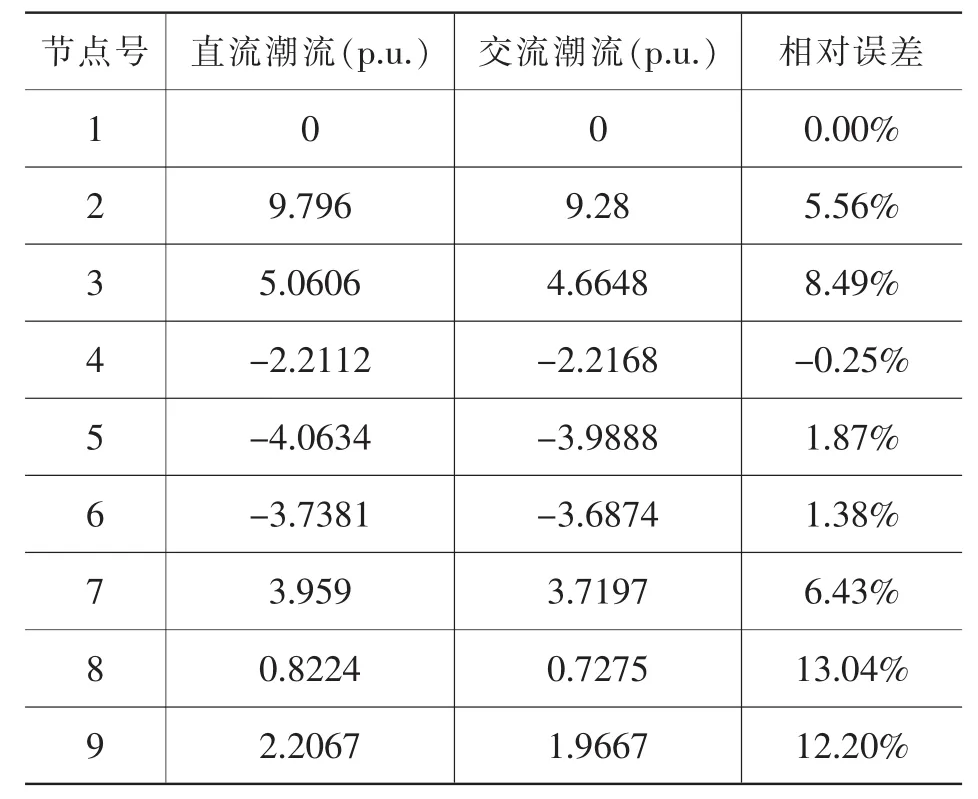
表2 节点电压相角结果对比

由表1和表2可以看出，由于采用直流潮流法计算时采用了给定的假设条件，如忽略线路损耗及无功的影响，使得所得结果与交流潮流的精确解有一定的差异。另外，由结果可知，远离平衡节点处（8，9，3，7，2）的电压相角误差较大，都在5%以上；而靠近平衡节点处的支路（1－4，5－4，6－4）的功率误差较大，也都达到5%以上。这是由于直流法假定电网中各处的电压幅值都为1.0。

3 元件开断对系统的影响

由于直流潮流是线性方程组，因而可以较方便地计算元件开断对系统的影响，特别是多重支路开断的影响。本文通过发电转移分布因子与线路开断分布因子来分析发电机功率变化以及线路开断对系统的影响。

3.1 各种分布因子的定义

将式（3）代入式（9）可得：

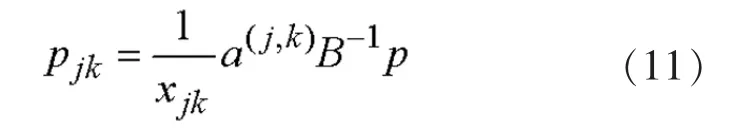
式中，a（j，k）是对应jk的支路节点关联行向量，该向量仅在第j位置为1，在第k位置为－1，其余位置元素均为0。

发电转移分布因子可以描述为：

式中：Δpjk表示第jk支路在节点i发电功率变化为Δpi时支路潮流的变化。

根据式（12），令式（11）中的向量p仅在第i个位置为1，其余为0，则：

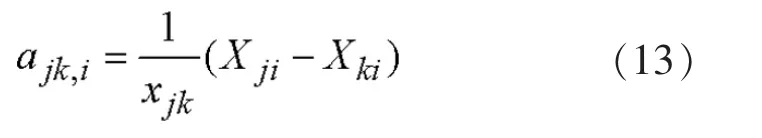
式中：Xji、Xki为节点电抗阵中i行（列）的第j和第k个元素。

线路开断分布因子可以定义为：

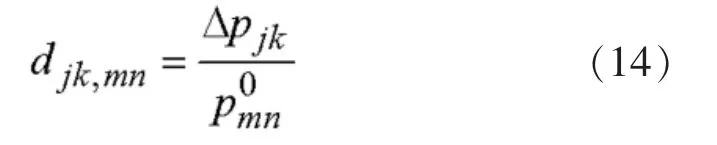
根据式（14）的定义，线路开断分布因子可以通过如下等效注入法求出。

支路mn开断等效注入表示为：

式中，Δpm和Δpn为节点等效注入，Δpmn和Δpnm为节点注入引起支路潮流的变化。由此支路电压变化为：

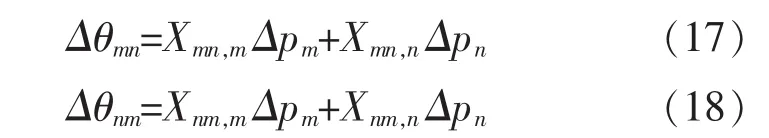
式中：Xmn，m为仅在m节点注入单位电流引起支路电压的变化的贡献系数，该系数来自节点电抗阵的相关元素。

同时，支路潮流变化可以表示为：

将式（17）和（18）分别代入（19）和（20）有：

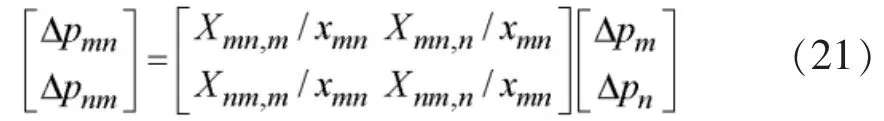
结合式（19）和（20），有：

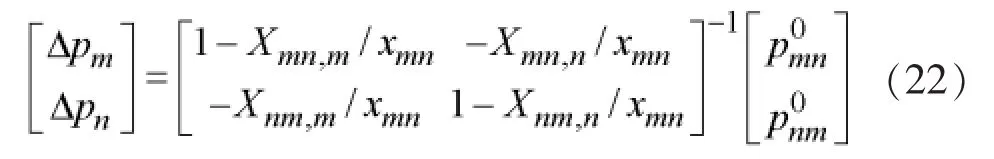
由上式等效注入可求出各节点的电压变化，尽而求出支路潮流的变化，与开断前迭加即可求出开断后各支路潮流的值。同时根据（14）可以求出线路开断分布因子。

3.2 算例分析

依据前述，编程计算IEEE 3机9节点系统的发电转移分布因子和线路开断分布因子分别如表3和表4所示。

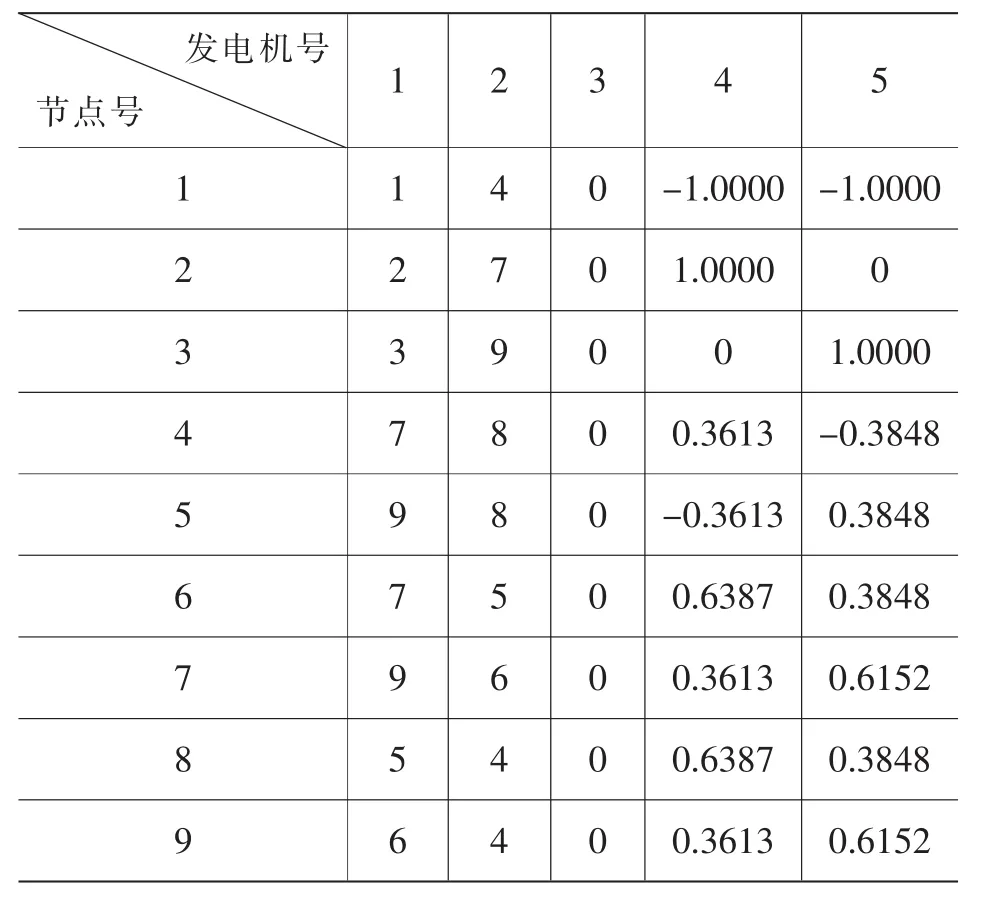
表3 发电转移分布因子

因为假设某发电机断开后，其功率全部由平衡节点处发电机承担，因此由表3可以看出，2号发电机断开后，1－4支路的功率增加量即为2号机的功率，除此线路外，线路4－5－7功率增加最大。3号发电机断开后，也由平衡节点承担，1－4支路功率增加量为3号机的功率，除此线路外线路4－6－9功率增加较多。

4 总结

直流潮流模型是在交流潮流模型基础上经过简化导出得到的，采用了一定的合理的假设，使得电力系统潮流计算大为简化，计算时间缩短，占用内存量减少。同时，其线性的特性也使得直流潮流在安全分析等领域得以应用。

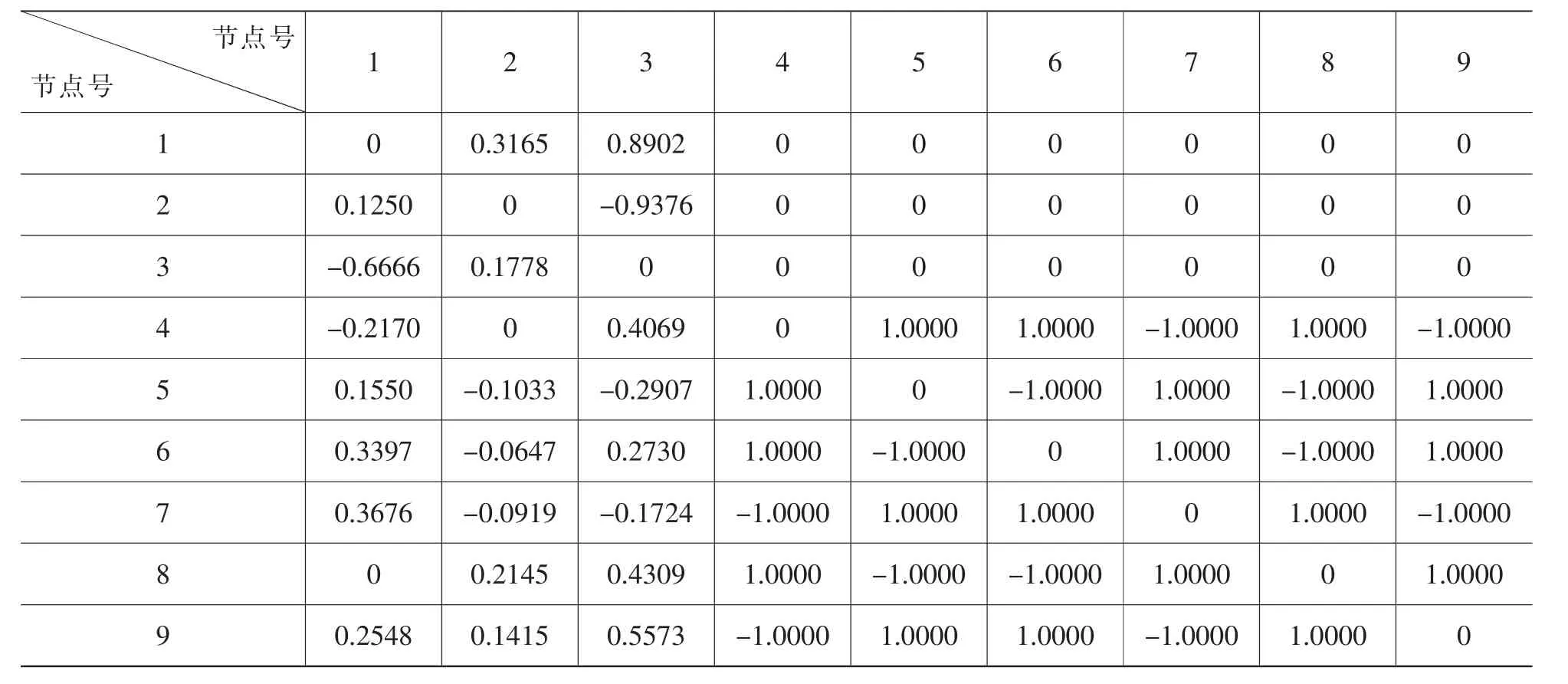
表4 线路开断分布因子

本文以IEEE 3机9节点系统为测试系统，分别采用直流潮流法与交流潮流法计算，并对结果进行了对比。由于直流潮流的假设条件在特高压系统中才能得到更好的满足，因此，在本测试系统中，两种方法的结果差异较大，支路功率差异最大达到13%，节点电压相角差异最大达到6%。这也说明了直流潮流虽然有许多优点，但其使用也有一定的局限性，要依据实际需要进行选择。另外，采用直流潮流灵敏度分析法对该系统进行了分析，分别考虑了发电机开断以及线路开断对系统的影响。其中，发电机开断时，其功率全部由平衡节点承担；线路有开断时，节点功率通过环网传递。这两类故障发生后，对系统的冲击都比较大，系统安全受到影响。

［1］诸骏伟.电力系统分析（上册）［M］.北京：水利电力出版社，1995.

［2］王守相，刘玉田.电力系统潮流计算研究现状［J］.山东电力技术，1996，（5）：8－12.

［3］王守相，武志峰，王成山.计及不确定性的电力系统直流潮流的区间算法［J］.电力系统自动化，2007，31（5）：18－22.

［4］叶剑，陶玉华.一种基于直流法潮流的快速潮流计算方法［J］.华北电力技术，2010，（5）：7－10.

［5］马乐，颜湘武，刘艳萍.基于直流潮流计算的风电接入能力分析［J］.电网与清洁能源，2010，26（10）：50－52.

［6］贾宏杰，穆云飞，余晓丹.基于直流潮流灵敏度的断面潮流定向控制［J］.电力系统自动化，2010，34（2）：34－38.

［7］许自纲，王洪，秦晓平.直流潮流法在西部电网可靠性评估中的应用［J］.电力科学与工程，2009，25（7）：31－33.

［8］张伯明，陈寿孙.高等电力网络分析［M］.北京：清华大学出版社，1996.

［9］王锡凡，方万良，杜正春.现代电力系统分析［M］.北京：科学出版社，2003.

［10］邹森.电力系统安全分析与控制［M］.北京：水利电力出版社，1995.