一种基于改进混合蛙跳的聚类算法*

韩晓慧，王联国

(1.甘肃农业大学工学院，甘肃兰州730070;2.甘肃农业大学信息科学技术学院，甘肃兰州730070)

0 引言

聚类分析［1］作为数据挖掘在实际应用中的主要任务之一，是数据挖掘领域中一个很活跃的研究课题。近几十年来得到了快速发展和成功应用。所谓聚类就是按照某个特定标准(一般为距离准则)把一个数据集分割成不同的类或簇，使得在类内的数据点的相似性尽可能大，同时类间的数据点的差异性也尽可能大［2］。

目前聚类算法主要分为:划分聚类、层次聚类、基于网格的聚类和基于密度的聚类。K—均值算法作为划分聚类中最经典的聚类算法之一，但它是一个局部搜索的算法，存在一些严重不足［3］:K值需要预先确定;聚类结果的好坏依赖于初始簇中心点的选取等。为此，许多研究者提出了基于智能优化算法的聚类方法［4～6］。

混合蛙跳算法作为智能算法的一种优化算法，是2000年由Eusuff和Lanse通过类比青蛙的觅食行为与优化问题求解的相似性而提出了一种新的基于全局协同搜索的智能优化方法。由于具有概念简单、参数少、求解快速等诸多优点已被应用于许多自然科学与工程科学领域，显示出强大的优势和潜力。对求解实优化问题，大量实验已证实，混合蛙跳算法较遗传算法收敛速度快、效率高。鉴于此，本文在文献［7］讨论改进混合蛙跳算法的基础上，提出了一种新的改进混合蛙跳的聚类算法，对算法进行了实验分析，并与基于传统混合蛙跳聚类算法、基于遗传聚类算法和基于蚁群聚类算法进行了比较，仿真实验证明本文提出的算法性能优于这几种算法。

1 K—均值聚类算法

K—均值算法是一种基于划分的方法，假设给定有n个对象的数据库和聚类数目K。一个划分方法构建数据的K个划分(K≤n)，每一个划分代表一个聚类。聚类依据对象之间的相似度函数，通常用距离来衡量，而距离度量的方式有很多，对于RN空间中的向量，最直观的距离度量是向量之间的欧氏距离d=‖x－z‖。聚类的结果是达到类间的对象尽可能不同，类内的对象尽可能相似。

K均值聚类算法的过程描述如下:

输入:数据集 X=(x1，x2，…，xn)，聚类数目 K

输出:K个簇Cj

K—均值算法步骤描述如下:

1)从{x1，x2，…，xn}中随机选取K个数据对作为初始簇(聚类)中心 z1，z2，…，zk;

2)计算每一个数据点xi，i=1，2，…，n与这K个簇中心Cj，j∈{1，2，…，k}的距离，如果满足‖xi－zj‖＜‖xi－zm‖，m=1，2，…K，m≠j则 xi∈Cj

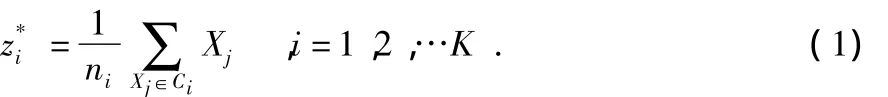
为防止不能满足步骤(4)的终止条件出现无限循环，一般在算法执行时给一个固定最大迭代次数。

2 混合蛙跳算法

2.1 传统混合蛙跳算法

混合蛙跳算法(SFLA)是一种受自然生物模仿启示而产生的基于群体的协同搜索方法。在SFLA中，青蛙群体(解集)由一群具有相同结构的青蛙(解)组成，整个群体被分为多个子群，每个子群有自己的文化，执行局部搜索策略。子群中的青蛙均具有自己的思想，在局部搜索迭代次数结束之后，各个子群之间进行思想交流，实现子群间的混合运算。局部搜索和混合过程一直持续到定义的收敛条件结束为止，全局信息交换和局部深度搜索的平衡策略使得算法能够跳出局部极值点，向着全局最优的方向进行［7］。

对于S维优化问题，SFLA算法首先从已知可行域中随机生成P只青蛙组成初始群体，第i只青蛙表示问题的解为Xi=(xi1，xi2，…，xis)，计算每只青蛙的目标函数值f(Xi)，将每只青蛙根据其目标函数值按递减顺序排列，然后将整个青蛙群体划分为m个子群，每个子群中包含n只青蛙。

对于每一个子群，目标函数值最好的解记为Xb和目标函数值最差的解记为Xc，而群体中目标函数值最好的解记为Xg。在每次迭代中，只对子群中的Xc进行更新操作，其更新策略为

其中，j=1，2，…，s，Dmax≥Dj≥－Dmax，Dj为分量 j上移动的距离，Dmax为青蛙的最大移动步长。

经过更新后如果得到的解newXc优于原来的解oldXc，则取代原来族群中的解。否则，则用Xg取代Xb重复执行更新策略

如果仍然没有改进，则随机产生一个新的解取代原来的Xc。重复这种更新操作，直到设定的迭代次数，当所有子群的局部深度搜索完成后，将所有族群的青蛙重新混合、排序和划分族群，然后再进行局部深度搜索，如此反复直到达到事先设定的混合次数。

2.2 改进混合蛙跳算法

改进SFLA中，在文献［7］的基础上，提出了新的移动距离更新方式，每个族群进行局部深度搜索时，除了分量j上移动的距离引入上一次的移动距离，另外也加入了惯性权重系数，用来调节搜索能力。所以，式(2)变为

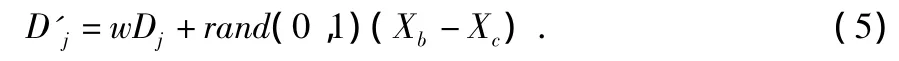
其中，w 为惯性权重系数，设置为0.9～0.4，D'j表示本次更新时分量j上移动的距离，Dj表示上次更新时分量j上移动的距离，群体初始化时，Dj以随机方式产生。

经过更新后如果得到的解newXc优于oldXc，则取代原来族群中的解，否则，按下式计算移动距离

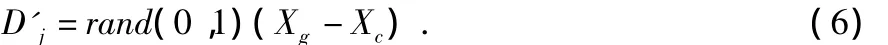
式(6)不包含上次移动距离，因为上次按式(5)更新后的解比原来的解更差，说明上次的移动距离不够理想，所以式(6)消除了历史不良影响，使得青蛙快速移动到全局最优解附近，从而可以加快收敛速度。如果newXc仍然没有改进，则随机产生一个新的解取代oldXc。改进SFLA中除了移动距离的计算方式与传统SFLA不同外，其他操作都与传统SFLA相同。

3 基于改进混合蛙跳的聚类算法

3.1 适应度函数设计

混合蛙跳算法在处理过程中以适应度函数为依据，利用种群中每个个体的适应度值来进行搜索。因此，影响混合蛙跳算法的收敛速度重要的是适应度函数的选取。对于每个个体，进行聚类的划分和重新计算各聚类的中心采用与K—均值算法相同的方式，然后根据每个聚类中的点与相应聚类中心的距离和作为判断聚类划分质量的评价函数，E越小表示聚类划分质量越好。

混合蛙跳算法的目的是搜索使评价函数最小的聚类中心，因此借助评价函数构造适应度函数如下

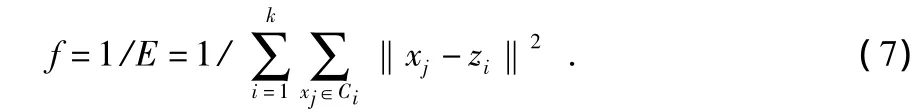
3.2 算法流程

本文提出的基于改进混合蛙跳的聚类算法流程如下:1)设定算法初始参数。

2)初始化种群和K个初始聚类中心。

3)对种群中的青蛙个体执行K-means操作。即，计算待分类集合{x1，x2，…，xn}到青蛙对应的K个中心的距离，根据距离将{x1，x2，…，xn}分类。

4)由分类计算出每只青蛙的适应度，按适应度大小对青蛙种群进行降序排列，随机生成Dj。

5)将青蛙群体分成m个族群，每个族群包含n只青蛙，确定各个族群中的最优解Xb、最差解Xc以及全局最优解Xg。

6)按式(3)和式(5)更新最差解 Xc得到 newXc，对newXc进行约束处理，若newXc优于oldXc，则取代oldXc;否则，按式(3)和式(6)更新最差解Xc得到新的newXc，再对newXc进行约束处理。更新族群中的最优解和最差解，局部迭代次数加1，重复执行以上过程，直到达到设定的最大局部迭代次数，跳至步骤(7)。

7)将族群合并成一个青蛙群体重新按适应度函数值对青蛙群体进行降序排列，全局迭代次数加1，跳至步骤(5)。重复执行以上过程，直到达到设定的全局最大迭代次数，算法终止，输出结果。

4 实验结果

通过UCI数据库中两组实际数据集Crude oil和Iris数据集来验证本文算法的性能。数据集信息概况如表1所示。

表1 Crude oil和Iris数据集的信息Tab 1 Information of Crude oil and Iris data set

为了能进一步验证本文算法的性能测试，将本文算法与基于传统混合蛙跳算法(SFLA)、基于遗传算法(GA)和基于蚁群算法(ACO)［8～10］的聚类结果进行了比较，通过运行多次来比较算法的性能，如表2，表3。

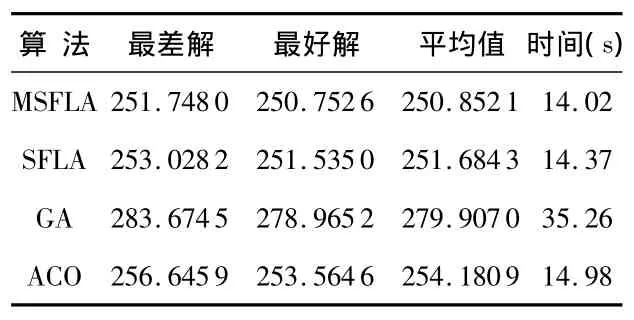
表2 四种算法对Crude oil聚类性能比较Tab 2 Comparison of Crude oil clustering characteristic by the four algorithms

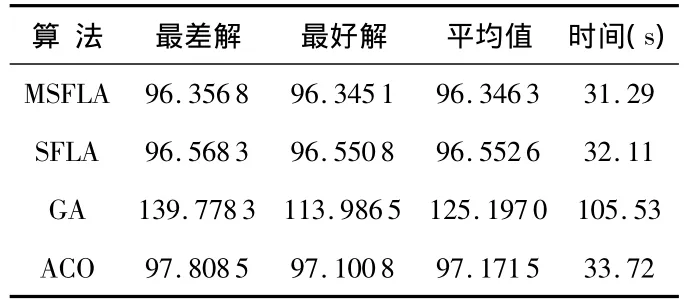
表3 四种算法对Iris聚类性能比较Tab 3 Comparison of Iris data clustering characteristic by the four algorithms

由以上表2、表3可以看出:基于改进混合蛙跳的聚类算法得到的结果，在收敛精度和速度上都能达到较好的聚类效果，优于基于传统混合蛙跳算法、遗传算法和蚁群算法的聚类方法。

5 结束语

K—均值聚类算法因其思想简单而成为聚类分析最常用方法之一，但K—均值法分类的结果依赖于选择的初始聚类中心，对于有些初始解K—均值法可能收敛于次优解。许多学者提出了基于智能优化算法的聚类方法来解决K—均值算法的这一缺陷。本文提出的基于改进混合蛙跳算法的聚类方法，引入了K—均值操作，提高了算法的局部搜索能力和收敛速度。实验结果验证了基于改进混合蛙跳算法的聚类方法的有效性和优越性。

［1］Jain A K，Murty M N，Flynn P J.Data clustering:A review［J］.ACM Computing Surveys，1999，31(3):264－323.

［2］杨小兵.聚类分析中若干关键技术的研究［D］.杭州:浙江大学，2005.

［3］Huang Z.Extensions to the K-means algorithm for clustering large data sets with categorical values［J］.Data Ming and Knowledge Discovery，1998(2):283－297.

［4］刘向东，沙秋夫，刘勇奎，等.基于粒子群优化算法的聚类分析［J］.计算机工程，2006，32(6):201－203.

［5］陆林花，王 波.一种改进的遗传聚类算法［J］.计算机工程与应用，2007，43(21):170－172.

［6］刘 白，周永权.一种基于人工鱼群的混合聚类算法［J］.计算机工程与应用，2008，44(18):136－138.

［7］郑仕链，楼才义，杨小牛.基于改进混合蛙跳算法的认知无线电协作频谱感知［J］.物理学报，2010，59(5):3612－3617.

［8］Amiri B，Fathian M，Maroosi A.Application of shuffled frogleaping algorithm on clustering［J］.International Journal of Advanced Manufacturing Technology，2009，45:199－209.

［9］Krishna K，Murty N.Genetic K-means algorithm［J］.IEEE Trans on SMC，1999，29:433－439.

［10］Shelokar P S，Jayaraman V K，Kulkarni B D.An ant colony approach for clustering［J］.Anal Chim Acta，2004，509:187－195.