基于改进PSO的可靠性稳健优化计算方法

叶南海 戚一男 陈 凯 翟银秀

湖南大学汽车车身先进设计制造国家重点实验室，长沙，410082

0 引言

传统可靠性计算一般基于概率密度分布理论、零部件材料强度与工作应力的均值和标准差来实现。近年来，国内外学者基于各种智能算法，对系统的可靠性与失效进行了计算、分析和预测［1－7］；文献［8－9］在稳健设计信息基础上，根据粒子群算法将迭代适应值模糊化处理，对某乘用车辆的前轴可靠性进行了计算；文献［10－13］运用反问题等分析方法，对可靠性进行了优化计算求解。

上述研究方法均存在一定程度的局限性，本文针对这些局限性，根据现代设计方法与稳健设计原理，以可靠性的一阶导数和体积最小作为目标函数，建立了可靠性优化计算的多目标约束优化数学求解模型，提出了动态加速常数和速度自适应的改进粒子群算法，并通过编写的计算机程序代码，实现了多目标约束优化的数值化求解。

1 可靠性设计的随机摄动法

可靠性设计的一个目标是可靠度：

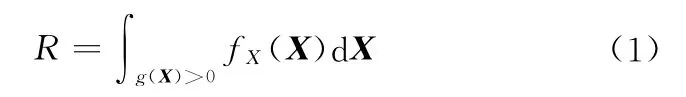
式中，fX（X）为基本随机参数的联合概率分布密度，X＝（x1，x2，…，xn）T；g（X）为状态函数，g（X）＞0表示安全状态；g（X）≤0表示失效状态。

把随机参数向量X和状态函数g（X）表示为

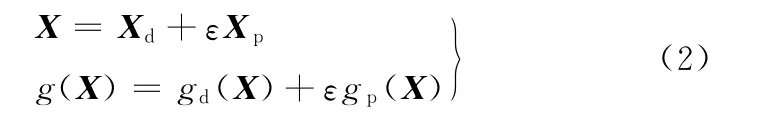
式中，ε为参数。

对式（2）取均值、方差，有

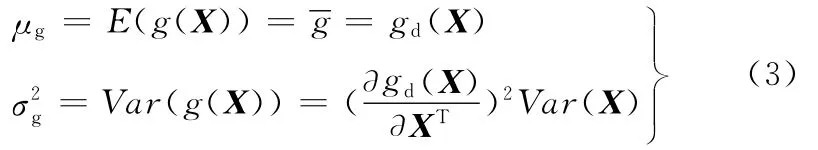
式中，Var（X）为基本随机参数的方差向量。

把状态函数g（X）对基本随机变量X求偏导数，有

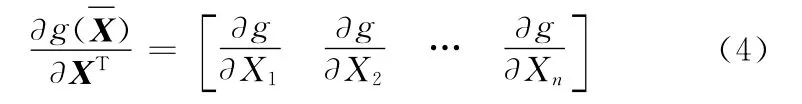
把式（4）代入式（3），可以得到状态函数方差的表达式，其可靠性指标定义为

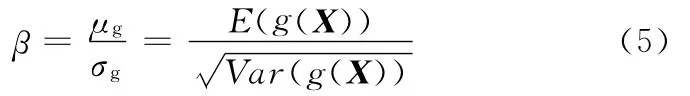
在基本随机参数向量X服从正态分布时，可以获得可靠度的一阶估计量：

式中，Φ（·）为标准正态分布函数。

2 多目标可靠性稳健优化设计模型

由于可靠性稳健优化设计是要求可靠度对设计数据、工作载荷和材料等参数的变化不敏感，所以将可靠性稳健优化设计问题转化为多目标优化设计来处理，即

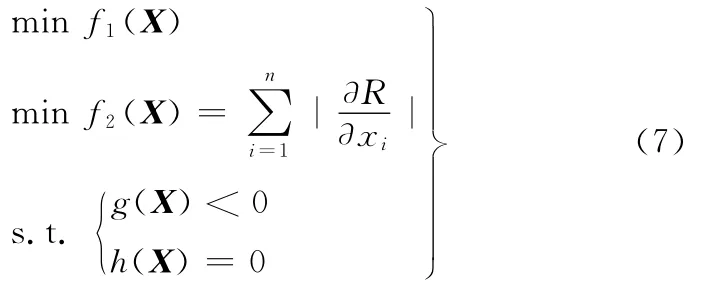
式（7）中，目标函数f1（X）可以为质量、体积等问题；目标函数f2（X）为可靠性的一阶导数计算；可靠度的一阶估计量R，表示对构成可靠度计算的各个变量参数执行一阶导数求解，之后进行求和运算。目的在于把自变量的变化对可靠度的影响降到最低，使可靠度具有不灵敏性，从而实现可靠性的稳健鲁棒设计。

在多目标优化中，通常不存在能使得所有目标函数同时优化的最优解。也就是说，如果可行解X是某些目标函数的最优解，但X常常不会是其余目标函数的最优解。因此，绝对最优解在多目标优化问题中通常是不存在的，考虑到各目标函数的权重，采用量纲一化处理。式（7）即可表示为

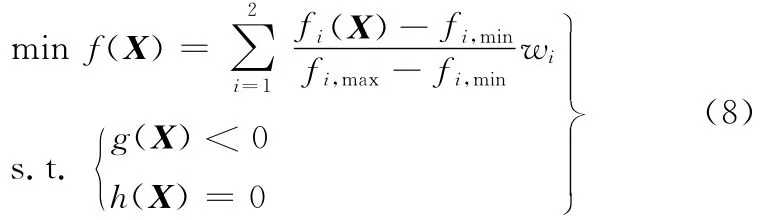
式中，fi，min、fi，max和wi分别为各目标函数的最小值、非理想最大值和权重系数。

式（8）采用基于参数策略（加速常数和速度）的改进粒子群算法实现数值化求解。

3 基于参数策略的粒子群算法求解

PSO初始化为一组随机解（随机粒子），通过迭代利用粒子在解空间追随最优的粒子进行搜索。PSO在每次迭代中，粒子通过跟踪2个极值来更新自己。一个是粒子本身找到的最优解，称其为个体极值pbest；另一个则是整个种群目前找到的最优解，称其为全局极值gbest。在找到这2个极值后，粒子根据下式进行自己的速度和位置更新：

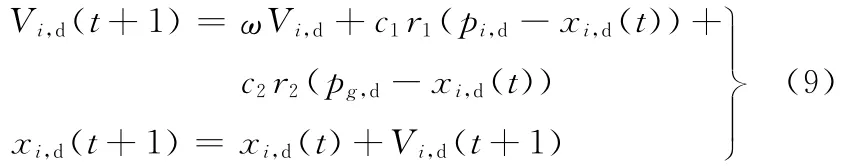
式中，c1、c2为加速常数（学习 因 子）；ω 为 惯性 权 重；r1、r2为介于（0，1）之间的随机函数；pi，d为局部最优解；pg，d为全局最优值。

式（9）中，Vi，d∈ ［Vmin，Vmax］，由三部分组成：第一部分是粒子的先前速度部分，这部分说明粒子目前的状态；第二部分是个体的认知部分，这部分使粒子有较强的全局搜索能力，避免陷入局部极小；第三部分是社会共享信息部分，这部分能使粒子从其他优秀粒子中吸取经验，加强搜索能力。

影响粒子群算法性能的参数主要有：惯性权重ω、加速常数c1、c2和最大限制速度Vmax，因此基于参数的改变问题也是提高寻找最优解精度和效率的有效途径之一。标准PSO是基于调整惯性权重的自适应算法，它与其他进化算法比较，尽管能够以非常快的速率找到局部好解，但是在寻找全局最优解的能力方面还是相对弱一些。在标准PSO算法中，通常采用ω随进化代数的增加而线性递减的方式，在这种取值方法中，存在一些问题。首先，如果在运行初期探测到较优点，则希望能够迅速收敛于最优点，而ω的线性递减减缓了算法的收敛速度；其次，在算法的运行后期，随着ω的减小，全局搜索能力下降，多样性减弱，容易陷入局部最优。为此，本文提出两种基于参数策略的改进算法，并基于加速常数c1、c2和Vmax及惯性权重ω，协同探讨控制算法朝最优解方向进化的途径，以提高PSO算法的性能。

3.1 C－PSO算法

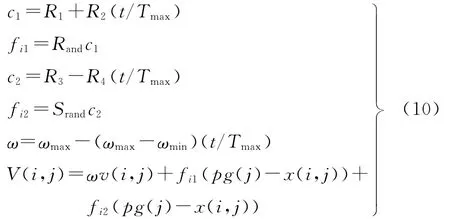
式中，R1、R2、R3、R4为初始设定的定值；Rand为0～1的任意随机数；ωmax、ωmin为权重的最大值、最小值；t、Tmax分别为当前进化代数和最大进化代数。

通过设定初始常数R1、R2、R3、R4来实现对c1、c2的调节，C－PSO算法的特点是，在优化的早期，鼓励粒子在整个搜索空间移动，而在优化的后期，提高趋于最优解的收敛率。

3.2 V－PSO算法

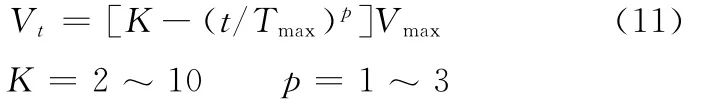
当Vi，d＞Vt，则Vi，d＝Vt；当Vi，d＜－Vt，则Vi，d＝－Vt。其中，K、p为控制尺度系数大小的正常数。V－PSO算法引入了自适应尺度系数K－（t／Tmax）p，目的在于使其随着进化的代数增加而下降，从而控制搜索的规模，提高收敛的效率。

基于参数策略的多目标约束优化求解PSO算法流程，如图1所示。

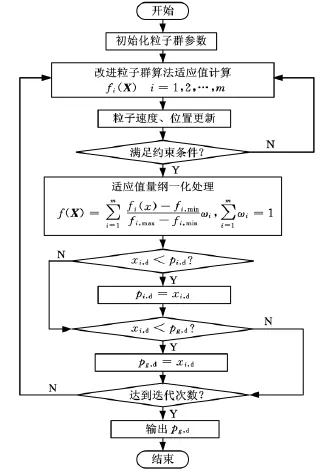
图1 改进PSO算法流程图

4 算例

某矿用提升绞车软启动调速系统采用行星齿轮传动，中心轮输入扭矩为2521.2kN·m，其齿数与行星轮齿数相同，材料为40Cr渗氮处理，硬度为245～288HB，内齿圈采用45钢调质，硬度为229～286HB。要求在保证其轻量化的前提下，完成其可靠性稳健设计。

4.1 数学模型

（1）设计变量。取中心轮齿数za、模数m和齿宽系数φd作为设计变量，行星轮齿数zc、内齿圈齿数zb，则按照zc＝za，zb＝za＋2zc得到。

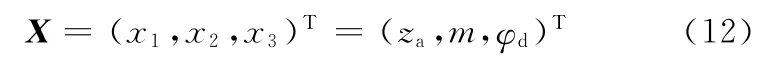
（2）目标函数。要求整个行星轮系的体积最小，质量轻量化，其意可表示为

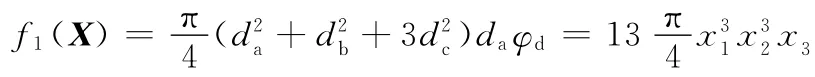
要实现行星轮系的稳定可靠度和稳健设计，则必须保证可靠度不受系统参数变化的影响，或其影响最小，即鲁棒性。这里假设行星轮系中心轮齿面许用接触应力δ及偏差σδ保持不变，行星轮系传动比恒定。根据文献［14］，中心轮齿面的工作接触应力S与可靠度联结系数β可表示为

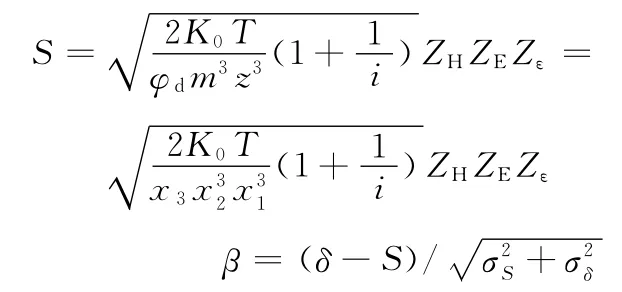
式中，K0、T、ZH、ZE、Zε均为相关的已知常数。

根据式（5）可靠性指标定义，本文算例的可靠性稳健设计可表示为

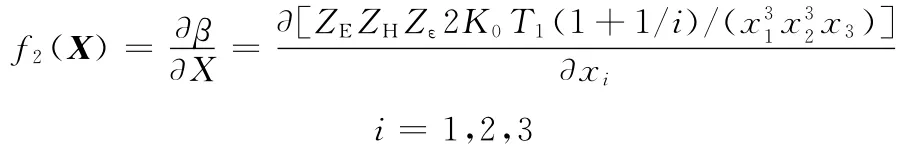
故目标函数为

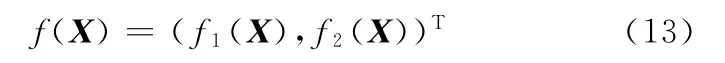
（3）约束条件。齿面接触应力小于许用接触应力：

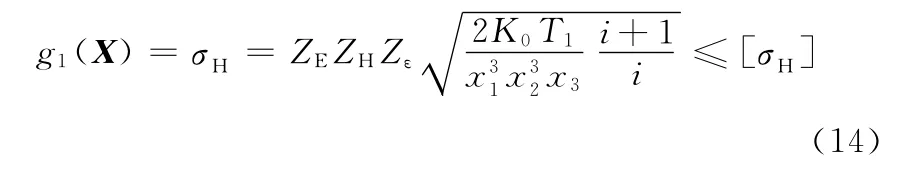
中心轮的齿根弯曲应力应小于其许用弯曲应力：

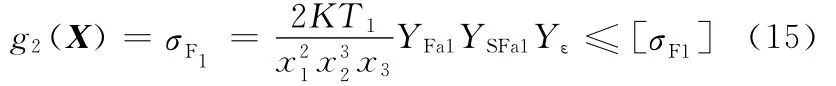
4.2 动态加速常数粒子群算法求解（C－PSO）

设17≤x（1）≤40，8≤x（2）≤15，0.5≤x（3）≤2；选取 md＝10，Mdim＝3，vmin＝－1，vmax＝1，ωmin＝0.3，ωmax＝1.8，Tmax＝1000，f1，min（x）＝4×107，f2，min（x）＝180，根据前述双目标函数与约束条件编写MATLAB计算机程序，初始设定常数R1、R2、R3、R4的取值与迭代算法收敛、优化结果如表1所示（表中，Yfitness为函数适应值）。

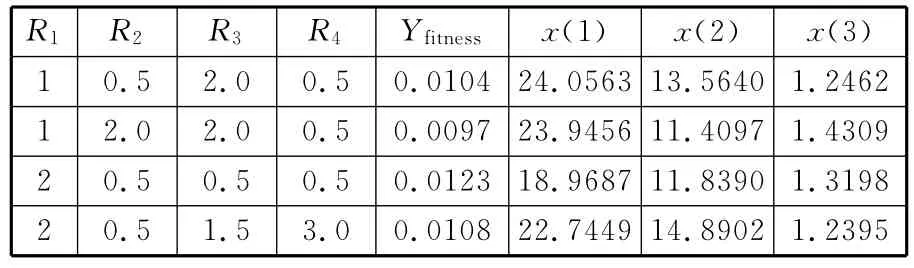
表1 C－PSO参数设置与求解结果

基于不同R1、R2、R3、R4取值的C－PSO算法的函数适应值迭代曲线如图2所示。

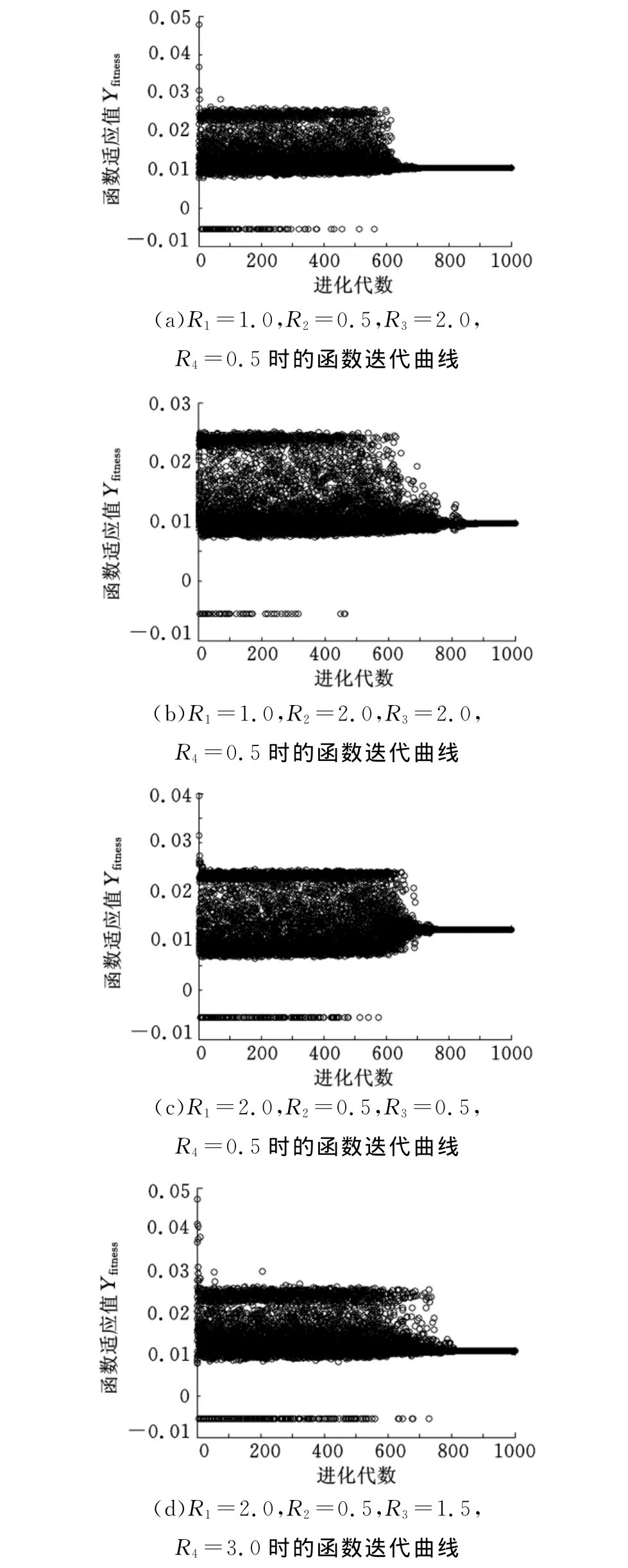
图2 不同R1、R2、R3、R4参数的C－PSO迭代曲线关系图

各个分目标函数在考虑权重系数之后，经过量纲一化处理得到的综合目标函数的适应值为Yfitness，从表1中可以看出，其最小值为0.0097；目标函数在经过大约700次迭代后，出现收敛；调整初始设定常数R1、R2、R3、R4的值，函数收敛速度将会发生变化，参数越小，收敛速度越快。

4.3 速度自适应粒子群算法求解（V－PSO）

设17≤x（1）≤40，8≤x（2）≤15，0.5≤x（3）≤2；选取c1＝2，c2＝2，m＝20，Mdim＝3，ωmin＝0.4，ωmax＝1.3，f1，min（x）＝4×107，f2，min（x）＝180，Tmax＝200，K、p、Vmax取值与迭代算法收敛、优化结果如表2所示。

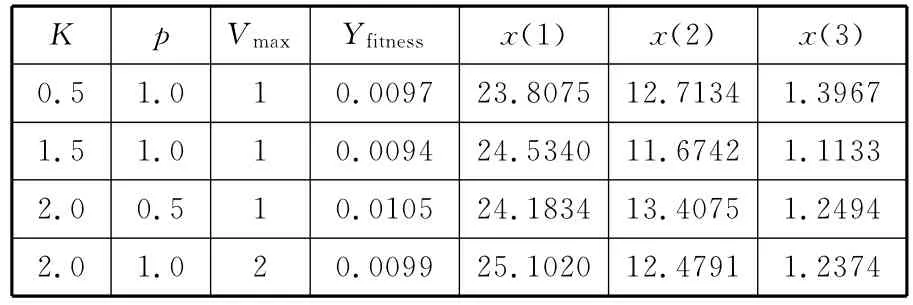
表2 V－PSO参数设置与求解结果

基于不同K、p、Vmax取值的V－PSO算法的函数适应值迭代曲线如图3～图6所示。

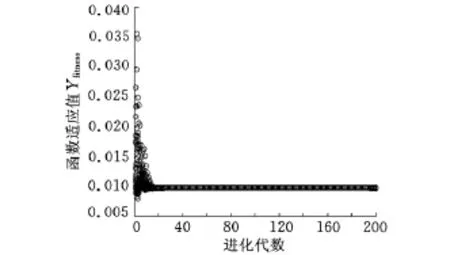
图3 K＝0.5，p＝1，Vmax＝1时的函数迭代曲线

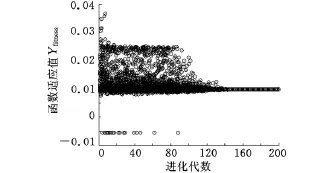
图4 K＝1.5，p＝1，Vmax＝1时的函数迭代曲线

从表2和图3可以看出，目标函数最小值为0.0094，当K、p、Vmax的取值改变时，迭代收敛情况将发生明显变化，一般来说，取值越小，则收敛越快。

综上所述，本算例的优化结果（圆整）为：模数12mm、齿宽300mm、中心轮与行星轮齿数均为25、材料选用40Cr渗氮；内齿圈齿数为77。

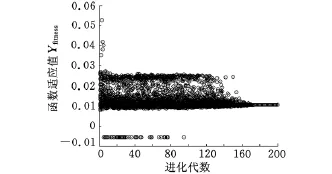
图5 K＝2，p＝0.5，Vmax＝1时的函数迭代曲线

图6 K＝2，p＝1，Vmax＝2时的函数迭代曲线

5 结束语

针对目前已有的关于可靠性优化设计算法的单一性，提出了一种全新的可靠性稳健优化设计的计算方法。将可靠性的灵敏度作为优化目标，体现了可靠性的稳健设计；通过基于参数策略（动态加速常数和速度自适应）的改进PSO算法在数学模型求解程序代码中的应用，实现了可靠性稳健优化计算的数值化求解，同时也为多目标约束优化问题的求解提供了一种计算方法。算例表明，基于改进PSO的可靠性稳健优化计算方法，具有结果信息简单实用，适宜工程应用的优点。

［1］Sankaran M，Ramesh R.Validation of Reliability Computational Models Using Bayes Networks［J］.Reliability Engineering and System Safety，2005，87：223－232.

［2］Ozge D，Jose E，Ramirez M.A Generic Method for Estimating System Reliability Using Bayesian Networks［J］.Reliability Engineering and System Safety，2009，94：542－550.

［3］郏宣耀，李欢，滕少华，等.自适应变邻域混沌搜索微粒群算法［J］.计算机工程与应用，2007，43（31）：90－92.

［4］Jin C，Cheng X.A New Artificial Neural Network－based Response Surface Method for Structural Reliability Analysis［J］.Probabilistic Engineering Mechanics，2008，23：51－63.

［5］Hosni E，Mesbahi Y.Reliability Analysis of Structures Using Neural Network Method［J］.Probabilistic Engineering Mechanics，2006，21：44－53.

［6］Lin Minsheng.Linear－time Algorithms for Computing the Reliability of Bipartite and（＃62）Star Distributed Computing Systems［J］.Computers ＆Operations Research，2003，30：1697－1712.

［7］Dixiong Y.Chaos Control for Numerical Instability of First Order Reliability Method［J］.Commun Nonlinear Sci.Numer.Simulat.，2010，15：3131－3141.

［8］魏秀业，潘宏侠.粒子群优化及故障诊断［M］.北京：国防工业出版社，2010.

［9］张义民，刘仁云，于繁华，等.车辆前轴的多目标可靠性稳健优化设计［J］.机械设计与研究，2006，22（4）：82－84.

［10］Mohsine A，Hami E.A Robust Study of Reliability－based Optimization Methods Under Eigenfrequency［J］.Comput.Methods Appl.Mech.Engrg.，2010，199：1006－1018.

［11］Chang Y C，Chang S L.Innovative Reliability Allocation Using the Maximal Entropy Ordered Weighted Averaging Method［J］.Computers ＆Industrial Engineering，2009，57：1274－1281.

［12］Ikjin L，Choi K K.Inverse Analysis Method Using MPP－based Dimension Reduction for Reliability－based Design Optimization of Nonlinear and Multi－dimensional Systems［J］.Comput.Methods Appl.Mech.Engrg.，2008，198：14－27.

［13］Mahdavi S J，Mohammadi K.Improved Singlepass Approach for Reliability Analysis of Digital Combinational Circuits［J］.Microelectronics Reliability，2011，51：477－484.

［14］刘惟信.机械可靠性设计［M］.北京：清华大学出版社，2006.