橡胶轮胎支撑圆筒混合机受力分析

万书华，白明华，任素波

(燕山大学 机械工程学院，河北 秦皇岛 066004)

0 前言

圆筒混合机是烧结厂和球团厂主要冶金设备之一，配置在配料设备和烧结设备之间［1］。混合机内混合料的混合效果，直接影响烧结矿的质量，进而影响高炉的生产率。橡胶轮胎支撑的混合机由于具有优越的力学性能［2］，在烧结厂和球团厂应用广泛。由于采用多个橡胶轮胎支撑，其受力大小的计算属于多次静不定问题。以往对于橡胶轮胎受力的求解方法大致有两种:

(1)认为各个支点处轮胎的受力情况一样，这样大大简化计算，只需要把总的受力除以橡胶轮胎个数，便可以得到各个轮胎的受力情况，这种方法对于估算轮胎受力比较实用。但实际上每个轮胎的受力因为轮胎之间的间距不同而不同。

(2)采用三弯矩方程求解，把混合机简化为连续梁的形式，这样所得结果比较接近实际情况。但是对于有n个轮胎支撑的混合机，需要列写n－2个弯矩方程，随着轮胎的增多，方程也就越多，求解比较麻烦。

本文试图采用新的方法——弯矩分配法计算各个轮胎的受力，采用弯矩分配法不需要求解多元一次方程组，便可以迅速求出足够精确的解。本方法的特点是步骤明了，易于计算，而且不需要借助于计算机求解，便迅速可得出结果。

1 弯矩分配法基本原理

根据叠加原理，将受力件的受载状态分解为两个简单的状态，即固定状态和自由状态，这些简单状态的受力特点根据材料力学相应公式可以直接得出结果。将计算结果相叠加，即可求得原始受载状态下的受力分布［3］，如图1所示。

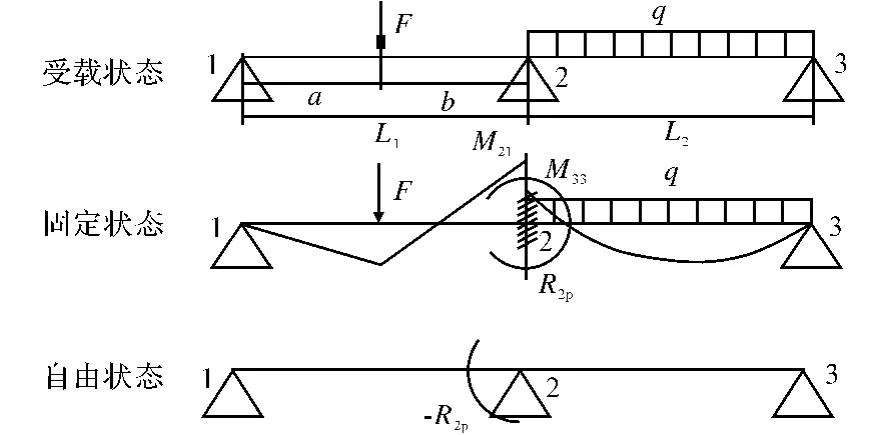
图1 弯矩分配法原理示意图Fig.1 Principle diagram of bending moment distribution method

固定状态:假定中间支撑点2固定，使其成为固定端，固定端在原载荷作用下产生的各固定端弯矩根据材料力学可以分别求得:

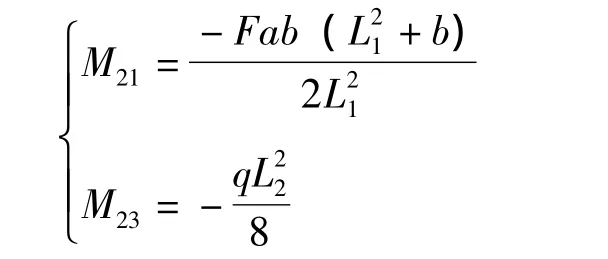
式中，M21为杆件12的2端加于该杆的杆端弯矩，以顺时针为正为N·m;M23为杆件23的2端加于该杆的杆端弯矩，以顺时针为正，N·m。

节点2被固定，限制了角位移。使节点2固定的本质是添加了一个额外的弯矩R2p，称之为不平衡弯矩，R2p=ΣM2=M21+M23。

自由状态:为了消除固定状态而施加的弯矩R2p，恢复原有受载状态，需要在节点2处施加弯矩－R2p，自由状态各杆弯矩可用分配系数和传递系数计算。

1.1 杆端传递系数CAB

在杆件AB中，使杆端A产生单位转角需要在A端添加弯矩 MAB，同时在 B端产生弯矩MBA，称之为传递弯矩，其比值CAB=MBA/MAB称为传递系数，传递方向为A→B。两端固定，其传递系数为

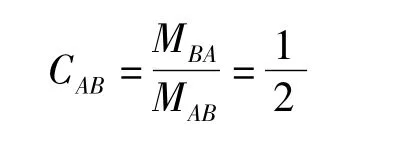
A端固定，B端铰接，其传递系数为

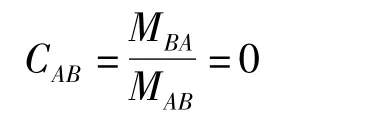
1.2 杆端弯矩分配系数

不同杆件的端点相交于同一刚性节点，在该刚节点上施加外弯矩M时，相交的各杆将以某种比例共同承担弯矩M，每个杆端承担的比例为Mn/M成为该杆端弯矩的分配系数μn。连续梁分配系数求解，如图2所示。

图2 连续梁示意图Fig.2 Diagram of continuous beam

在A节点作用力矩M，则有

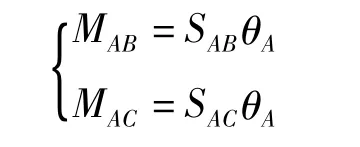
式中，SAB为刚度系数，在数值上等于使杆端产生单位转角时需要在转动端施加力矩;MAB为杆AB段因弯矩M而承受的弯矩;MAC为杆AC段因弯矩M而承受的弯矩。

在A节点处，有ΣM=0，则有

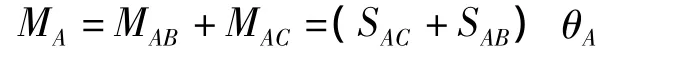
得

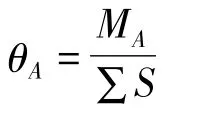
将θA带入式 (1)可得

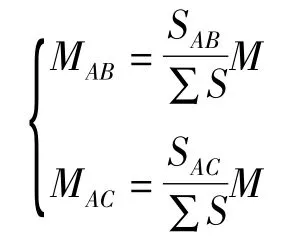
由分配系数定义可以得

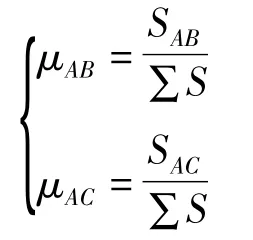
连续梁求解截面弯矩方法归纳如下

节点A作用力偶载荷M，按各杆的分配系数分配给各杆的近端;远端弯矩等于近端弯矩乘以传递系数，求解时杆端弯矩规定以顺时针为正方向。

2 橡胶轮胎受力求解

为了简化计算，做如下假设:

(1)混合机的长径比大，计算轴向力时，将其简化为梁计算;

(2)认为筒体的各部分截面惯性矩相等;

(3)作用在筒体上的载荷为均布载荷;

(4)筒体的长度远大于橡胶轮胎宽度，根据圣维南原理，计算筒体受力时将轮胎对简体的作用力简化为集中力。

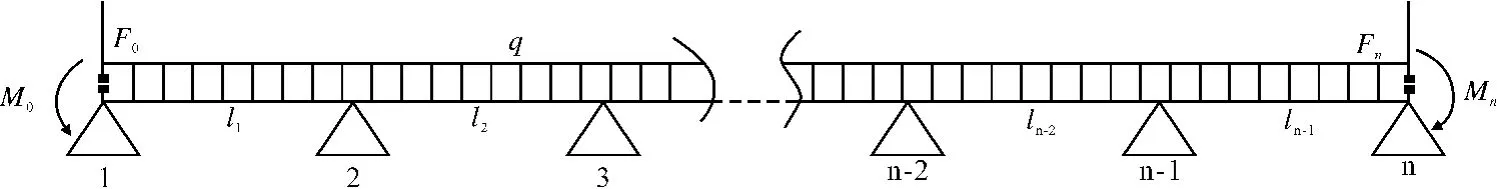
图3 圆筒混合机支点及载荷示意图Fig.3 Diagram of fulcrum and load on drum mixer

2.1 支点截面弯矩求解

混合机单侧由n个轮胎支撑，支点分别为△i，li为支点之间的间距，第一段距离为l1，最后一段距离为ln－1，q为均布载荷;Mi、Fi分别为两端悬伸段载荷简化到相应支点的力矩和力。求解步骤:

(1)将中间支撑点2～n－1固定，求出在原载荷作用下各个支点处的弯矩，以顺时针方向为正，当i=2～n－2时，

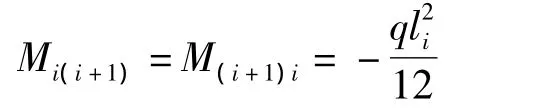
当i=2、n－1时，弯矩分别为

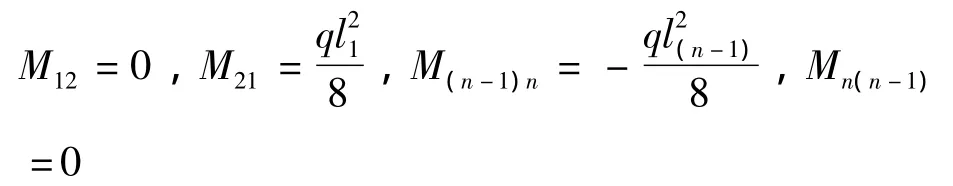
(2)放松中间节点2～n－1，利用传递系数和分配系数求解各杆端弯矩。

分配系数为

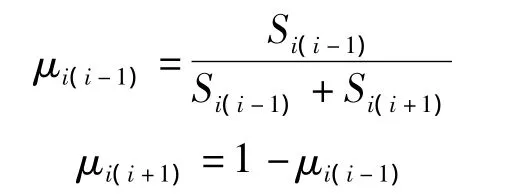
传递系数为

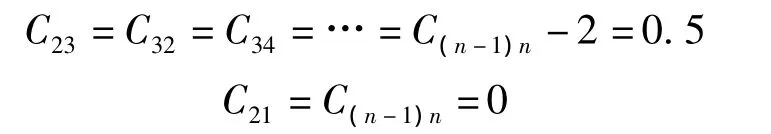
杆端弯矩为

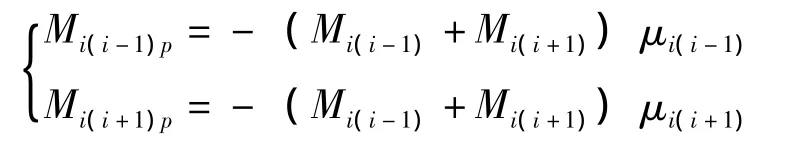
(3)将上述两结果叠加即可求出各支点处弯矩即受载状态的支座截面弯矩为

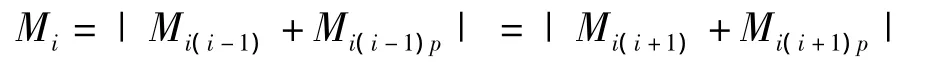
2.2 每个支座受力计算

求出各个支座的截面弯矩后，各支座的径向力由两部分组成。即

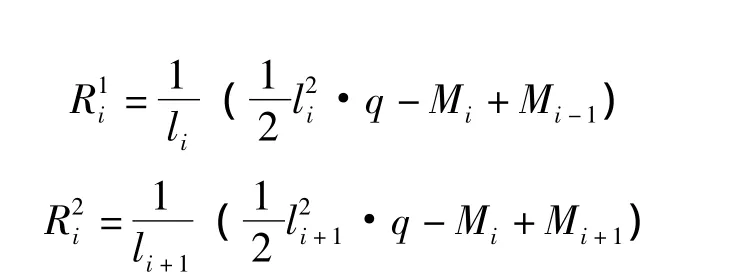
各支座的总径向力为

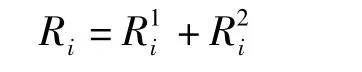
3 计算实例

以某厂3 m×12 m橡胶轮胎摩擦传动圆筒混合机为例，采用弯矩分配法计算各个支座的受力。其原始参数见表1［3］，计算结果见表2。

表1 原始参数表Tab.1 Origional parameters

表2 部分计算结果Tab.2 Partial calculated results

从表2中可以看出，主动侧受力远远大于从动侧受力。主要是因为混合机在工作时，物料随着筒体旋转，然后泻落，物料大部分重量几乎压在一侧，而且由于旋转产生离心力，导致混合机的两侧受力相差很多。合理布置两侧的支点位置。有利于减小差距，提高轮胎使用寿命。得出部分计算结果后，采用弯矩分配法计算轴向方向上各个轮胎受力。各个轮胎受力计算结果如图4～图6所示。

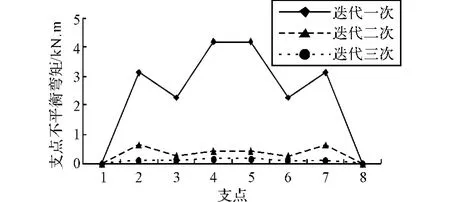
图4 各支点不平衡弯矩变化图Fig.4 Variation of unbalanceed bending moment at each fulcrum

图5 从动侧支点受力图Fig.5 Stress on slave side-fulcrum

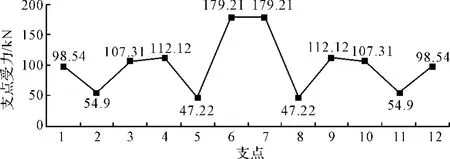
图6 主动侧支点受力图Fig.6 Stress on active side-fulcrum

从动侧各个支点力总和为36.67+38.47+33.98+53.475+53.475+33.98+38.47+36.67=325.19 kN，与总的从动侧径向力324.47 kN基本一致，主动侧各个受力总和为1198.6kN，与主动侧总受力大小1198.66 kN基本一致。

如图4所示，第1个支点处和第8个支点处没有不平衡弯矩，其原因在于求解过程中，只固定中间支点的6个支点，所以第1个支点和第8个支点处不会产生不平衡弯矩。经过三次迭代计算，支点处的不平衡弯矩很小，可以忽略不计。由于采用的是对称布置，支点的不平衡弯矩呈现对称分布。从图5、图6中可以看出，轮胎对称布置，因此支点的受力也呈现对称分布。此外，从动侧第4个支点与第5个支点处的支撑力比其它支点处的受力大约1.5倍，原因在于第4个支点与第5个支点的间距L4比其它支撑点之间的距离大，因此对应的受力也大。主动侧第6个支点和第7个支点处的受力明显大于其它支点处受力，因为这个支点处的间距比较大。对比图5和图6，主动侧各个支点受力明显大于从动侧各个支点受力。因此在满足操作空间的前提下，合理布置轮胎径向和轴向的支撑位置，使轮胎的受力均匀，有助于提高轮胎使用寿命，提高生产效率。

4 结论

在分析以往文献及相关理论的基础上，提出了采用弯矩分配法计算轴向上各个轮胎的受力，其步骤清晰，收敛速度快。从计算过程可以看出，不平衡弯矩－Rp衰减很快，只需要三次分配，就可以得到足够精确的结果，而且求解过程非常清楚明了。通过计算实例进一步说明采用弯矩分配法计算轮胎受力的特点。

［1］杨占凯，张春晓.圆筒混合机齿轮副强度的计算［J］.有色矿冶，2008，24(4):45－46.

［2］张超.当代混合机的结构原理及发展趋势 ［J］.矿山机械，2010，38(16):12－15.

［3］王来，王彦明.结构力学 ［M］.北京:机械工业出版社，2010.

［4］宋执武，白明华.圆筒混合机支座设计计算 ［J］.重型机械，2000(6):37－40.