形态小波在轧机扭矩信号中的应用

孙志辉，吕文泉，马建壮

(北京科技大学机械工程学院，北京 100083)

0 前言

随着现代化工业化进程的加快，众多行业对冶金材料的表面质量、尺寸精度等要求越来越高，板带轧机生产过程的振动问题成为了一个亟待解决的重要课题［1］。在实际生产过程中所测到的轧机振动信号往往具有非线性非平稳的，所以，非线性非平稳处理方法应用于轧机振动信号已经成为轧机故障诊断发展的方向。

形态小波作为一种非线性分析方法，在此框架的基础上选择不同的形态学算子可以产生一系列具有特定处理效果的形态小波变换，所以形态小波兼有形态学理论、小波理论和多分辨率分析技术所具备的优势和算法特点［2］。而且分析过程中是采用的加减或求极大极小运算，运算速度快，所以对实时性要求较高的场合有着很强的吸引力。

1 形态小波分析方法原理

由于轧机振动信号常常会表现出非线性特征，所以用非线性的形态小波降噪算法能更好地提取信号的非线性特征。基于形态小波降噪算法的故障特征提取方法，其主要流程如图1所示。

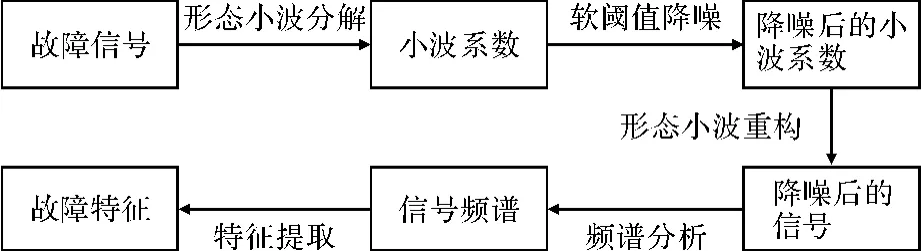
图1 基于形态小波降噪的特征提取方法的主要流程Fig.1 Main flow of feature extraction based on morphological wavelet

基于形态小波降噪的特征提取方法主要步骤如下:(1)信号的形态小波分解。选择一个或几个形态分析算子并确定分解的层次，然后进行分解计算。(2)形态小波分解高频系数的阈值量化。对各个分解尺度下的高频系数选择一个阈值进行软阈值量化处理消噪。(3)形态小波重构。利用形态合成算子把信号重构，重构后的信号即为降噪后的信号。(4)从形态小波降噪后的信号频域中提取特征信息。

1.1 形态Haar小波

本文将利用具有膨胀算子的形态Haar小波对信号进行分解，其分析算子和合成算子如下［3］:

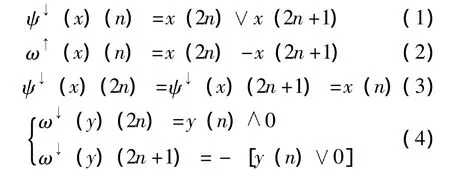
式中，ψ↑为信号分析算子，ω↑为细节分析算子，ψ↓为细节合成算子，为膨胀算子 (取大运算)，为取小运算。

1.2 软阈值降噪

为了达到提取信号中不同成分的目的，必须对分解后的系数进行降噪处理。在实际应用当中，默认阈值消噪和给定软阈值消噪这两种处理方法最为广泛。常用软阈值消噪的处理公式如下［4］:

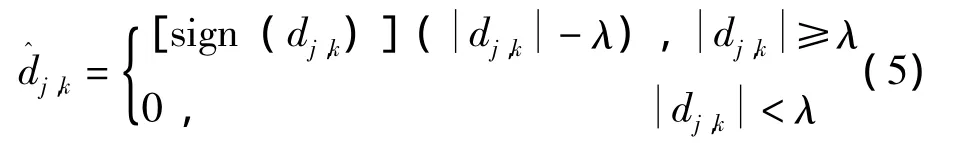
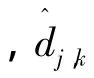
而在本例中消噪公式刚好相反，是将绝对值大于阈值的系数置零，即

这样处理有些类似低通滤波器效果，其主要目的是将高频成分滤掉，然后提取其它成分。

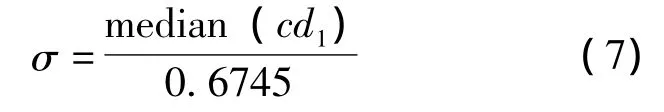
其中，cd1为第一层小波系数，median(cd1)表示中值算子。

2 轧机扭矩信号的分析

图2为某轧钢厂冷连轧F4轧机的扭矩和垂直加速度振动信号。采样频率为2000 Hz，图2a为F4轧机传动侧扭矩信号，图2b为F4轧机垂直振动加速度信号。

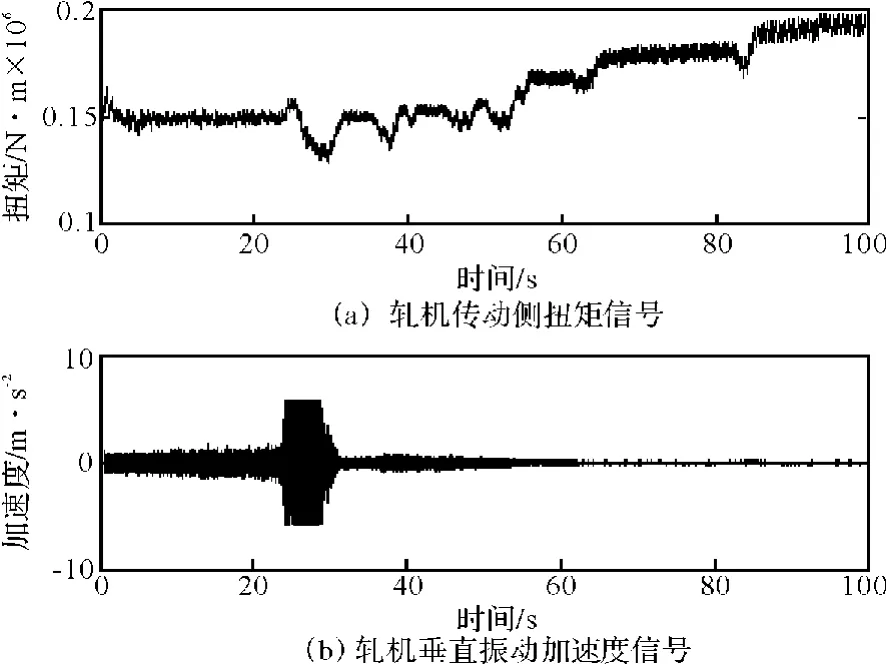
图2 轧机扭矩和垂直加速度信号Fig.2 Signals of rolling mill torque and vertical acceleration

在图2b中，F4轧机在23.29 s时发生了较强的垂直振颤。取信号的24～25 s做进一步分析，F4传动侧扭矩信号的时域和频域图见图3，图4为F4轧机垂直加速度的时域和频域图。

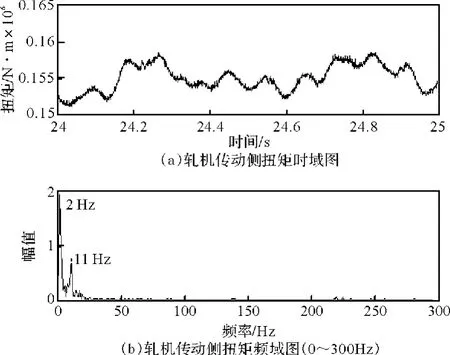
图3 传动侧扭矩信号的时域和频域图Fig.3 Time domain and frequency domain of torque signal on drive side

从图4b中可以看出，当F4轧机发生大幅度振动时，振动的主频率为225 Hz;在图3b中看到扭矩信号的优势频率是2 Hz、11 Hz的低频成分。如果轧机的垂直振动和扭转振动存在耦合，那么在轧机发生垂直振颤时扭矩信号中应当也有所体现。下面采用上节提到的形态小波降噪特征提取方法对轧机扭矩信号进行分析。

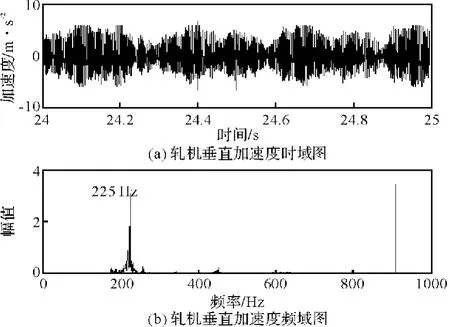
图4 轧机垂直加速度信号的时域和频域图Fig.4 Time domain and frequency domain of vertical acceleration signal

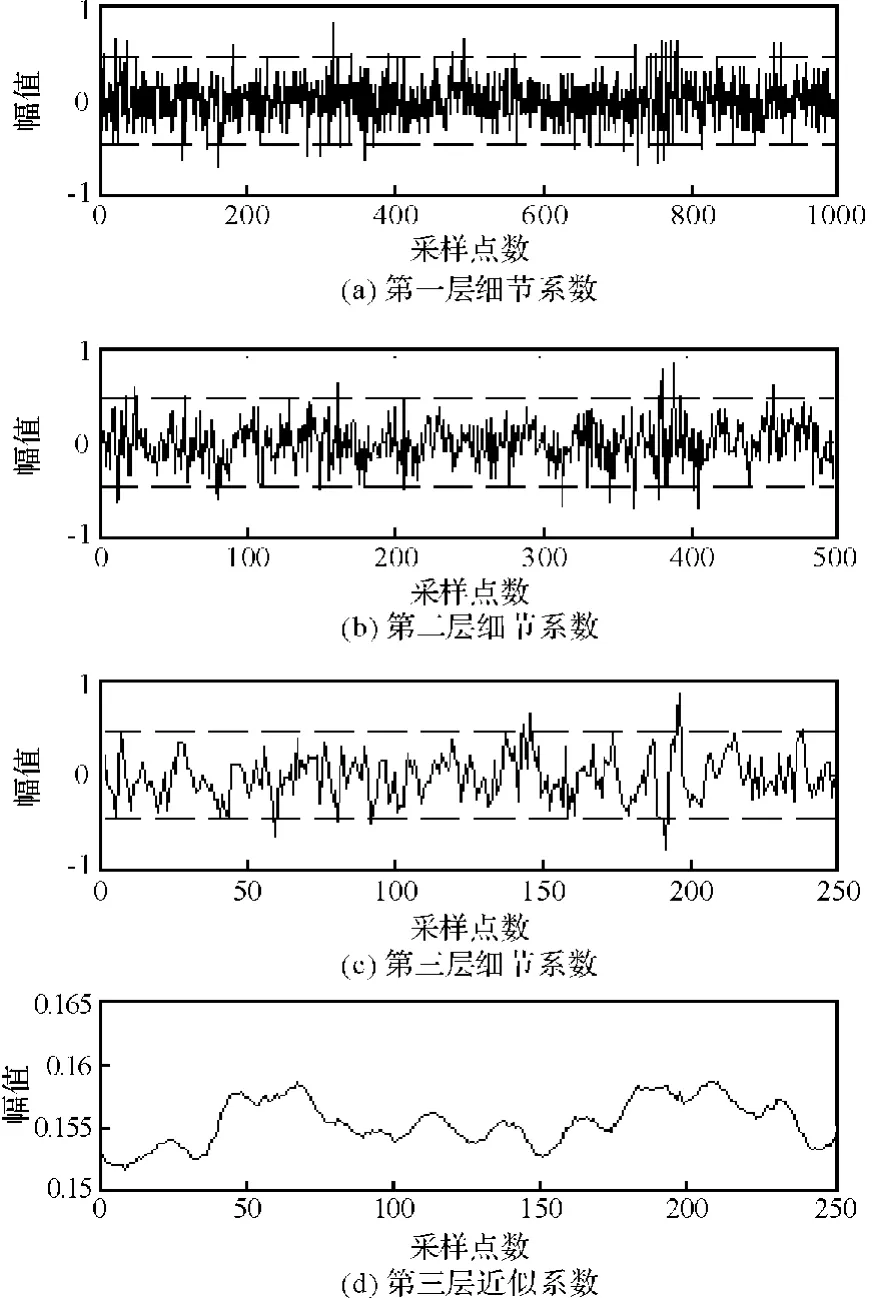
图5 形态Haar小波三层分析后的细节和近似系数Fig.5 Detailed and approximate coefficients after morphological Haar wavelet three-tier analysis

利用具有膨胀算子的形态Haar小波对F4轧机传动侧扭矩信号的24～25 s进行三层分解，分解后得到的细节和近似系数如图5。

对细节系数进行软阈值消噪。利用上节中提到的软阈值降噪方法对第一、二和三层细节系数进行处理，通过第一层小波系数 (细节系数)计算得到的小波降噪阈值为图5中虚线所示。另外，由于信号中大部分都是低频成分，而这些并不是我们所关心的，所以在信号重构过程中将低频成分置零，即将第三层近似系数全部置零。

具有膨胀算子形态Haar小波分解降噪重构的信号时域图和频域图见图6。在图6b中可以明显的看到225 Hz的振频。

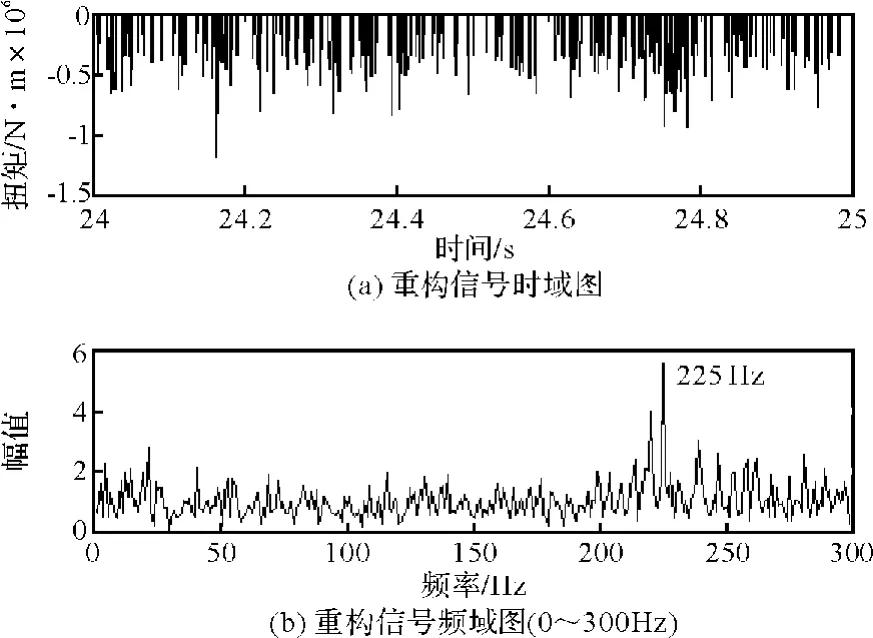
图6 形态Haar小波分析后时域图和频域图Fig.6 Time domain and frequency domain after morphological Haar wavelet analysis

3 结论

本文所应用的软阈值降噪方法有效抑制了高频成分和噪声，在信号形态小波重构的过程中去掉了低频成分，成功从轧机传动侧扭矩信号中提取出了轧机颤振的故障频率，证明了轧机系统的耦合性。

［1］杨旭，童朝南.板带轧机振动问题研究 ［J］.钢铁研究学报，2009，21(11):1-11.

［2］郭晓鑫.基于数学形态学的信号分析方法在设备故障诊断中的应用研究 ［D］.北京:北京科技大学，2009.

［3］章立军，黎敏，阳建宏，等.基于自适应形态小波的轧机电气信号压缩方法［J］.北京科技大学学报，2011，33(3):353-357.

［4］陈涛，徐小力，王少红.基于小波包惩罚函数的烟机振动信号软阈值降噪［J］.北京理工大学学报，2010，30(8):906-909，914.

［5］杨建国.小波分析及其工程应用 ［M］.北京:机械工业出版社，2005:68.

［6］Simon-Zorita D，Ortega-Garcia J，Cruz-Llanas S，et al.Minutiae extraction scheme for fingerprint recognition systems［J］.IEEE International Conference on Image Processing 2001，Thessaloniki，Greece，2001，21(3):254-257.