离散数学中的闭包概念及应用

吴明芬，瞿赟昀

（五邑大学 计算机学院 广东江门529020）

0 引言

离散数学以研究离散量的结构和相互关系为主要目标，其研究对象一般是有限或可数个元素组成的集合，所以它很好地描述了计算机科学离散性的特点［1－5］.离散数学作为计算机科学领域最有效的一种数学工具，从70年代初，国外就已经作为一门课程正式列入计算机科学和一些工程学系的教学计划中.

数学是揭示事物数量与形体本质联系的学科，教学中可以挖掘出的幽默元素是很多的，一个形象巧妙的比喻，一个十分贴切的类比，既能反映数学概念方法的简单直观，又将生活中形象的现象与枯燥抽象的数学联系起来，其中的含义回味悠长，产生出雅致的数学幽默［6－14］.作者主要探讨离散数学中一些显性闭包概念、隐性闭包概念及针对它们的教学方法设计.最后介绍了传递闭包的算法及相关应用.

1 离散数学中显性的闭包概念

1.1 二元关系的闭包

在离散数学中，关系理论是其一个重要的组成部分，它的知识点主要包括关系的性质、关系的复合、逆运算和闭包运算、关系的划分和覆盖，以及等价关系、相容关系、序关系几种特殊的关系.可以通过求关系的传递闭包来实现传递性的判断，而传递闭包本身在图论中有很好的应用价值.所以二元关系闭包是一个重要的概念，在计算机科学中有着广泛的应用.

关系的闭包是计算机专业本科生第一次正式接触闭包的概念，几乎所有的教材资料都是这样定义的［1－4］.

定义1：设R是集合A上二元关系，称R′为R的自反闭包（对称闭包，传递闭包），如果R′满足：

（1）R′是自反的（对称的，传递的）；

（3）对A上任意关系R″，若R″满足上面的条件（1）和（2），则

一个关系R的自反闭包、对称闭包和传递闭包分别记作r（R）、s（R）、t（R），也称r，s，t为闭包运算（算子），它们作用于关系R后，分别产生包含R的最小的自反关系、对称关系和传递关系.

首先介绍凸平面区域及凸几何体的概念.通过画几个图，举几个生活中的例子，学生就可以判断一个平面区域或几何体是不是凸的，但是它们的数学定义又是怎样的呢？

定义2：任意选取区域内的两个点，它们的连线也在区域内，则该区域就是一个凸的区域.

在定义2的基础上再引出一个区域的凸闭包的概念：如果一个区域D不是凸的，适当放大后的区域D’是凸的，且少放大一点都不是凸的，即D’是包含D的最小凸区域，称之为原来区域D的凸闭包.

关系闭包的基本思想：假设关系R不具有性质P，可以在R中添加一些二元序对，使之具有性质P，并希望添加的二元序对尽可能的少.举例如下：

例1：设R＝ ｛（a，a），（a，c），（c，b）｝是集合A＝ ｛a，b，c｝上的一个二元关系，且不是自反、对称、传递的.将R适当放大，添加最少的序对，使之分别满足自反、对称、传递性.

和同学一起寻找到以下结果：

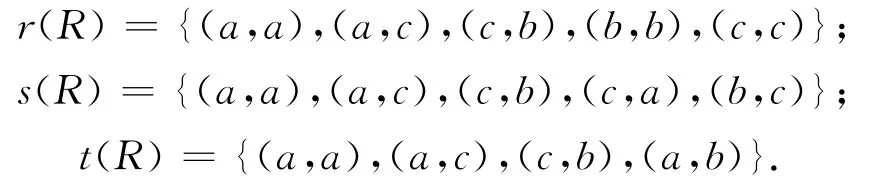
之后再介绍二元关系的闭包定义1.

1.2 无向图的闭包

图论中关于一个图的闭包概念［1］描述如下：

定义3：给定无向图G＝＜V，E＞，｜V｜＝n，图G的闭包是由G通过相继地用边连接两个其度数之和至少为n的不邻接的结点，直到不能如此进行为止而得到的图，称为图G的闭包C（G）.

在这个定义中，是在不增加点的前提下，将图G适当放大，对u，v∈V，u与v间没有边关联，依据条件deg（u）＋deg（v）≥n，就将边（u，v）添加进去，直至没有边可以加入为止.即是在满足条件下可以加入G的最多的边后得到闭包C（G）.课堂上给同学们举个例子示范一下，如下图1，以帮助理解.

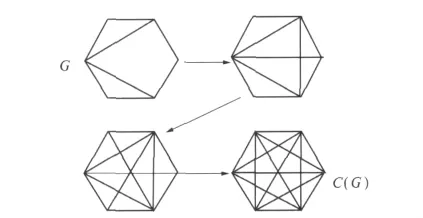
图1 图的闭包生成过程Fig.1 The closure of graph gener ating process

2 离散数学中隐式的闭包概念

所谓隐式的闭包概念，我们指的是那些没有直接说明是什么的闭包，但是这些概念具有闭包特性.闭包的特性是适当放大，且是满足某性质（条件）的最小的对象集合.

2.1 线性代数中的隐性闭包概念

在线性代数中有关于和空间和生成子空间的概念［6］，并有以下的结论.

其实结论1中两个子空间的和空间，本质上就是包含U和W的最小子空间，即具有闭包的特性：集合U∪W 一般情况下不是Rn的子空间，将U∪W 适当放大，使之成为Rn的子空间，且是最小的（添加元素最少的）.课堂上可以给个这样的例子：在二维平面R2上，U，W分别是过原点的两条直线，那么它们都是R2的子空间，但是U∪W不是R2的子空间，除非U，W 是同一条直线.此时U＋W 又是什么呢？可以通过向量的加法运算，即同学们在中学就熟悉的平行四边形的对角线法，说明这样的向量可以是R2中的任意一个向量，从而得到U＋W ＝R2.

结 论 2：设 α1，α2，…，αs∈ Rn，则 集 合2，…，s｝是Rn的子空间，并称为是由向量α1，α2，…，αs生成的子空间.

其实结论2中的span（α1，α2，…，αs）就相当于集合 ｛α1，α2，…，αs｝关于子空间这个性质的闭包，因为span（α1，α2，…，αs）就是包含 ｛α1，α2，…，αs｝的最小子空间。例如R2中的两个向量e1＝（1，0）T，e2＝ （0，1）T，则由它们两个向量生成的子空间span（e1，e2）＝R2.

2.2 图论中的隐性闭包概念

图论［1－4］中这样的概念比较多，我们在这里只是介绍几个比较难理解的概念，针对这些概念，我们用闭包的思想和构造操作，以“相对直观”的意义，用深入浅出的方法讲授，达到帮助同学们对概念的归类掌握和理解.

连通分支：设G＝＜V，E＞是一个无向图，称G的子图G1是G的一个连通分支，如果G1是连通的，且是满足连通性的最大子图.

事实上这个概念就是将G的连通子图放大，放大到一个临界状态，当前的子图是连通的，再放大就不连通了.这个就是包含初始连通子图的最大连通子图，即为一个连通分支.显然连通分支的概念是具有闭包特性的，这样解释后就很容易通过例子帮助学生掌握连通分支的概念及怎么找一个无向图的连通分支.

强分图（单向分图、弱分图）：设G＝＜V，E＞ 是一个有向图，G1＝ （V1，E1）是G的子图，如果G1是强连通图（单向连通图、弱连通图），且没有包含G1的更大的子图是强连通图（单向连通图、弱连通图），则称G1是G的强分图（单向分图、弱分图）.

这3个概念都具有闭包的特性，就是要将G的强连通（单向连通、弱连通）子图进行放大，放大到一个临界状态，当前的子图是强连通（单向连通、弱连通）的，再放大就不是强连通（单向连通、弱连通）了.找到的这个子图就是包含初始强连通（单向连通、弱连通）子图的最大强连通（单向连通、弱连通）子图.如此分析了概念，然后再构造三个有向图：1）一个不是强连通但是单向连通的；2）一个不是单向连通但是弱连通的；3）一个不是弱连通的.和同学们一起按照上面闭包的特性去寻找强分图（单向分图、弱分图）.

点（边）割集：设G＝＜V，E＞是一个无向连通图，对V1⊆V（E1⊆E），G－V1（G－E1）是不连通的图，且对任意的V2⊆V1（E2⊆E1），GV2（G－E2）是连通的图，则称V1（E1）是图G的一个点（边）割集.

在这两个概念里，点割集就是使连通图G变成不连通图需要删除的极大点集，少一个点还是连通的；边割集就是使连通图G变成不连通图需要删除的极大边集，少一条边还是连通的.按照这个思想，通过实例图形与同学一起寻找点割集、边割集，并且自然会发现一个图的点割集、边割集不是唯一的，所含的点（边）数也可以不同，从而很自然地就可以引出一个连通图的点连通度及边连通度的概念.

我们发现用闭包的特性来分析、讲解这些概念，就为同学们理解这一类的概念找到一个几乎统一的格式，不仅使概念变得容易理解，且找到了可以实现的操作方法和途径.

2.3 代数系统中的隐性闭包概念

代数系统及其子系统都有生成的概念，群、环、域、模和格等都一样［8］.通过一些对象元素生成满足相关条件的子系统，这些概念的教学都可以借助闭包的特性来类比.下面以群和域中的几个概念的处理为例.

定义4 （生成子群）［2］：设 （G，·）是一个群，B是群G的非空子集，将G的所有包含B的子群的交记作＜B＞，即：

从生成子群的定义可以看出，＜B＞是G中包含B的最小子群，显然具有闭包的特性。其实我们可以证明，＜B＞中元素恰好为形式：其中ai是B 中的元素或其逆元，Z＋是正整数的集合.即对集合B添加所有这种形式的元素就可以得到闭包（生成子群）＜B＞.特别地，如果B只含一个元素b，那么＜B＞称为是循环子群，由元素b生成的循环子群，并简记为＜b＞.例如对于整数加群，由2生成的子群是＋6）中，由2生成的子群是 ＜2＞＝ ｛0，2，4｝.

利用生成子群的思想及拉格朗日定理，我们就可以与同学们一起求解一些熟悉的有限群的全部子群.如可以求得（ℤ8，＋8）的非平凡子群有两个，（ℤ12，＋12）的非平凡子群有四个等等.

其他的生成子代数也同样具有闭包特性的，如生成子半群、生成子环、生成理想、生成子域等等.比如我们讲到域的定义之后，会与学生说有理数域Q、实数域R、复数域C都是符合这个定义的，并给出数域的定义.复数域C的子域称为数域，让同学们试试找出其他数域的例子，给学生一定的提示引导学生验证如都是数域.最后证明有理数域Q是最小的数域，这时要同学体会从集合｛0，1｝出发逐步生成数域的过程，｛0，1｝→N→Z→Q.

3 抽象数学中的闭包概念及闭包算子

在数学中，一个集合被称为在某个运算下闭合，如果在这个集合的成员上的运算生成这个集合的成员.例如，实数在减法下闭合，但自然数不行，自然数3和7的减法3－7的结果不是自然数.类似的，一个集合被称为在某些运算的下是闭合，如果它单独的闭合在每个运算之下.

当一个集合S不闭合在某个（些）运算下的时候，我们通常可以找到包含S的最小的闭合集合.这个最小闭合集合被称为S的关于这个（些）运算的闭包.例如，在自然数集的减法下的闭包，被看作实数的子集，是整数集.

关于某个运算的集合的闭包定义了在X的子集上的闭包算子.闭合集合可以确定自闭包算子；一个集合是闭合的，如果它等于自己的闭包.所有闭包算子的典型结构性特征是：

（1）闭包是递增的或扩大的：一个对象的闭包包含这个对象.

（2）闭包是幂等的：闭包的闭包等于闭包.

（3）闭包是单调的：就是说，如果X包含在Y中，则C（X）也包含在C（Y）.这三个性质可以看做抽象闭包算子的定义.

4 无向图传递闭包的应用

无向图的传递闭包主要用于判断图的连通性和图中满足条件的连通分支，具有很高的实用价值［3，8］.借鉴无向图的传递闭包的思想，可以计算图中每一对顶点之间的最短路径（实际上就是Fl oyd算法的思想）.

4.1 计算一对顶点间的最短路径（floyd算法）

现有一张城市地图，图中的顶点为城市，有向边代表两个城市间的连通关系，边上的权即为距离.现在的问题是，为每一对可达的城市间设计一条公共汽车线路，要求线路的长度在所有可能的方案里是最短的.

以下e行，每行为边（i，j）和该边的距离wij

输出：k行，每行为一条公共汽车线路.

在枚举途径某中间顶点k的任两个顶点对i和j时，将顶点i和顶点j中间加入顶点k后是否连通的判断，改为顶点i途径顶点k至顶点j的路径是否为顶点i至顶点j的最短路径（1≤i，j，k≤n）.显然三重循环即可计算出任一对顶点间的最短路径.设n是有向图的结点个数；path是最短路径集合.其中path［i，j］为vi至vj的最短路上vj的前趋结点序号（1≤i，j≤n）；adj是最短路径矩阵.初始时为有向图的相邻矩阵，用类似传递闭包的计算方法反复对adj矩阵进行运算，最后使得adj成为存储每一对顶点间的最短路径的矩阵.

4.2 应用举例

问题一：判断无向图中任意两个顶点之间是否有路.

例2：输入一张无向图，指出该图中哪些顶点对之间有路.

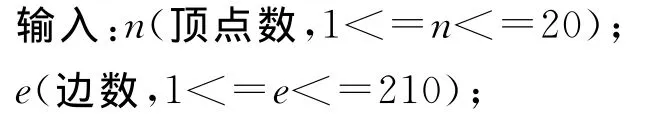
以下e行，每行为有边连接的一对顶点.

输出：k行，每行两个数，为存在路的顶点对序号i，j，要求i＜j.

一般采用宽度优先或深度优先遍历来解决.因为从任意一个顶点出发，进行一次遍历，就可以求出此顶点和其它各个顶点的连通状况.所以只要把每个顶点作为出发点都进行一次遍历，就能知道任意两个顶点之间是否有路存在.一次遍历的时间复杂度为O（n），要穷举每个顶点，所以总的时间复杂度为O（n＊n）.

问题二：寻找满足条件的连通分支 .

例3：输入一张顶点带权的无向图，分别计算含顶点数最多的一个连通分支和顶点的权之和最大的一个连通分支.

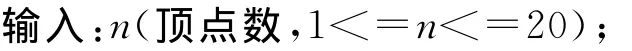
以下n行，依次表示顶点1到顶点n上的权；

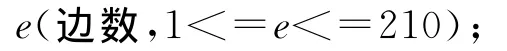
以下e行，每行为有边连接的一对顶点.

输出：两行，一行为含顶点数最多的一个连通分支，一行为顶点的权之和最大的一个连通分支，输出时按顶点编号从小到大输出.

例4：一笔画问题

问题描述：编程对给定的一个图，判断能否一笔画出，若能请输出一笔画的先后顺序，否则输出“No Solution！”.

输入：输入文件共n＋1行，第1行为图的顶点数n，接下来的n行（每行n个数据）为图的邻接矩阵，G［i，j］＝1表示顶点i和顶点j有边相连，G［i，j］＝0表示顶点i和顶点j无边相连.

输出：若能一笔画出，则输出一笔画出的顶点先后顺序，否则输出“No Sol ution！”.

样例输入：

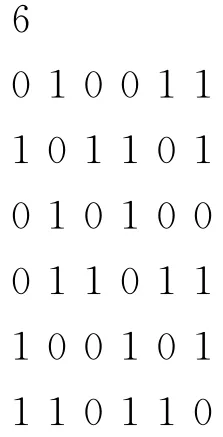
样例输出：

5 结束语

作者从闭包的特性出发，整理了一组离散数学中具有闭包特性的概念，引导学生有效的进行归类学习，理解所学知识的思路、方法和技巧，并通过应用实例提高同学们应用知识的能力.在教学中要重视概念教学，从概念的产生、发展、内涵和与其它相关知识的联系，整个来龙去脉，用学生浅显易懂的方式讲授，循序渐进地让学生接受这些难以理解的概念及思想方法.

［1］ 左孝凌，李为监，刘永才.离散数学［M］.上海：上海科技文献出版社，2001.

［2］ 耿素云，屈婉玲，张立昂.离散数学［M］.北京：高等教育出版社，2008.

［3］ 傅彦.离散数学基础及应用［M］.成都：电子科技大学出版社.2000.

［4］ 孙吉贵，杨风杰，欧阳丹彤，等.离散数学［M］.北京：高等教育出版社.2002.

［5］ KENNET H A R，CHARLES R B.Discrete Mathematics（Fifth Edition）［M］.北京：清华大学出版社，2003.

［6］ 吴明芬，汪立民.代数系统中的数学思想及同构（同态）的初等诠释［J］.计算机科学，2010，37（7），15－19.

［7］ 许蔓苓.离散数学的方法与挑战［J］.计算机研究与发展.2002，39（12）：1771－1772.

［8］ 李梅霞.离散数学中关系性质的判定方法［J］.大学数学，2010，26（5）203－206.

［9］ 李小梅.“离散数学”中代数理论教学的处置［J］.赣南师范学院学报.2000（3）：75－76.

［10］崔艳荣，陈勇，黄艳娟.离散数学教学方法与手段探［J］.长江大学学报，2009，6（2）：373－374.

［11］薛占熬，肖运花，杜浩翠，等.论 “双主"在离散数学教学过程中的作用［J］.计算机教育，2011，18：37－40.

［12］刘卫锋，刘 林，王东晓，等.数学文化融入离散数学的教学研究［J］.计算机教育，2011（6）：52－55.

［13］吴明芬，张先勇.应用驱动激发离散数学课程的学习兴趣和动力［C］.大学计算机课程报告论坛论文集.北京：高等教育出版社，2009：281－285.

［14］朱家义，苗国义，梁云娟.基于知识关系的离散数学教学内容设计［J］.计算机教育，2010（18）：98－100.