非平稳路面激励下车辆振动动力学建模与仿真

胡启国，钱 凯，李力克，岳光杰，司红建

(重庆交通大学机电与汽车工程学院，重庆400074)

0 引言

来自路面的随机激励会引起汽车的振动，这种振动将会影响汽车的乘坐舒适性，所以研究汽车的振动特性是很有必要的［1］.目前车辆平顺性分析研究的前提是车辆在匀速的情况下行驶.这种方法在一定程度上反映了车辆行驶的振动特性，但研究结果不能客观真实地反映实际的振动特性.为了研究驾驶员在汽车匀加速过程中的振动情况，建立了非平稳路面激励模型，并以此作为汽车前后轮的输入，建立1/2车身五自由度的非匀速行驶的车辆振动模型，研究路面不平度等级、汽车加速度、汽车悬架系统参数、座椅悬架系统参数对驾驶员乘坐舒适性的影响.

1 路面模型的建立

路面不平度主要用路面功率谱密度描述其统计特性.路面功率谱密度可以表示为［2］

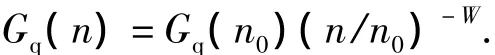
式中:n为空间频率，m-1;n0=0.1 m-1为参考空间频率，Gq(n0)为参考空间频率n0下的路面功率谱密度值，称为路面不平度系数，单位为m2/m-1=m3;W为频率指数，它决定路面功率谱密度的频率结构，一般近似取值为2.根据路面功率谱密度把路面等级分为8级，表1给出了4级路面的相关参数.

表1 路面不平度分类标准Tab.1 Roughness of road surface of rank standard

汽车在非匀速行驶时，汽车前轮受到的路面激励可以表示为［3］

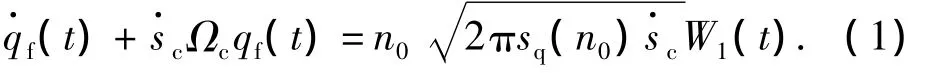
由于汽车前后轮存在着迟滞性，所以汽车前后轮激励可以表示为

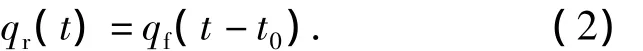
通过式(1)和式(2)可以将汽车后轮受到的路面激励表示为式(3):

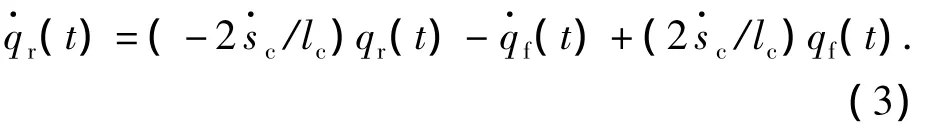
式中:qf(t)、qr(t)分别为汽车前后轮的路面激励的时域表达式;sc为汽车前轮的水平位移;Ωc=2πnc为路面空间截止角频率;W1(t)是平稳白噪声;lc=c+d为轴距.

由式(1)与(3)并通过MATLAB/simulink模块对初速度为0 m/s、加速度为3 m/s2，C级路面，汽车轴距为2.5 m，汽车加速行驶15 s，进行建模，仿真结果见图1～2.

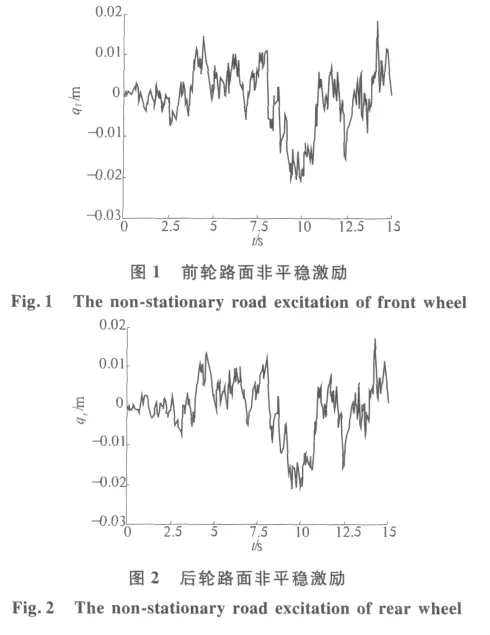
通过图1～2可知，在0～5 s内，随着车速的增加，汽车前后轮受到路面激励振幅较小，即车速在15 m/s以内，汽车受到地面冲击相对较小.但随着加速时间的增加，汽车受到的路面激励幅值也在增加.但当车速增加到一定的程度，路面的激励幅值基本上在一个稳定的范围内上下波动.

2 非平稳激励的时频分析

采用伪Margenau-Hill时频分析对前后轮路面激励进行时频分析［4］.假设路面激励信号x(t)的时频分布p(t，f)一般形式为:

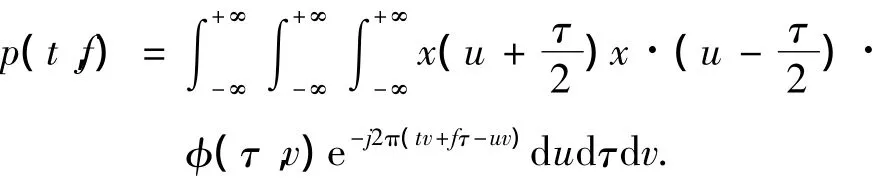
式中:φ(τ，v)是核函数.当φ≡cos(πτv)，并且对变量τ加窗函数 h(τ)，此时该分布称之为伪Margenau-Hill分布，可表示为:

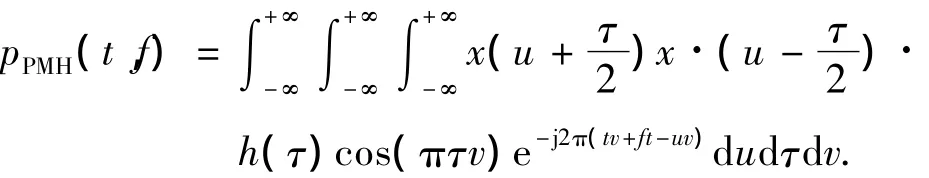
其中，h(τ)为窗函数.

图3(a)、(b)为前后轮伪Margenau-Hill时频分布图.路面激励瞬态信号在整个时频中呈现出低频信号，在时频图谱中体现出能量的集中.结合图1～3可以将路面低频波动特征表征出来.

图3 前轮和后轮Margenau-Hill时频分布Fig.3 The front and rear wheel of the Margenau-Hill time-frequency distribution

3 五自由度汽车振动模型的建立

为研究非平稳路面激励下车辆的振动特性，将汽车简化为二分之一车身的五自由度振动模型，模型见图4:mz为汽车座椅质量;Zc为座椅位移;Kz为座椅底座刚度;Cz为座椅底座阻尼系数;mb为簧载质量;Zb为簧载质量质心位移;θb为车身的俯仰转角;Ip为车身转动惯量;Z2、Z4为前后轴对应的车身垂直位移;Ksf、Ksr为前后悬架弹簧刚度;Csf、Csr为前后轴阻尼系数;Z1、Z3为前后轮垂直位移;mwf、mwr为前后轮胎质量;Ktf、Ktr为前后轮胎阻尼系数;qf、qr为前后轮路面激励.

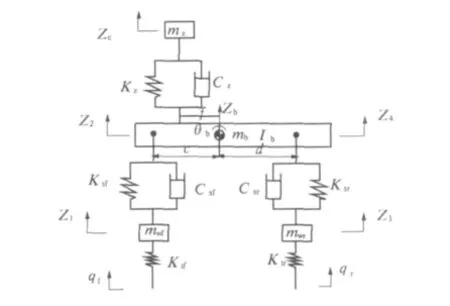
图4 五自由度汽车动力学模型Fig.4 Five DOE dynamics model of the vehicle

根据第二类拉格郎日方程对五自由度汽车振动动力学模型建立微分方程，其拉格朗日方程的形式［5-9］:式中:T为系统动能;U为系统势能;D为系统耗散能;Qi为广义激振力.

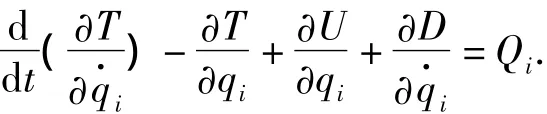
系统的广义坐标为:AT= ［Z1，Z3，Zb，Zc，θb］;

系统的动能方程为:

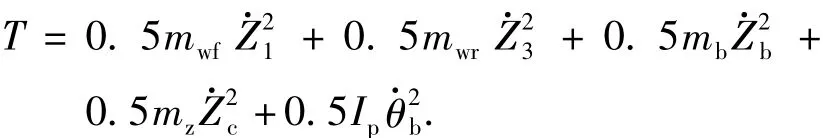
系统的势能方程:

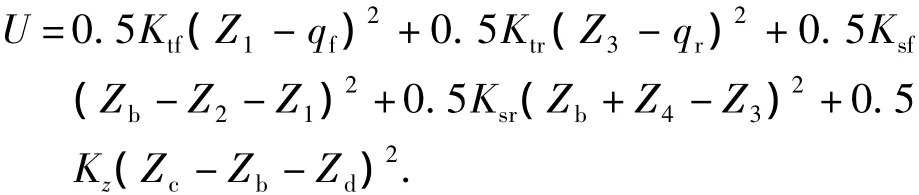
式中:Z2=cθb;Z4=dθb;Zd=fθb.

系统的耗能方程:

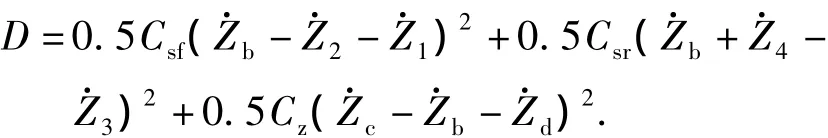
根据系统的动能方程、势能方程、耗能方程，将上述方程简写为:

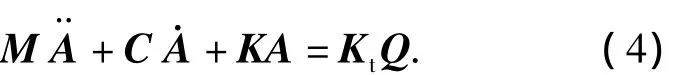
其中，

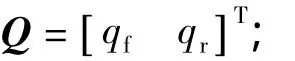
将方程式(4)转化为状态方程，最终的形式为

4 仿真参数确定与模型建立

某车辆的基本参数如表2所示.根据表2的汽车参数和振动动力学方程(5)，运用MATLAB/simulink建立五自由度汽车振动动力学模型，如图5所示.

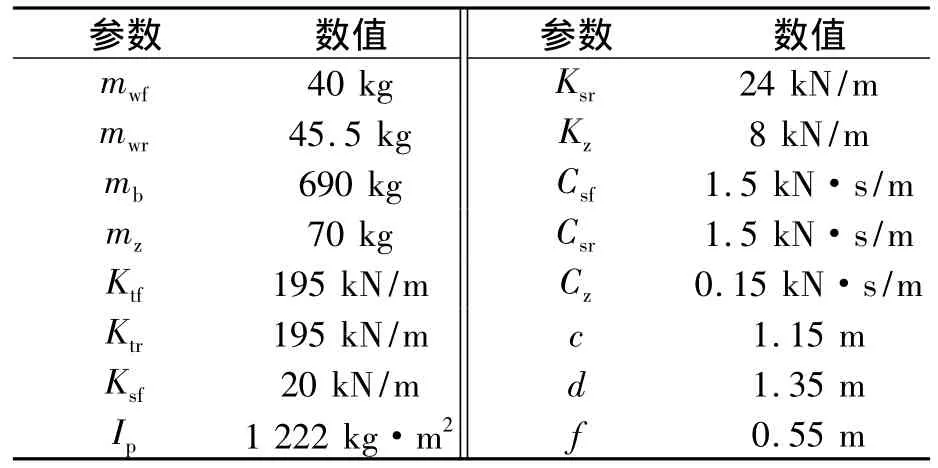
表2 汽车基本参数Tab.2 Basic parameters of vehicle

图5 五自由度汽车动力学simulink模型Fig.5 Five DOE dynamics model of the vehicle

5 仿真分析

5.1 车辆加速度对座椅垂直振动加速度的影响

汽车以初速度为0 m/s，加速度分别为2，3，4 m/s2，加速行驶377.5 m，座椅振动加速度曲线见图6.在整个加速过程中，加速度越大，座椅垂直振动加速度的幅值也相应较大.这说明汽车加速度对人的乘坐舒适性有很大的影响.

5.2 路面不平度对座椅垂直加速度的影响

在B、C、D级3种路面上以相同的加速度加速行驶15 s，座椅的振动垂直振动加速度最大分别为1.52，3.06，6.13 m/s2.路面不平度对座椅垂直加速度的影响如图7所示.可见路面的好坏程度直接影响到座椅的垂直振动加速度，从而影响人的乘坐舒适性.

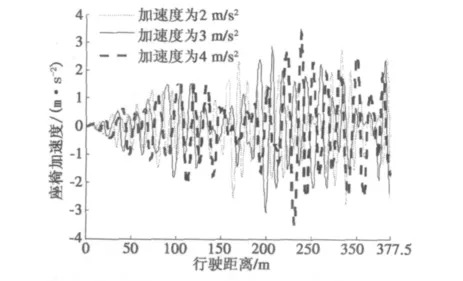
图6 不同加速度下座椅垂直振动加速度曲线Fig.6 The seat of the vehicle vertical acceleration curve on different

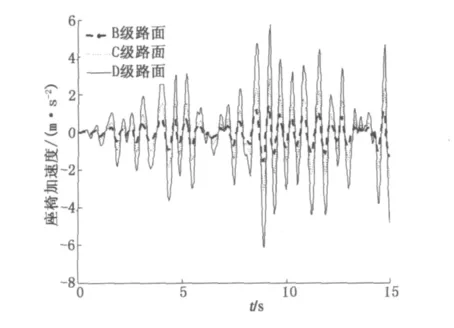
图7 不同等级路下座椅振动加速度曲线Fig.7 The seat of the vehicle vertical acceleration curve on different road

5.3 座椅刚度与阻尼对座椅加速度的影响

汽车以初速度为0 m/s，加速度为2 m/s2，在D级路面，分别将座椅悬架系统的刚度与阻尼改变为原来的50%、100%、150%，仿真分析结果见图8.图8(a)表明减小座椅刚度可以降低汽车座椅处的振动加速度;图8(b)说明增加阻尼降低了座椅处的振动加速度.

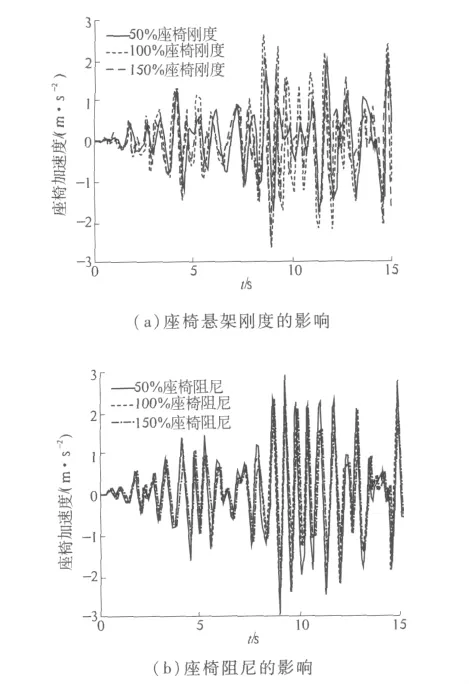
图8 座椅阻尼和座椅悬架刚度对座椅振动加速度Fig.8 Influence of suspension stiffness and damping of seat on acceleration of seat

5.4 前悬架刚度和阻尼对座椅振动加速度影响

将前悬架刚度与阻尼分别改变为原来的50%、100%、150%，仿真分析结果见图9.

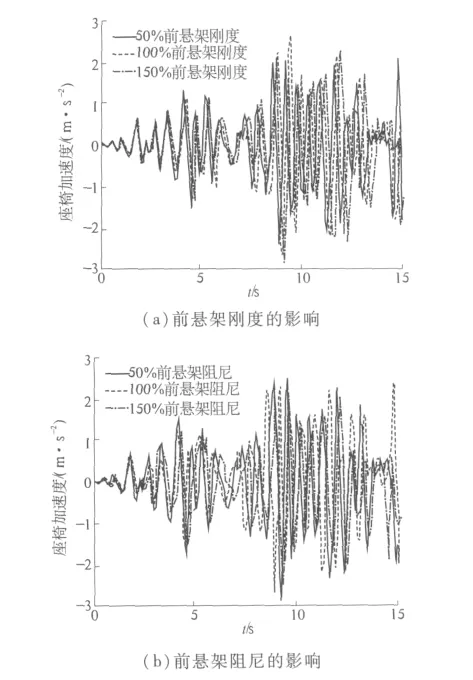
图9 前悬架刚度和阻尼对座椅振动加速度的影响Fig.9 Influence of front suspension stiffness and damping on acceleration of the seat

图9 (a)表明改变前悬架刚度，座椅处振动加速度幅值没有发生明显的改变.图9(b)说明了改变前悬架阻尼对座椅振动变化影响不大.

5.5 后悬架刚度和阻尼对座椅振动加速度影响

将后悬架刚度与阻尼分别改变为原来的50%、100%、150%，仿真分析结果见图10.

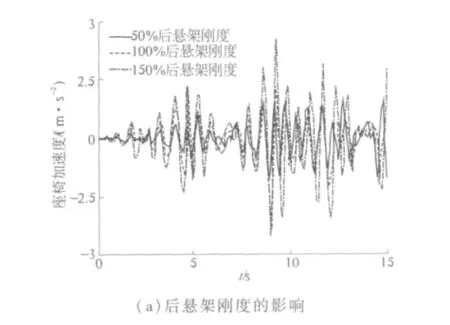
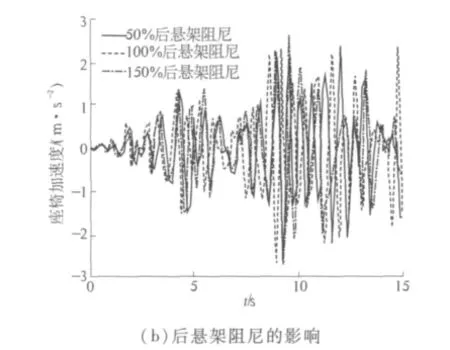
图10 后悬架刚度和阻尼对座椅振动加速度的影响Fig.10 Influence of rear suspension stiffness and damping on acceleration of the seat

图10 (a)显示后悬架刚度增加或减小50%时，座椅处振动加速度幅值发生了较大的变化;图10(b)也说明了改变后悬架阻尼对座椅振动变化影响没有改变刚度那么明显，但增大后悬架阻尼可以在一定程度上减小座椅处的振动加速度幅值.

6 结论

(1)建立了非平稳激励路面，运用伪Margenau-Hill时频分析方法对非平稳路面信号进行时频分析，分析结果表明随着车速的增加，路面低频成分在增加，体现出了路面的低频波动性.

(2)通过MATLAB/simulink建立5自由度的非平稳路面激励的汽车振动动力学模型，通过仿真模拟分析得出:在相同等级的路面上，加速度越大，座椅处垂直的振动加速度越大;在同一加速条件下，路面状况越差，座椅处垂直振动加速度越大.

(3)在满足座椅悬架系统参数的条件下，适当的降低座椅悬架刚度与提高阻尼可以提高驾驶员的乘坐舒适性.对于前悬架系统，降低刚度与增加阻尼对提高乘坐舒适性效果不佳.但是适当的降低后悬架系统的刚度，增加阻尼，可以提高驾驶员的乘坐舒适性.

［1］ 宋一凡，陈荣峰，梁乃兴.基于路面不平整度的车辆振动响应分析方法［J］.交通运输工程学报，2007，7(4):39-43.

［2］ 余志生.汽车理论［M］.北京:机械工业出版社，2006.

［3］ 张立军，张天侠.车辆非匀速行驶时路面随机输入的时频研究［J］.汽车工程，2005，27(6):710-714.

［4］ 刘日龙，冯志华.Margenau-Hill分布在滚动轴承故障识别中的应用［J］.振动与冲击，2006，25(2):175-177.

［5］ 勒晓雄，张立军，江浩.汽车振动分析［M］.上海:同济大学出版社，2002.

［6］ 黄志刚，毛恩荣，梁新成，朱慧.微型轿车八自由度整车动力学仿真与试验［J］.农业机械学报，2008，39(6):29-33.

［7］ 王连明，宋宝玉，周岩，郑胜军.汽车平顺性建模及其仿真研究［J］.哈尔滨工业大学学报，1998，30(5):80-84.

［8］ 张鄂，刘中华，邵晓春.九自由度乘坐动力学模型的人体振动特性仿真［J］.交通运输工程学报，2010，10(4):58-64.

［9］ 张洪亮，杨万桥.基于人-车-路五自由度振动模型的路面不平整度评价方法［J］.交通运输工程学报，2010，10(4):16-22.