基于矢量曲面积分反演模型的舰船磁场延拓方法
张朝阳,衣 军
(中国人民解放军91872 部队,上海200083)
0 引 言
舰船消磁是提高舰船磁性防护能力的有效手段[1],而评估舰船磁性防护能力往往是通过一定深度(或高度)上某些点的磁场来进行的。但在实际中,受测量条件(如水深、高度等)的限制,往往很难直接测量到所需目标深度(或高度)的磁场,需要通过已知测量点的磁场延拓计算得到。
目前常见的可用于舰船磁场计算的方法有:有限元法[2-3]、积分方程法[4]和磁体模拟法。有限元法需要对磁体进行复杂的剖分,并且需要知道磁体的磁性参数,其计算精度受剖分好坏的影响。同时,有限元法的计算量非常大,耗时很长。积分方程法和有限元法一样,有着运算复杂、费时的缺陷。磁体模拟法[5-6]中常用磁偶极子或旋转椭球体作为模拟体,其换算精度受人为经验的影响较大,稳定性和精度也难以保证。随着磁场计算技术的进步,近年来在舰船磁场计算领域,出现了一种简便快捷的矢量曲面积分法[7],可以通过测量舰船包络面的三分量磁场准确快速地延拓得到舰船任意深度上的磁场。但该方法需要测量包络面的三分量磁场,而在通常情况下,只能得到舰船下方某个平面的磁场。本文试图通过舰船下方某平面的测量磁场,建立舰船磁场的矢量曲面积分反演模型,从而实现舰船磁场的延拓推算。
1 舰船磁场的矢量曲面积分延拓模型
设场域为V,内边界面为S,如图1所示。场域内的磁源可等效为自由电流,其分布密度为J 矢量。场域内介质均匀且各向同性,则在场域内磁场的特性可以用向量磁位A 描述,有:
∇× A=B,∇× ∇× A=μJ。
式中:B 为磁感应强度矢量;μ 为介质磁导率;J(x′,y′,z′)为场域内自由电流密度向量或铁磁物体的等效电流密度向量。选取格林函数

将格林函数和向量磁位A 代入格林第一恒等式和格林第二恒等式[8]进行一系列矢量运算后可以得到表达式[7]

式(1)即为场域V 内P 点磁场的矢量曲面积分计算公式。
由于铁磁物体外的空间(V)内一般不存在自由电流或铁磁物质,因此式(1)可简化为
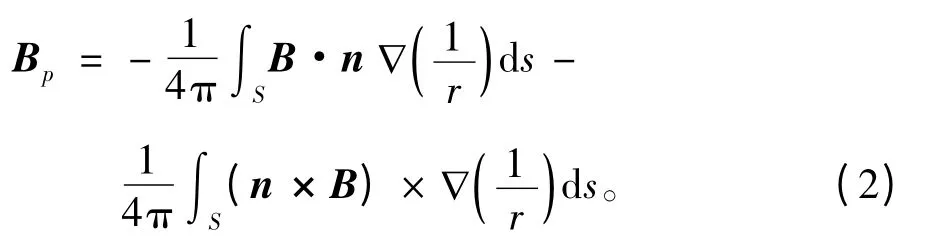
式(2)即为常用的铁磁物体磁场矢量曲面积分延拓公式[7]。其物理意义为:铁磁物体(如舰船)周围空间任意点的磁感应强度矢量可以通过包围铁磁物体的封闭曲面上的磁感应强度矢量的面积分得到。
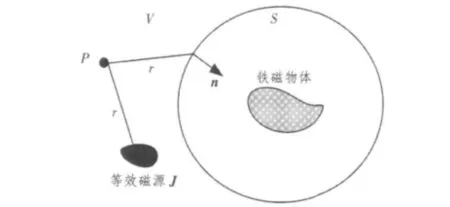
图1 矢量曲面积分示意图Fig.1 The sketch map of vector surface integral
利用式(2),只要获得了舰船包络面上的矢量磁场,即可计算出周围空间任意点的矢量磁场。
2 基于矢量曲面积分反演模型的磁场延拓
在利用式(2)进行磁场延拓时,一般要根据磁场测量的实际情况,对包络面进行单元剖分,每个测量点为1 个剖分单元,然后在包络面上进行数值积分得到空间磁场。设空间磁场向量用b 表示,则空间磁场的数值积分关系可简化表示为

式中:x 为包络面磁场向量;K 为数值积分所形成的观测矩阵。
在舰船磁场的实际测量中,除特殊场站外,包络面磁场一般很难得到,往往只能获得下方某个深度的磁场,若将测量得到的磁场记作向量b1,同时设定舰船周围包络面并作一定剖分(由测量深度得到K),则可对式(3)求逆,得到等效包络面磁场x;再利用式(3)延拓得到目标深度上的磁场b2。
由测量平面磁场反演得到舰船等效包络面磁场再计算目标深度磁场的过程如图2所示。
在反演求解方程(3)时,要注意等效包络面的剖分数一定不能大于平面磁场的测量点数。另外,在方程求解时,系数矩阵K 的条件数有时很大,这时需要通过奇异值分解或正则化处理[9]得到方程的稳定解。
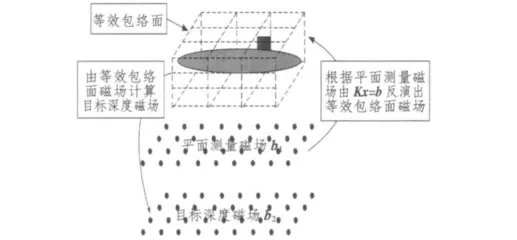
图2 反演计算目标磁场示意图Fig.2 The sketch map for the inverse calculation of objective magnetic field
3 船模实验
以1 个长308 cm,宽30.8 cm 的铁质结构船模为实验对象,用三分量磁通门传感器阵列测量船模磁场。按照图2 中所示,分别测量船模下方2 个深度的磁场(b1和b2)。b1对应的测量深度为h1=61 cm,测量范围为12 m ×1.2 m(61 ×7 的阵列,间隔0.2 m);b2对应的测量深度为h2=90 cm,测量范围为12 m×0.8 m(61 ×5 的阵列,间隔0.2 m)。船模的中心在测量平面上的投影与平面中心重合。船模的等效包络面长为12 m,取纵向的4 个矩形面(由于2 端磁场接近零,忽略端面)进行剖分,共分为160个单元。用h1深度上的磁场b1计算船模包络面的等效磁场,然后由反演模型延拓计算h2深度的磁场,并与测量值进行比较,考察磁场延拓的精度。
定义计算的相对均方根误差为

式中:Bm和Bc分别为磁场的测量值和延拓计算值;为相应测量值的最大值;N 为测量点数。
表1 为h2深度上磁场三分量的延拓均方根误差,从表中可以看出,利用矢量曲面积分的反演模型能准确延拓计算其他深度上的磁场。差则会变得很大。主要原因是:计算近场磁场的线性方程组Kx=b 的系数矩阵K 的条件数虽然较大(可达107以上),但通过一定的方法处理,可以求得一个稳定的解,在换算距离不大时,磁场换算的误差不会很大;但当距离舰船较远时,其系数矩阵条件数可以达到1017以上,如果求出的等效包络面磁场与实际磁场有所差异,则可能引起很大的计算误差。

表1 h2深度上三分量磁场的均方根误差Tab.1 The average square root errors of the 3 components field at h2depth

图3 x 分量计算值与测量值比较Fig.3 The compare of calculated value and measured value for x component


图3 ~图5 分别为x,y,z 三个分量某条测量线上计算值与测量值的比较情况。其中,Bx-m 表示测量值,Bx-c 表示计算值,其余分量类推。从图中可以看出,通过反演船模的等效包络面磁场,然后延拓计算其他深度的磁场是可行的,能保证一定的计算精度。
另外,通过大量实验计算可以得到,利用矢量曲面积分的反演模型延拓计算磁场的方法在较近换算深度上是准确地,当距离舰船较远时,其计算误
4 结 语
根据舰船磁场的矢量曲面积分延拓方法,由已知深度上的平面磁场反演出舰船的等效包络面磁场,进而延拓计算出目标深度上的磁场,船模实验表明了该方法的可行性,其延拓计算的均方根误差可控制在5%以内。该方法相比磁体模拟法、有限元法等而言,无需人为经验和复杂运算,方法更为简单有效,非常适合舰船近场磁场的延拓计算,为舰船磁隐身技术中的磁场换算提供了一种思路,具有较好的实际应用价值。
[1]张连魁.舰船磁场分析-临时线圈消磁[M].武汉:海军工程大学,1991.
[2]STABLIK M J,RUBIN S W,JILES D C,et al.Finite element simulation of magnetic detection of creep damage at seam welds[J].IEEE Transactions on Magnetics,1996,32(5):4290-4292.
[3]GORDON J C A.Modelling the induced magnetic signature of naval vessels[D].England:Department of Physics and Astronomy University of Glasgow,2000.
[4]郭成豹,何明,周耀忠.积分方程法计算舰船感应磁场[J].海军工程大学学报,2001,6(13):71-74.
GUO Cheng-bao,HE Ming,ZHOU Yao-zhong.Calculation of induced magnetic fields of ships by integral equation method[J].Journal of Naval University of Engineering,2001,6(13):71-74.
[5]周耀忠,张国友.舰船磁场分析计算[M].北京:国防工业出版社,2004.
[6]阎毓杰,樊友文,杨华荣.基于磁体模拟法的舰船磁场补偿技术[J].舰船科学技术,2009,31(5):82-86.
YAN Yu-jie,FAN You-wen,YANG Hua-rong.A magnetic field compensating method based on the magnet simulation theory for vessel[J].Ship Science and Technology,2009,31(5):82-86.
[7]闫辉,肖昌汉,周国华.基于曲面积分的磁场矢量延拓方法[J].兵工学报,2008,29(7):839-843.
YAN Hui,XIAO Chang-han,ZHOU Guo-hua.Continuation of magnetic vector based on a surface integral technique[J].Acta Armamentarii,2008,29(7):839-843.
[8]樊明武,颜威利.电磁场积分方程法[M].北京:机械工业出版社,1988.
[9]ENGL H W.Discrepancy principles for Tikhonov regularization of ill-posed problems leading to optimal convergence rates[J].J Optim Theory Appl,1987,52:209-215.

