玻璃纤维增强PA66复合材料非等温结晶动力学的研究
陈 坤,郑梯和,周志诚,宋克东,曹 喆
(株洲时代新材料科技股份有限公司,湖南 株 洲412007)
玻璃纤维增强PA66复合材料非等温结晶动力学的研究
陈 坤,郑梯和,周志诚,宋克东,曹 喆
(株洲时代新材料科技股份有限公司,湖南 株 洲412007)
采用差示扫描量热仪对玻璃纤维(GF)增强聚酰胺66(PA66)复合材料进行了非等温结晶研究;用莫志深法和Kissinger法计算并得到了非等温结晶动力学参数。结果表明,GF对PA66基体具有异相成核作用,可提高其结晶速率;当GF含量为30%(质量分数,下同)时,复合材料的结晶速率最大;在相同时间内,复合材料的结晶度越大,其所需的降温速率越大;PA66、PA66/15%GF、PA66/30%GF、PA66/45%GF的结晶活化能分别为-297.22、-356.32、-481.00、-365.59kJ/mol。
聚酰胺66;玻璃纤维;复合材料;非等温结晶动力学
0 前言
聚酰胺(PA)具有耐化学腐蚀性、耐磨、耐热性和自润滑等优良特性,是产量最大的工程塑料。但是由于纯PA力学性能较低,从而限制了其在各工业领域的广泛使用,因此对PA进行增强改性成为国内外研究的热点[1]。GF具有强度高、耐候、耐热、绝缘性好和价格低廉等特点而在PA的增强改性中得到广泛应用[2]。目前对PA/GF的研究主要集中在GF的含量、种类、长度和分散等因素对增强PA力学性能的影响[3-5],而对PA/GF结晶动力学的研究却报道甚少。
研究[4-5]认为结晶性是影响 PA66/GF疲劳性能的关键因素,因此研究PA66/GF结晶过程的各种参数以及了解其影响条件,可为加工成型条件优化等提供必要的科学依据[6]。因此,本研究利用差示扫描量热仪研究GF含量和冷却速率对PA66非等温结晶行为的影响,并采用莫志深法和Kissinger法对结果进处理,以期对PA66/GF复合材料的非等温结晶机理进行深入了解。
1 实验部分
1.1 主要原料
PA66,EPR27,神马实业股份有限公司;
GF,2000,兴旺玻璃纤维有限公司。
1.2 主要设备及仪器
电热恒温干燥箱,GZX-DH-3043J,上海跃进医疗器械厂;
双螺杆挤出机,FY-35,南京富亚橡塑机械制造有限公司;
差示扫描量热仪(DSC),DSC821e,瑞士梅特勒公司。
1.3 样品制备
将PA66在110℃干燥箱中干燥4h后,将其倒入挤出机机筒,挤出造粒温度为270~280℃、螺杆转速为300r/min,GF从挤出机中段加入,分别控制其含量为0、15%、30%和45%,料条经过水冷切粒。
1.4 性能测试与结构表征
DSC分析:在气体流速为50mL/min的N2保护下,以20K/min的速度从室温升到300℃,并恒温5min以消除热历史。然后分别以2.5、5、10、20K/min的降温速率冷却至室温,测定结晶过程中样品热焓值随温度的变化。
2 结果与讨论
从图1可以看出,随着降温速率的增加,同种材料的结晶放热峰位置均逐渐向低温方向移动,峰形变宽。对聚合物非等温结晶动力学的数据处理有多种处理方法,每种方法均有其使用范围和局限性。研究发现,莫志深法和Kissinger法比较适合于本体系。
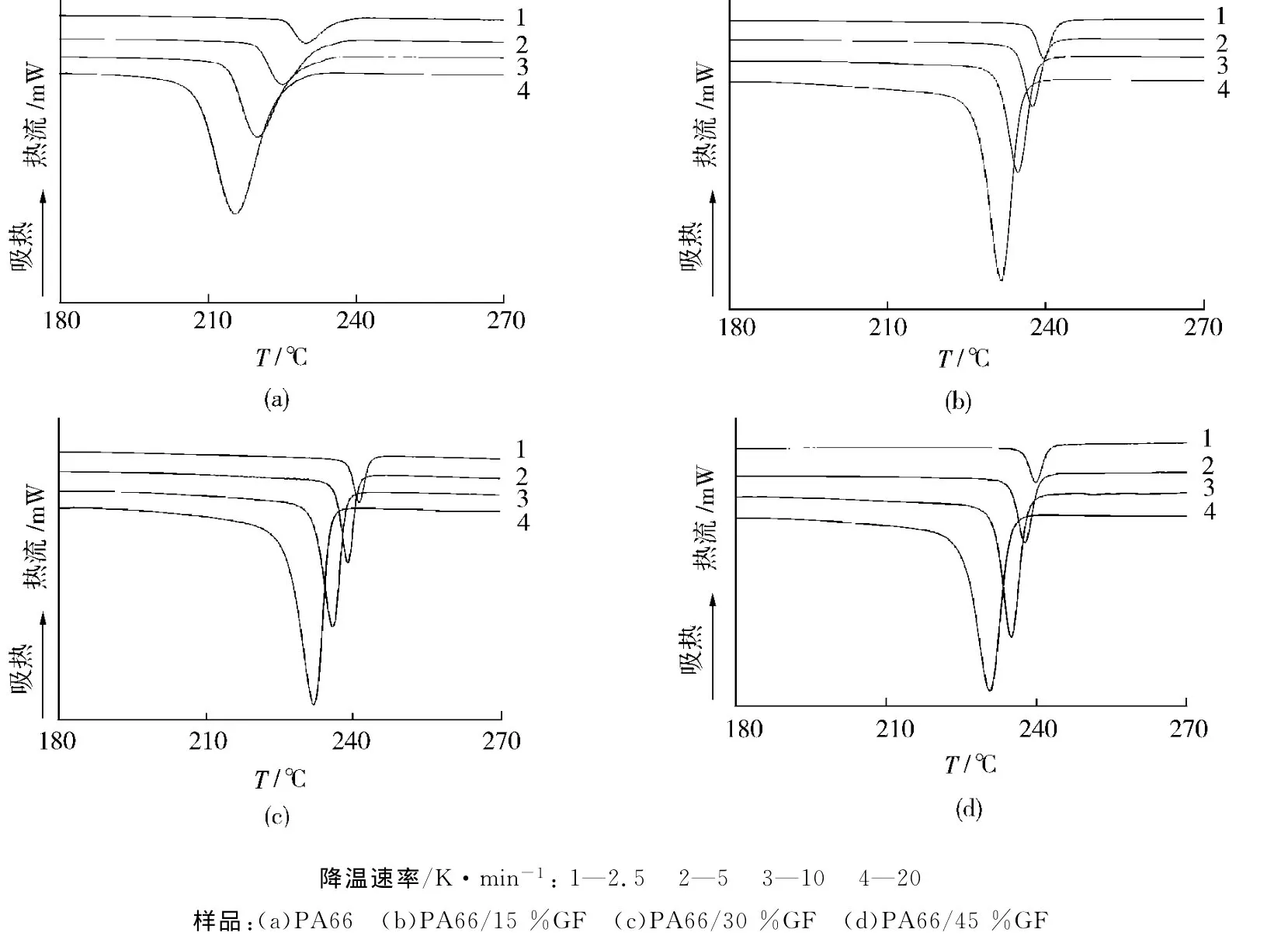
图1 PA66/GF复合材料的非等温结晶DSC曲线Fig.1 DSC curves for non-isothermal crystallization of PA66/GF composites
2.1 莫志深法非等温动力学研究
由于在不同的降温速率下,聚合物结晶的温度区间各不相同,因此应用Ozawa方程处理实验结果时,作图选点存在很大的局限性[7]。为此莫志深等综合了Avrami方程和Ozawa方程,推导了在某一给定结晶度(Xt)下的非等温结晶动力学过程,其方程式为:
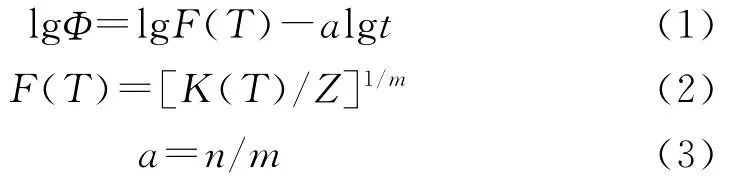
式中 Φ——降温速率,K/min
t——结晶时间,min
m——Ozawa指数
n——Avrami指数
K(T)——Ozawa法的冷却函数
Z——Avrami法的动力学常数
F(T)表示结晶速率的快慢,F(T)越大,体系的结晶速率越低。F(T)的物理意义为单位结晶时间内体系达到某一结晶度必须选取的降温速率值,表征样品在一定结晶时间内达到某一结晶度时的难易程度[8]。
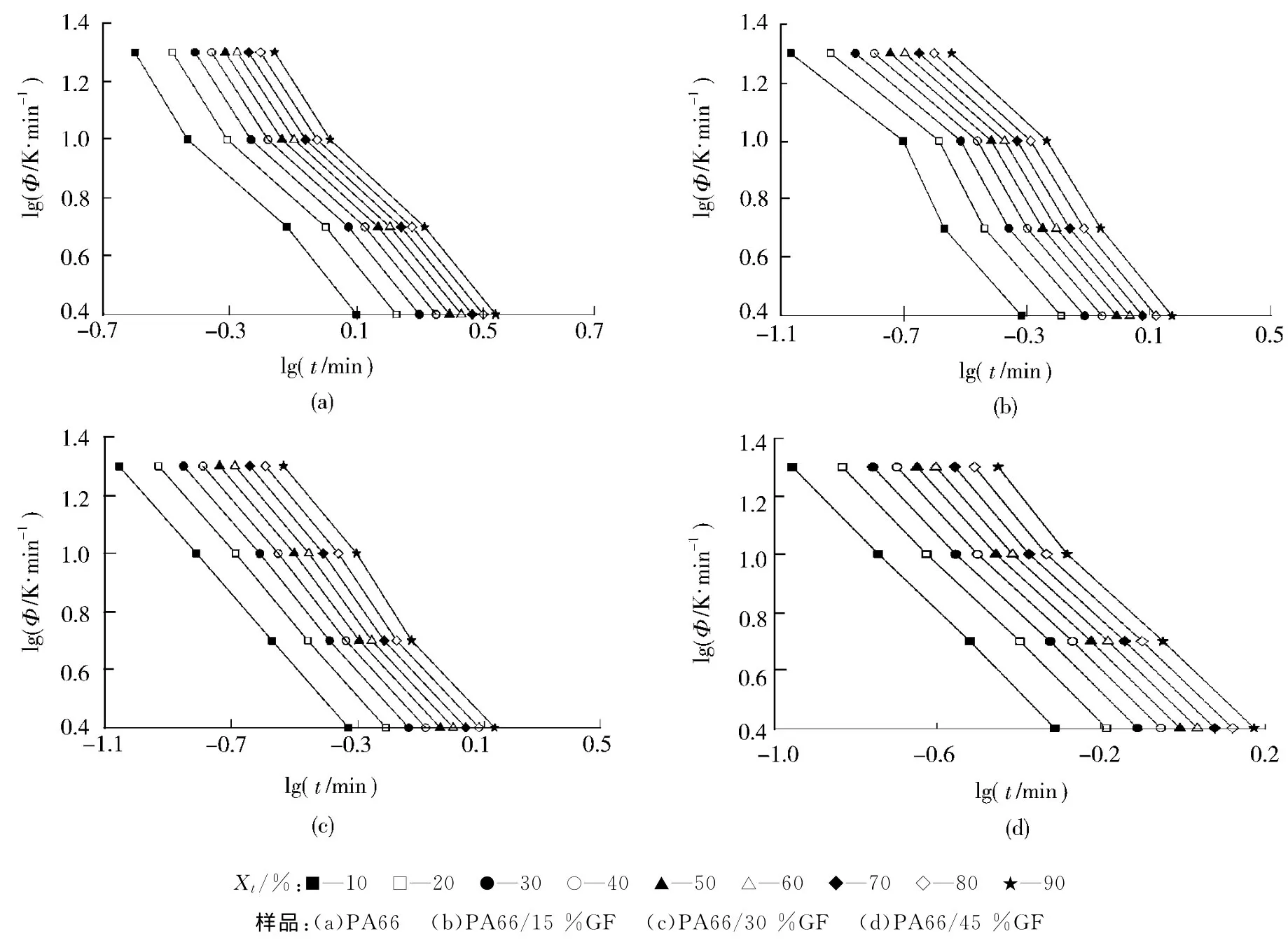
图2 lgΦ与lgt关系曲线Fig.2 Plots for lgΦversus lgt
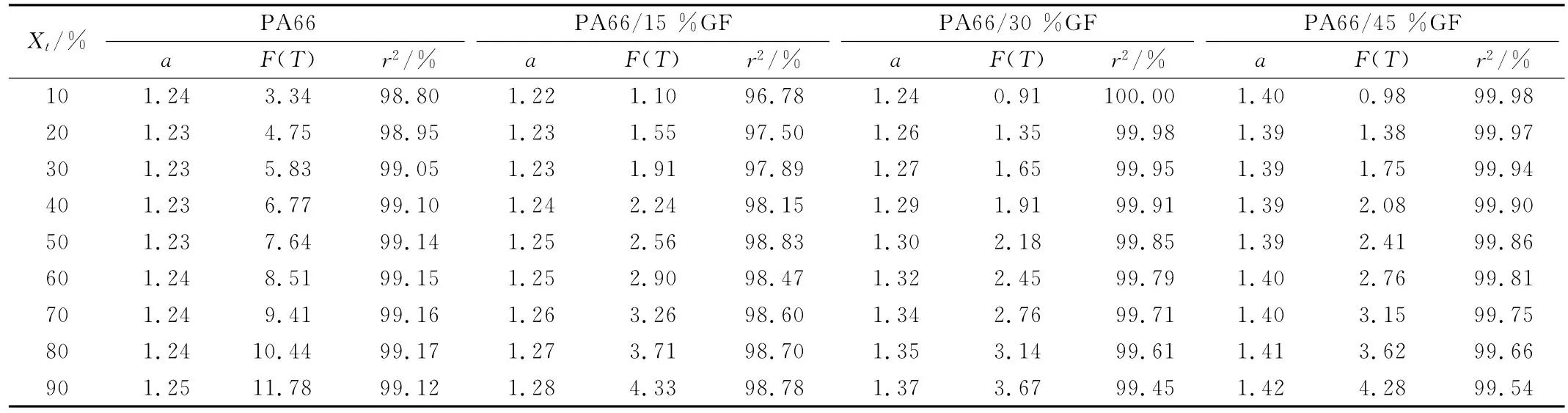
表1 采用莫志深法得到的非等温结晶动力学参数Tab.1 Kinetic parameters for the samples during non-isothermal crystallization process by Mo method
图2为lgΦ对lgt的关系图,对曲线进行拟合,由拟合曲线的斜率和截距可得到a和F(T)值,如表1所示。可以看出,各回归曲线的相关系数(r2)均在98%以上,表明线性回归效果比较理想,说明采用莫志深法对PA66及PA66/GF的非等温结晶过程进行处理是适当的。表1表明,在整个结晶过程中PA66/15%GF的a值基本一致,表明在整个结晶过程中样品的成核机理及晶体生长方式没有发生很大的变化;PA66/30%GF在结晶的过程中a随着结晶度的增大而不断增大,表明其结晶方式不断发生变化;PA66/45%GF的a均大于PA66、PA66/15%GF和PA66/30%GF,而且在整个结晶过程中,PA66/45%GF的a基本没有发生变化,这表明虽然其成核机理及晶体生长方式与PA66、PA66/15%GF和PA66/30%GF存在较大的差异,但是在整个结晶过程中其的晶体生长方式并没有发生较大的变化。此外,从表1可以看出,同一样品的F(T)值均随着结晶度的增大而增大,表明在相同的时间内,同一种材料要达到的结晶度越大,其所需的降温速率越大;在相同结晶度下,PA66/GF的F(T)均小于纯PA66的,其中PA66/30%GF的F(T)最小,说明GF加快了PA66的结晶速率,当GF含量为30%时PA66的结晶速率最快。
2.2 Kissinger测定结晶活化能
Kissinger方程可以求出结晶活化能[9]等参数,其方程为:
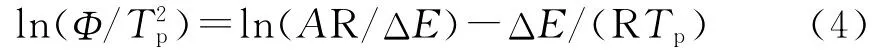
式中 A——Arrhenius方程的指前因子
ΔE——结晶活化能,kJ/mol
R——气体常数,J/(K·mol)
Tp——结晶放热峰最大值所对应的温度,K
图3为ln(Φ/T2p)对1/Tp的关系图,并对曲线进行拟合,由拟合曲线的斜率可计算得到ΔE,如表2所示。可以看出各回归曲线的相关系数r2均在95%以上,表明线性回归效果比较理想,说明采用Kissinger法计算材料的结晶活化能是适当的。表2表明,PA66/GF的结晶活化能的绝对值均大于纯PA66,这说明PA66/GF的结晶能力较强;同时从表2还可以看出,PA66/30%GF的结晶活化能的绝对值最大,说明当GF含量为30%时,复合材料的结晶能力最强,这与采用莫志深法所得到的结论一致。
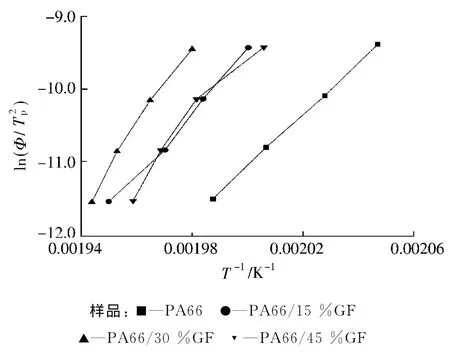
图3 ln(Φ/T2p)与1/Tp关系Fig.3 Plots for ln(Φ/T2p)versus 1/Tp
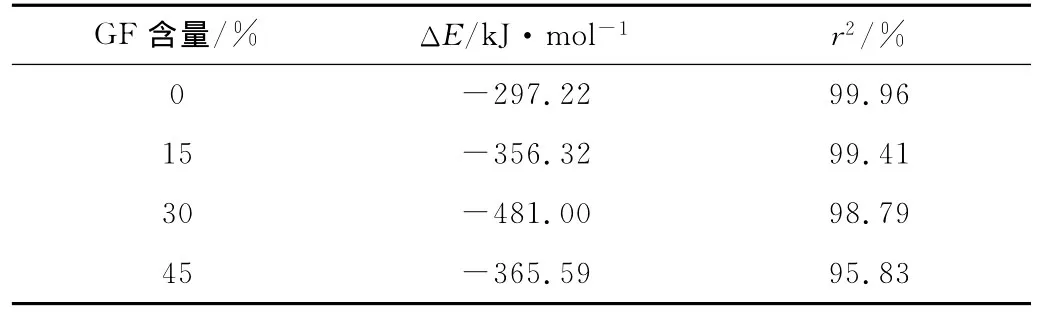
表2 样品的结晶活化能Tab.2 The crystallization activation energy of the samples
3 结论
(1)莫志深法和Kissinger法均适用于PA66/GF和纯PA66的非等温结晶过程分析,两种方法所得结论一致;
(2)GF增强了PA66的结晶能力,加快了其结晶速率,当GF含量为30%时PA66的结晶速率最大;当GF含量大于15%时,PA66的成核机理及晶体生长方式发生了较大的变化;在相同的时间内,GF增强PA66要达到的结晶度越大,其所需的降温速率越大;
(3)PA66、PA66/15%GF、PA66/30%GF、PA66/45%GF的结晶活化能分别为-297.22、-356.32、-481.00、-365.59kJ/mol。
[1] 刘相果,彭晓东,刘 江,等.偶联剂对短玻纤增强PA66微观结构及性能影响研究[J].工程塑料应用,2003,31(7):1-4.
Liu Xiangguo,Peng Xiaodong,Liu Jiang,et al.Study on the Influence of the Coupling Agent on the Microstructure and Mechanical Properties of Short Glass Fiber Reinforced PA66[J].Engineering Plastics Application,2003,31(7):1-4.
[2] 邓如生.共混改性工程塑料[M].北京:化学工业出版社,2003:166-167.
[3] 王 艇.玻璃纤维增强聚酰胺性能的研究[J].化工技术与开发,2010,39(2):18-21.
Wang Ting.Performance Study of Glass Fiber Reinforced Polyamide[J].Technology & Development of Chemical Industry,2010,39(2):18-21.
[4] 刘亚庆.玻纤增强尼龙66疲劳性能的研究[J].工程塑料应用,2002,30(8),43-44.
Liu Yaqing.Study on the Fatigue Property of Glass Fiber Reinforced PA66[J].Engineering Plastics Application,2002,30(8),43-44.
[5] 谭亮红,欧阳振中,周淑华,等.玻纤增强尼龙66产品性能差异原因分析[J].现代塑料加工应用,2004,16(2):33-34.
Tan Lianghong,Ouyang Zhenzhong,Zhou Shuhua,et al.Analysis of the Properties Difference Between Products Made from Glass Fiber Reinforced Nylon66[J].Modern Plastics Processing and Applications,2004,16(2):33-34.
[6] 梁淑君,杨万泰.PAG原位增容PP/PA6共混物的非等温结晶动力学[J].中国塑料,2010,24(3):34-40.
Liang Shujun,Yang Wantai.Non-isothermal Crystallization Kinetics of Polypropylene/Polyamide 6Blends Insitu Compatibilized with PAG[J].China Plastics,2010,24(3):34-40.
[7] 刘结平,莫志深.聚合物结晶动力学[J].高分子通报,1991,(4):199-207.
Liu Jieping,Mo Zhishen.Crystallization Kinetics of Polymers[J].Chinese Polymer Bulletin,1991,(4):199-207.
[8] 殷敬华,莫志深.现代高分子物理学(上册)[M].北京:科学出版社,2001:111-112.
[9] 胡荣祖,高胜利,赵凤起,等.热分析动力学[M].北京:科学出版社,2008:79-80.
Study on Nonisothermal Crystallization Kinetics of Glass Fiber Reinforced PA66Composites
CHEN Kun,ZHENG Tihe,ZHOU Zhicheng,SONG Kedong,CAO Zhe
(Zhuzhou Times New Material Technology Co,Ltd,Zhuzhou 412007,China)
The crystallization behavior of glass fiber reinforced PA66composites was characterized using DSC.Parameters of isothermal and non-isothermal crystallization kinetics were calculated using of Mo and Kissinger methods.It showed that glass fiber played as a heterogeneous nucleating agent,which increased the crystallization rate of PA66.When the glass fiber content was 30%,the crystallization rate reached the maximum.The greater the cooling rate,the greater the degree of crystallinity.The crystallization activation energy of the composites were-297.22,-356.32,-481.00,and -365.59kJ/mol,respectively,when the glass fiber contents were 0,15%,30%,and 45%.
polyamide 66;glass fiber;composite;nonisothermal crystallization kinetics
TQ323.6
B
1001-9278(2012)08-0031-04
2012-03-18
联系人,76206690@163.com

