电动注塑机用滚珠丝杠副的动态应力分析
沈雪明,袁卫明,陈法鑫,刘际轩,李凌丰
(1.浙江申达机器制造股份有限公司,浙江杭州310038;2.浙江大学机械工程学系,浙江杭州310027)
电动注塑机用滚珠丝杠副的动态应力分析
沈雪明1,袁卫明1,陈法鑫1,刘际轩2,李凌丰2
(1.浙江申达机器制造股份有限公司,浙江杭州310038;2.浙江大学机械工程学系,浙江杭州310027)
通过建立电动注塑机用滚珠丝杠副接触角等结构参数以及速度和加速度的动态受力模型,利用螺母和丝杠的速度关系,得到二者之间加速度的关系。应用赫兹应力公式推导出螺母侧和丝杠侧的接触应力公式,并进一步分析了接触角等结构参数以及速度和加速度对丝杠副接触应力的影响。结果表明,对于电动注塑机用滚珠丝杠副,速度的增大会造成接触应力的明显增加,加速度的增加也会造成接触应力的增加。
滚珠丝杠副;电动注塑机;动态受力模型;加速度;离心力;赫兹接触应力
0 前言
全电动注塑机具有环保、节能、噪声低、注射控制精度高、制品品质好等优点,但在合模动作时,其合模机构中滚珠丝杠副由于负载大而磨损较为严重。对于这一问题,目前还没有很好的解决办法[1-2]。滚珠螺旋丝杠副实际工作过程中内部及外部复杂的传动力学因素往往是造成滚珠丝杠副失效的主要原因。失效是由接触应力引起的接触疲劳破坏造成的,降低滚珠接触应力可有效抑制滚珠、丝杠及螺母的磨损,从而提高滚珠丝杠副的工作寿命。国内外许多学者对滚珠丝杠副的弹性变形和接触应力进行了深入研究。程光仁等[3]对滚珠丝杠副的接触变形进行了原理性阐述;Wei等[4]对考虑弹性变形和变化的接触角情况下的滚珠丝杠副进行了动态分析;Mei等[5]对存在加工误差情况下滚珠间的载荷分布进行了计算,提出可通过正向误差来使载荷分布更加均匀,但误差会引起滚珠丝杠副的振动;Braccesi等[6]应用弹塑性理论对返回装置变形前后的载荷及应力进行了计算和分析。但这些研究都集中于研究工艺参数对接触应力的影响,运动参数方面的研究还很少,而合模用丝杠副在实际工作过程中是变速运动,工作负荷也随着工作过程不断变化,滚珠和螺母都受到一定程度的冲击,另外,当丝杠高速运转时,滚珠离心力的作用也不可忽略。
本文主要通过建立滚珠丝杠副的动态受力模型,将丝杠侧和螺母侧区别开来,分别推导出包含接触角等结构参数以及速度和加速度的弹性形变公式,并进一步分析丝杠副的结构参数以及转速和加速度对接触应力的影响。为方便计算:本文作以下假设:(1)忽略摩擦力和润滑因素;(2)滚珠与丝杠和螺母之间是纯滚动。
1 滚珠丝杠副动态受力模型
建立如图1所示坐标系,X′OYZ′和XOYZ坐标系,X′轴是丝杠轴线方向,YOZ′为丝杠轨道法向截面。
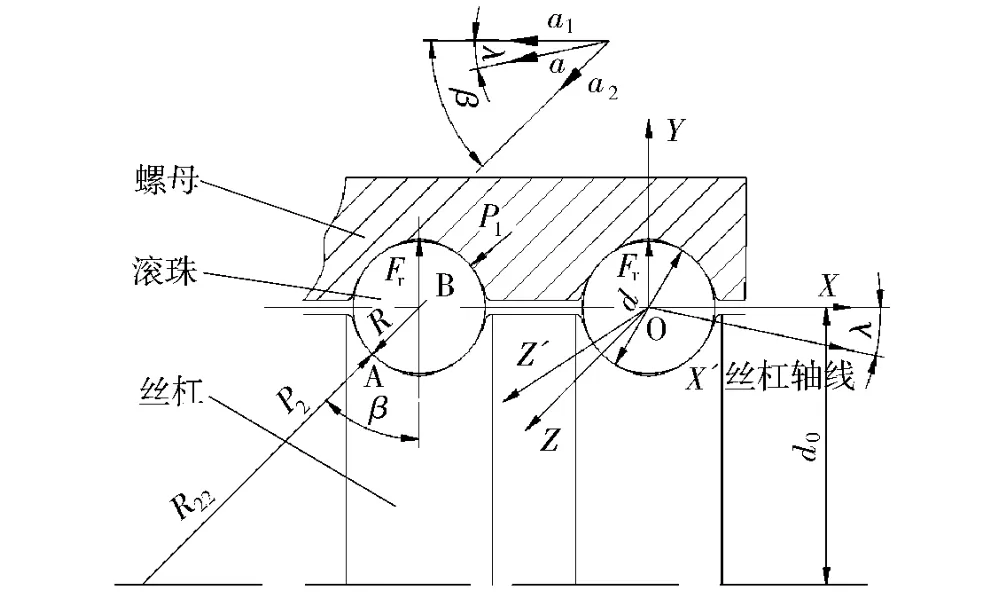
图1 丝杠副动态受力模型Fig.1 Dynamic stress model of ball screw
设滚珠直径为d,滚珠螺旋副的滚珠中心圆直径为d0,t为滚道曲率比值,是一设计经验值,接触角为β,螺旋升角为λ,导程为L,滚珠丝杠副工作时的瞬时载荷为F,丝杠转速为n,螺母直线运动速度为v,加速度为a,滚珠水平方向的加速度为a1,在接触力方向上的加速度为a2。滚珠在A点和丝杠接触,在B点和螺母接触,考虑到加速度的存在和曲率半径的不同,2点的接触应力显然不同。
不考虑滑动,滚珠中心的线速度(v0)为[7]:

丝杠旋转一周,螺母前进一个导程,可以得到螺母的速度:

分别对公式(1)和(2)求导,可得加速度之间的关系:
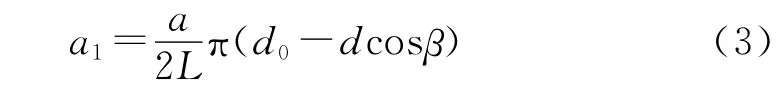
由图1几何关系可知:
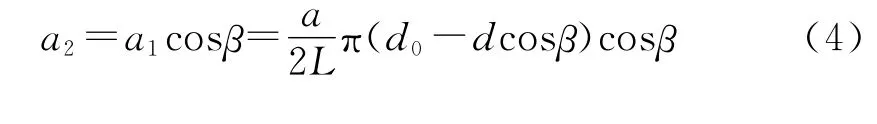
2 滚珠与丝杠和螺母接触点的主曲率
如图1所示,滚珠与螺母轨道接触点B处的4个主曲率分别为:

式中 R——螺母滚道的一个曲率半径
螺母侧综合曲率为:

滚珠与丝杠轨道接触点A处的4个主曲率分别为:
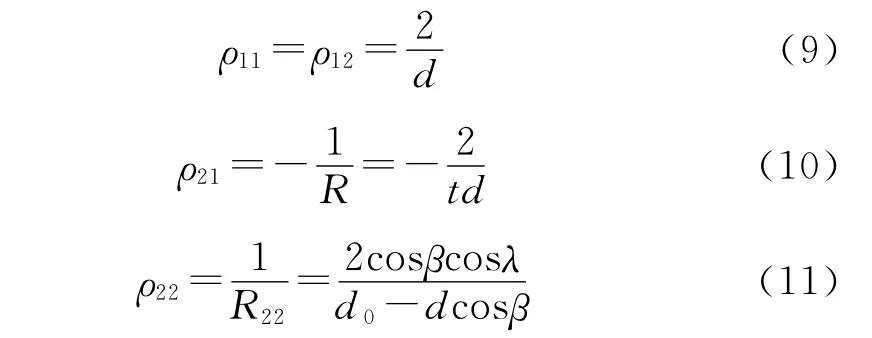
式中 R22——丝杠滚道的一个曲率半径
丝杠侧综合曲率为:

3 动态载荷与结构、运动参数的关系
考虑到螺母加速度的影响,实际工作的载荷(Fd)为:
式中 m1——工作台质量
考虑螺旋升角的影响,若认为在理想工作情况下,轴向工作载荷均匀地分配给所有的工作滚珠,且每个滚珠的法向力的合力通过丝杠轴线,忽略摩擦力因素,则法向力(P)为:

式中 z——总的工作滚珠数,可以用式(15)近似求
取:

式中 i——滚珠螺母的工作圈数乘以列数
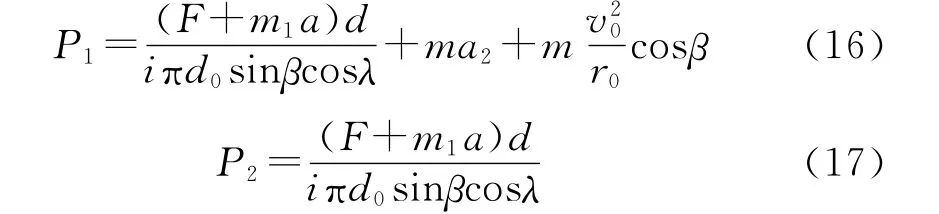
式中 m——滚珠质量
a2——接触力方向上的加速度
r0——滚珠螺旋副的滚珠中心圆半径
P1——螺母表面法向力
P2——丝杠表面法向力
4 动态弹性接触变形计算
根据弹性接触理论,2个自由弹性体在压力P作用下点接触时,接触椭圆区各点的应力按半椭球规律分布,其值为[8]:
矿床储量规模分布的数学模型是根据矿床储量的统计自相似性,应用概率统计方法建立模型,并通过模型及其分维值的数理分析,得出不同分维值的地学解释 [3] 。
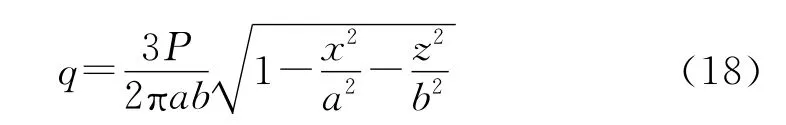
其中,长半轴(a)、短半轴(b)的计算公式为:

式中 α、γ——主曲率确定的几何系数,由文献[9]确定
μ1、μ2——材料的泊松比
E1、E2——材料的弹性模量
进一步求出最大接触应力为:

Z轴方向上,丝杠侧和螺母侧曲面均被压缩,压缩量为:

式中 J——主曲率值决定的椭圆积分
当2个弹性体均为钢时,由于钢的弹性模量E=2.1×105MPa,泊松比μ=0.3,螺母表面的接触弹性形变为:

同理可得丝杠表面的接触弹性形变:

由式(25)和(26)可知,滚珠丝杠副的结构参数以及运动参数对于丝杠和丝杠螺母的接触应力起着决定性的作用。
5 算例和动态接触应力影响因素分析
以某型号电动注塑机上滚珠丝杠副为例,分析相关的结构参数、速度和加速度对丝杠副接触应力的影响。滚珠丝杠副工艺参数如表1所示。

表1 滚珠丝杠副的结构参数Tab.1 Structural parameters for ball screw
由于滚珠丝杠副整个工作过程中仅注塑过程存在较大的力的变化,而整个注塑过程可分为图2中的5个步骤,根据工作压力曲线图2所示,用5段压力近似代替整个注塑过程,确定各段压力所占时间比例。由于纵向力与压力成线性关系,相应地计算各段的工作压力值,将计算数值列于表2。滚珠丝杠副的运动参数如表3所示。
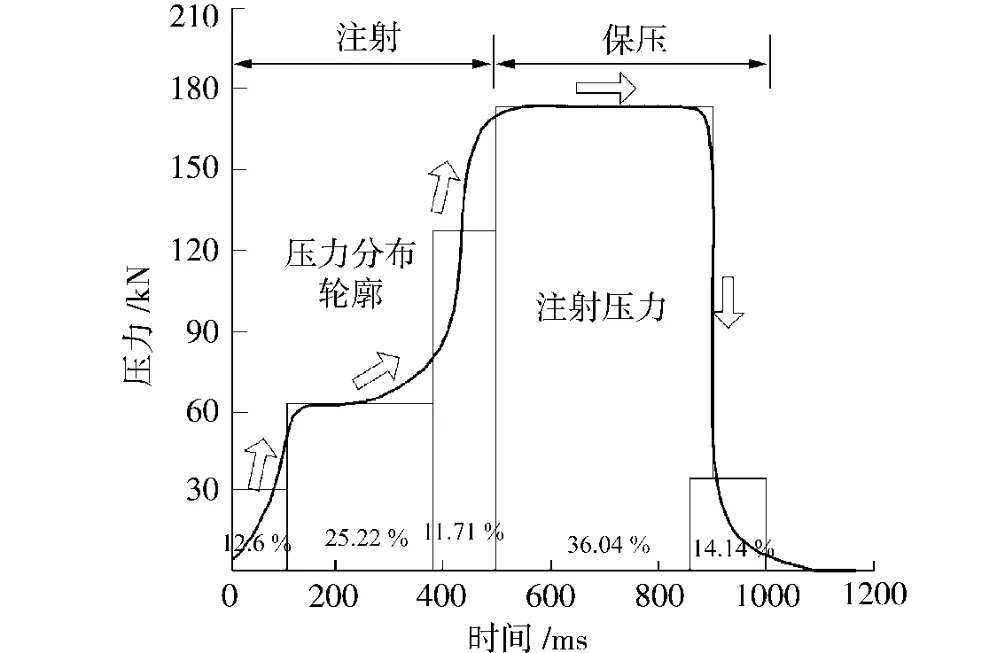
图2 注塑过程的压力曲线Fig.2 Pressure curve for plastic injection process

表2 注塑过程的压力值Tab.2 Pressure value for plastic injection process

表3 滚珠丝杠副的运动参数Tab.3 Motion parameters for ball screw
5.1 接触角β对动态接触应力的影响
根据公式(18)和(19)得到图3的弹性变形和接触角的关系。由图3可知,随着接触角的不断增大,螺母侧和丝杠侧接触应力都是不断减小,当接触角β接近45°(β=0.7854rad),接触弹性变形量趋于平缓。因此,合理地增大接触角,不仅仅可以减少接触应力,还可以适当地提高定位精度。但当接触角>45°时,接触应力的变化就不再明显,而且接触角的增大会增加螺旋轨道的加工难度,因此设计时β通常不大于45°。另外,丝杠侧和螺母侧的弹性变形之所以出现图3中的差异,除了综合曲率半径不同之外,滚珠产生的离心力大大增加了螺母侧的弹性形变。
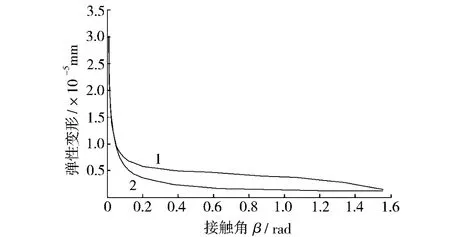
图3 接触应力和接触角β之间的关系Fig.3 Relationship between contact stress and contact angleβ
5.2 螺旋升角λ对动态接触应力的影响
根据(25)和(26)得到图4中弹性变形量和螺旋升角的关系。由图4可知,丝杠侧弹性变形量变化趋势和螺母侧一致,随着螺旋升角的增大,接触应力不断增大,丝杠侧的接触应力之所以小于螺母侧是因为螺母侧要承受来自滚珠的离心力的作用。但考虑到螺旋角与导程之间存在所以螺旋角越小,导程越小,滚珠丝杠副的传动效率就会急剧降低,高速化性能也会减弱。再考虑到大导程丝杠副的加工是一个难题,所以一般螺旋升角的取值在3°~10°。
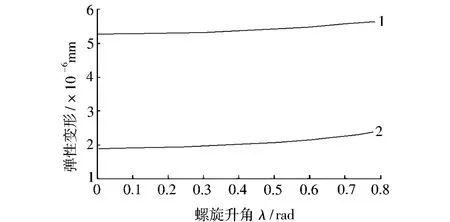
图4 接触应力和螺旋升角λ的关系Fig.4 Relationship between contact stress and lead angleλ
5.3 速度对动态接触应力的影响
滚珠在螺旋轨道内运动时,会产生离心力的作用,如图5所示,随着速度的不断增大,螺母侧的弹性变形量逐渐变大,速度提高10%,接触弹性变形量也提高10%,基本呈现线性变化趋势,丝杠侧不发生变化。所以对于高速重载的滚珠丝杠副,滚珠质量大,运转速度高,此部分的作用力十分明显。因此,实现重载滚珠丝杠副高速化是很困难的。

图5 接触应力和速度的关系Fig.5 Relationship between contact stress and speed
5.4 加速度对动态接触应力的影响
实际工作过程中,合模机构不是匀速运动,螺母也就不可能匀速运动,滚珠也不可能匀速地运行,故工作台和滚珠速度地变化都会造成冲击载荷,从而使接触应力增大。本文讨论的是高速重载滚珠丝杠副,加速度基本维持在5~15m/s2。如图6所示,在加速度影响下,螺母侧和丝杠侧的弹性形变趋势基本一致,加速度增加1m/s2,弹性变形量增加0.5μm。相对离心力引起的变化,加速度对接触应力的影响较小。但对于冲击载荷较大的滚珠丝杠副,加速度达到一定值时对丝杠副的破坏还是十分明显的。

图6 接触应力和加速度的关系Fig.6 Relationship between contact stress and acceleration
5.5 滚珠螺旋副的滚珠中心圆直径d0对动态接触应力的影响
由式(16)和(17)知,滚珠与螺旋轨道的接触应力与滚珠螺旋副的滚珠中心圆d0成反比,d0的增加也会明显增加丝杠的抗扭刚度和强度,而且,d0增加使设计大直径滚珠的滚珠丝杠副成为可能,滚珠直径越大,承受载荷的能力越强,这对高速重载的滚珠丝杠副具有很大的意义。但美中不足的是d0增加会造成丝杠副的尺寸增加,而滚珠直径的增大会造成离心力的增加。
6 结论
(1)滚珠丝杠副的结构参数决定了其工作性能,接触角增大有利于减少接触应力;螺旋升角增大不仅增加接触应力,而且会使加工更加困难;滚珠螺旋副的滚珠中心圆d0和丝杠副接触应力近似反比例变化;
(2)速度对丝杠侧的接触应力影响不大,但对螺母侧接触应力造成很大影响,速度越大,接触应力越大,加速度对丝杠侧和螺母侧都会产生影响,加速度越大,接触应力也越大;
(3)本文推导出的公式,不仅适用于注塑机用滚珠丝杠副,对于普通的滚珠丝杠副也适用。
[1] 黄步明,许忠斌.高超密精密注塑机的技术进展及发展动向[J].工程塑料应用,2002,30(12):47-49.
Huang Buming,Xu Zhongbin.Technology Development Trend of Carmel High Precision Injection Molding Ma-chine[J].Engineering Plastics Application,2002,30(12):47-49.
[2] Maruyama D,Miyaguchi K.Development of HTF Series Ball Screws for High Load Drive Application[J].Motion&Control,2002,13:27-34.
[3] 程光仁,施祖康,张超鹏.滚珠螺旋传动设计基础[M].北京:机械工业出版社,1987:72-102.
[4] Wei Chin Chung,Lin Jen Fin.Kinematic Analysis of the Ball Screw Mechanism Considering Variable Contact Angles and Elastic Deformations[J].Journal of Mechanical Design,2003,125:717-733.
[5] Mei Xuesong,Tsutsumi M,Tao T,et al.Study on the Load Distribution of Ball Screws with Errors[J].Mechanism and Machine Theory,2003,38:1257-1269.
[6] Braccesi C,Landi L.A General Elastic-plastic Approach to Impact Analysis for Stress State Limit Evaluation in Ball Screw Bearings Return System[J].International Journal of Impact Engineering,2007,34:1272-1285.
[7] 姜洪奎.大导程滚珠丝杠副动力学性能及加工方法研究[D].济南:山东大学机械工程学院,2007.
[8] 徐芝纶.弹性力学(上册)[M].北京:高等教育出版社,2006:295-302.
[9] Liukexin B C.刀具设计的螺旋面理论[M].北京:机械工业出版社,1984:9-10.
Dynamic Stress Analysis of Ball Screw for Electric Operated Injection Molding Machine
SHEN Xueming1,YUAN Weiming1,CHEN Faxin1,LIU Jixuan2,LI Lingfeng2
(1.Zhejiang Sound Machinery Manufacture Co,Ltd,Hangzhou 310038,China;2.Department of Mechanical Engineering,Zhejiang University,Hangzhou 310027,China)
A dynamic force model of the ball screw used for electric operated injection molding machine was established using contact angle,velocity,acceleration,and others as structure parameters.Relationship between the velocity and acceleration of nut and screw was obtained.The contact stress at the nut and screw sides was described in terms of Hertz stress formula,and the effect of the structure and motion parameters on the contact stress of ball screw was further analyzed.It showed that,for a ball screw,increase in either velocity or acceleration could cause increase in contact stress significantly.
ball screw;injection molding machine;dynamic force model;acceleration;centrifugal force;Hertz contact stress
TQ320.66+2
B
1001-9278(2012)03-0103-05
2011-12-30
联系人,zjsounddjs@163.com
(本文编辑:刘 学)

