奇性函数的加权Stancu算子逼近
高珊珊,赵 易,于 蛟
(杭州电子科技大学数学研究所,浙江杭州310018)
0 引言
算子逼近是逼近论中的重要部分,而最重要的类型之一就是Bernstein算子对函数的逼近。之前关于该算子的研究已相对充分,在理论中得到了许多结论,并应用于神经网络、数据拟合等相关问题。本文考虑的是Bernstein算子的更一般推广—Stancu算子,研究该算子对于端点处具有奇性函数的逼近,利用光滑模、K-泛函等逼近工具,给出相应的估计。本文考虑了Stancu算子对在端点处具有奇性的函数的加权逼近,并通过Ditzian-Totik光滑模ω2φ(f,δ)对该算子的逼近阶作出具体估计。
1 相关定义
(1-x)β,α,β≥0,α+β〉0,0≤x≤1,记 Cw= {f(x)∈C(0,1):lxim1(wf)(x)=lxim0(wf)(x)=0},范数
→→‖wf‖w=sup(wf)(x)。记= {f∈Cw:f'∈AC[0,1],‖wφ2f″‖〈∞ },其中φ(x)=二阶光滑模定义,且K-泛函定义:,δ2):={‖w(f-g)‖ +δ2‖wφλg″‖ },显然(见文献4Ditzian,Z.,Totic,V.)
本文构造了一类新的Stancu算子逼近上述函数,此时需将Stancu算子修正为:
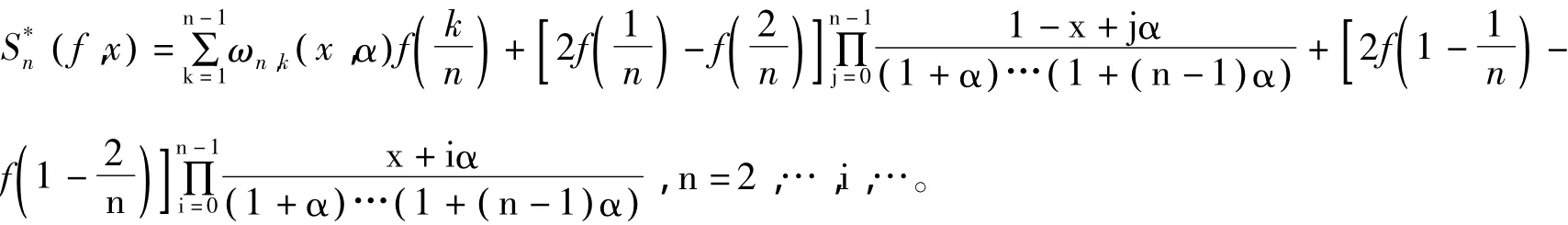
2 主要结果
定理3 对 f∈Cw,且α=α(n)=O(n-1),则
3 相关引理及证明
引理1 对于 ωn,k(x)=1((1-x)(n-k,-α),有
引理 2 对 于 ωn,k(x)=,对于任意的 u,v≥0,则有
4 定理的证明
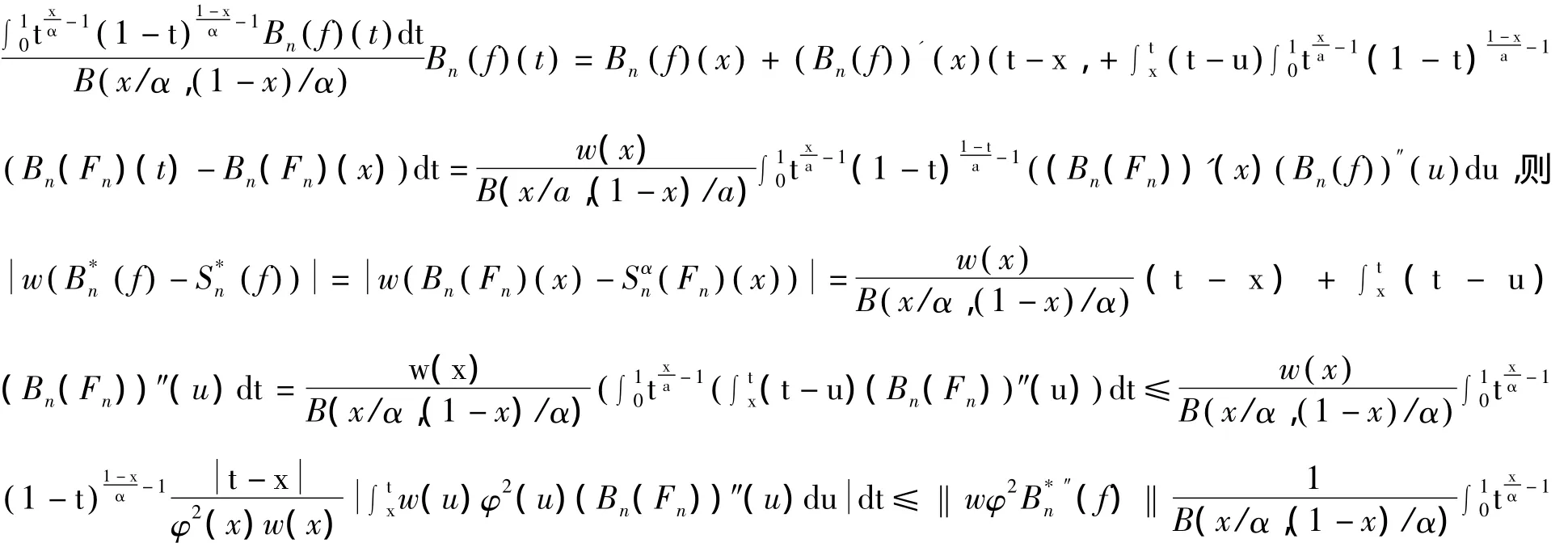
5 结束语
本文在全局逼近和点态逼近的基础上将Bernstein算子的一些性质平行推广到Stancu算子上,得到了相应结论,并且给出了相应的逼近阶。
[1] 王丽,薛银川.Stancu算子与连续模[J].宁夏大学学报(自然科学版),2001,22(4):360-361.
[2] 刘生贵,薛银川.一族Stancu型算子的逼近[J].宁夏大学学报(自然科学版),2006,32(3):486-491.
[3] Della Vecchia,Mastroianni B ,Szabodos G.Weighted approximation of functions with endpoint or inner singularities by Bernstein operators[J].Acta MathHungar J,2004,2(12):223-239.
[4] Ditzian Z,Totik V.Moduli of Soothness[M].New York:Springer-Verlag,1987:36-43.
[5] Stancu D D.Approximation of function by a new class of linear polynomial operators[J].Rev Roumaine Math Pure App1,1968,13(1):488-490.
[6] Wei Bao-rong,Zhao Yi.Weighted approximation of functions with singularities by Bernstein operators[J] .Journal of Zhejiang University science A,2008,9(10):1 451-1 456.

