一类具有尺度分布的捕食系统模型的定性分析
王启民,何泽荣,江晓东
(杭州电子科技大学理学院运筹与控制研究所,浙江杭州310018)
0 引言
种群是生态学研究的重要单元,国内外学者进行了大量研究,积累了丰富的成果。就尺度分布模型而言,连续模型较多[1-3],离散模型较少[4]。自从提出种群的离散模型并详细分析了种群的稳定分布后,一些研究者尝试从离散角度来研究种群的动力学行为[4]。本文应用差分逼近法研究模型非负解的存在性问题,为其应用打好基础。
1 模型
本文提出下列模型:
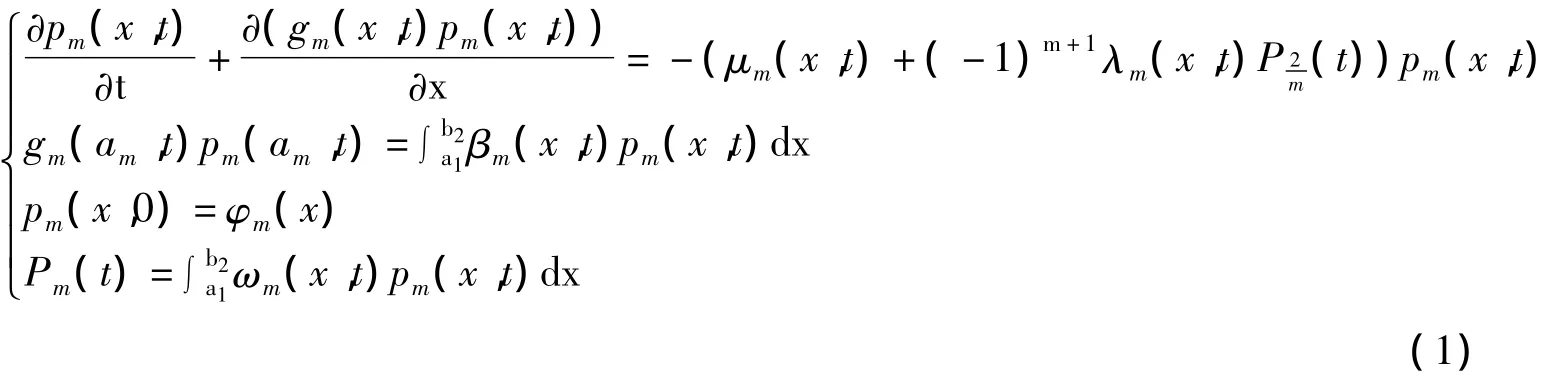
式中,a1〈x 〈b2,0 〈t〈T,m=1,2,pm(x,t),gm(x,t),βm(x,t),μm(x,t),λm(x,t),ωm(x,t),φm(x),Pm(t)分别表示食饵和捕食者种群个体尺度密度,增长率,繁殖率,死亡率,相互作用因子,权重函数,初始密度,加权总量。
2 先验估计
引理1 如果 ωm(x,t),m=1,2,在 Q 上有界,则 Pm(t)在[0,T]上有界。
3 解的存在性
本节应用差分逼近法证明式1解的存在性。对于 m=1,2给出下列基本假设:(1)βm(x,t),μm(x,t),λm(x,t),ωm(x,t)是关于 x,t的非负连续可微函数,(x,t)∈Q,并且为常数,满足2g b×[μm(x,t)-λm(x,t)Pm(t)]≥0;()m(x,t)是关于 x,t的连续可微函数,gm(x,t)〉0,x∈[a,)[0 ,T],gm(b,t)=0;(3) 对于充分小δ 〉0〈 + ∞;(4)φm(x)∈BV[a,b],φm(x)≥0,满足 gm(am,0)φm(am)=
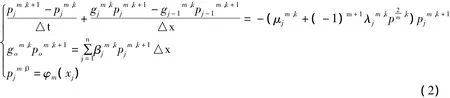
式中,j=0,1,2,…,n,k=0,1,2,…,L-1,m=1,2,pm,k△x,定义)T,则式 1 可等价写成下面的系统方程:

可以看出式3存在唯一一组非负解。
引理2 假设 Δt满足 w1mΔt〈1,对于 m=1,2,有‖‖1≤ (1 -Δ t)-k‖pm,0‖1。
证明 在式2的第一个方程两端分别乘以Δx,对j=1,2,…,n求和得到:因此
定理1 由引理6所定义的极限函数p1(x,t),p2(x,t)是式1的解。
证明 令φ(x,t)∈ C1(Q),记φ (xj,tk)。则有Δt。取极限 n→∞,L→∞知 pm(x,t)满足解的定义。
4 结束语
本文在提出一类具有尺度分布的食饵-捕食者种群系统模型的基础上,首先证明了模型解的有界性,然后对模型进行离散化,应用差分逼近方法及文献5相关结论进一步研究了模型非负解的存在性。
[1] JamesWSinko,William Streifer.A New Model For Age-Size Structure of A Population[J].Journal of Ecology ,1967,48(6):910-918.
[2] Oldfield D G.A Continuity Equation For Cell Population[J].Bulletin of Mathematical Biophysics,1966,28(1):545-553.
[3] Farkas JZ.Stability Conditions For A Non-Linear Size-Structured Model[J].Nonlinear Analysis:Real World Applications,2005,6(5):962-969.
[4] Leslie P H.On the use of matrices in certain population mathematics[J].Journal of Biometrika,1945,33(3):183-212.
[5] Smoller J.Shock Waves And Rection-Diffusion Equations[M].New York:Springer-Verlag,1994:276.

