模糊Petri网的合成运算
薛 瑜,李承家
(杭州电子科技大学理学院,浙江杭州310018)
0 引言
合成技术在Petri网中的应用成为很多学者的研究课题,为复杂大系统的建模分析提供了一个有效途径[1,2]。模糊Petri网[3]是模糊集理论和Petri网结合起来形成的新模型。由于模糊Petri网对知识表示和推理的独特优点,近年来,很多学者对其进行研究,主要集中在模糊产生式系统的FPN形式化推理算法研究及算法改进方面[4-6]。然而关于模糊Petri网的行为理论分析这方面的文献很少。模糊Petri网是Petri网的一个重要方向,因而Petri网的合成技术对模糊Petri网的合成技术研究有一定的借鉴作用。目前,不同文献提出许多不同形式的模糊Petri网的定义。本文主要介绍文献7提出的模糊Petri网的概念,然后给出了模糊Petri网的合成运算的定义,并以关联矩阵为工具讨论了合成网与原子网的关系。
1 模糊Petri网
1.1 模糊Petri网的定义
定义1 模糊 Petri网是一个六元组,记 Σ ={P,T,F,M0,W,D},其中:
(1)P={p1,p2,…,pn}为非空库所集,T={t1,t2,…,tm}为非空变迁集,P∩T= φ,库所一般用圆圈表示,变迁用短线表示;
(2)F⊆(P×T)∪(T×P);
(3)M0:P→[0,1]表示初始标识,Mi0表示库所pi的真值度;
(4)W:F→(0,1]称为权函数;w(p,t)表示前提条件p对规则成立的支持度,w(t,p)表示变迁t的发生对结果的影响程度;
(5)D:T→(0,1]表示变迁t对各个前提条件的支持度的最低要求,即变迁的阈值。
定义 2 设 N=(P,T;F)为一个网。∀x∈P∪T,记x= {y|(y∈P∪T)∧ ((y,x)∈F)},x˙={y|(y∈P∪T)∧ ((x,y)∈F)},则称x和x˙分别为x的前集和后集。
1.2 模糊Petri网的运行规则
(1)对 t∈T,如果∀p∈·t都有 M(p)·w(p,t)≥D(t),则变迁 t可以发生,记为 M[t〉。
(2)变迁t的发生产生新的标识M',记为M[t〉M',记F(a)=,则

2 合成运算
对于复杂的网系统,虽然通过化简技术可以简单便捷的研究分析,但是系统结构稍加变化,化简工作就需重新进行,在一定程度上带来不便。因而Petri网的合成运算成为很多学者的研究课题。许多文献中讨论的合成运算都是针对原型Petri网研究的。为了研究结构复杂的模糊Petri网系统,这里把合成运算的概念引申到模糊Petri网。
2.1 定义
定义 3(共享合成)设有两个模糊 Petri网 Σ1和 Σ2,Σi={Pi,Ti,Fi,Mi0,Wi,Di}(i=1,2)满足P1∩P2≠φ,T1∩T2= φ。令 Σ ={P,T,F,M0,W,D}其中 P=P1∪P2,T=T2∪T2,F=F1∪F2,且∀t∈T1,则称Σ是Σ1和Σ2的共享合成网,记作Σ=Σ1CPΣ2。
定义 4(同步合成)设有两个模糊 Petri网 Σ1和 Σ2,Σi={Pi,Ti,Fi,Mi0,Wi,Di}(i=1,2)满足P1∩P2= φ,T1∩T2≠φ。令 Σ ={P,T,F,M0,W,D}其中 P=P1∪P2,T=T2∪T2, F=F1∪F2,且∀t∈T1,则称Σ是Σ1和Σ2的同步合成网,记作Σ=Σ1CTΣ2。
合成模糊Petri网的运行规则与定义1的模糊Petri网的一样。
2.2 合成模糊Petri网与原子网的关系
Petri网有多种分析方法,其中代数分析方法主要以关联矩阵的形式对一个网系统的结构给予刻画,然后建立状态可达的线性系统关系。这种方法可以简洁的展示Petri网的一些结构性质。文献7利用关联矩阵提出有效形式化算法和图形与形式化推理相结合的混合算法讨论模糊Petri网的运行规律,使网的运行简洁化,可视化。由于模糊Petri网在行为理论上分析工具很少,因此本文从关联矩阵的角度讨论合成网与原子网的关系。
为讨论方便,用Ai*表示矩阵A的第i行形成的行向量,用A*j表示矩阵A的第j列形成的列向量。矩阵A ~i-是矩阵A删除第i行行向量得到的矩阵,矩阵A~-j是矩阵A删除第j列列向量得到的。
给出两个模糊 Petri网 Σi(i=1,2),令|P1|=n1,|T1|=m1,|P2|=n2,|T2|=m2。网 Σi的输入矩阵为I(i),输出矩阵为O(i)(i=1,2);分别记作:

由子网的关联矩阵A1和A2可以得出合成网的关联矩阵A。
设模糊Petri网Σ由模糊Petri网Σ1和Σ2共享合成的。假设pi即为公共库所。则合成网Σ的输入输出矩阵分别为I=
设模糊Petri网Σ由模糊Petri网Σ1和Σ2同步合成的。假设t(1)i=t(2)i=ti即为公共变迁。则合成网Σ的输入矩阵I与输出矩阵O分别为I=
在实际应用中,根据复杂系统的特点,合成网的子网可以采用顺序连接,选择,重复,并行等不同组合方式进行组合,实现复杂系统的建模。
3 算例分析
Σ1和Σ2为模糊Petri网,变迁的阈值和流关系上的权值如图1所示。Σ1的初始标识为M10(0.8,0,0.7),Σ2的初始标识为 M20(0.9,0,0.8)。则 M0=(0.8,0,0.7,0.9,0,0.8),Σ 的输入矩阵 I与输出矩阵O分别为
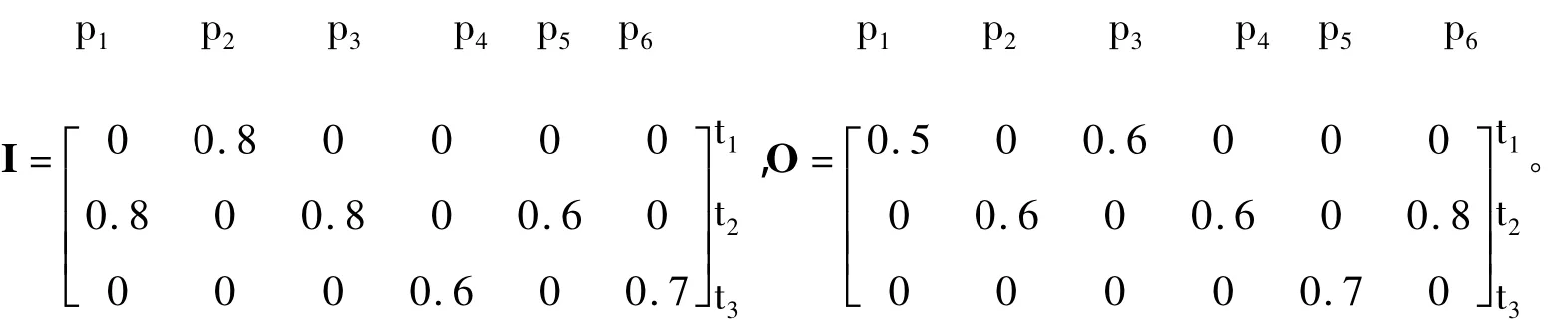
4 结束语
鉴于模糊Petri网的行为理论研究还处在起步阶段,缺乏有效分析工具,本文借鉴Petri网丰富的理论基础和分析方法,将合成运算扩展到模糊Petri网,研究了模糊Petri网的共享与同步合成运算,通过某些公共库所(共享合成)、公共变迁(同步合成)将两个简单模糊Petri网按合成规则组合成一个复杂的网系统,并利用子网的关系矩阵构造出合成网的矩阵。下一步将研究共享单链子网的模糊Petri网的合成及其应用研究。
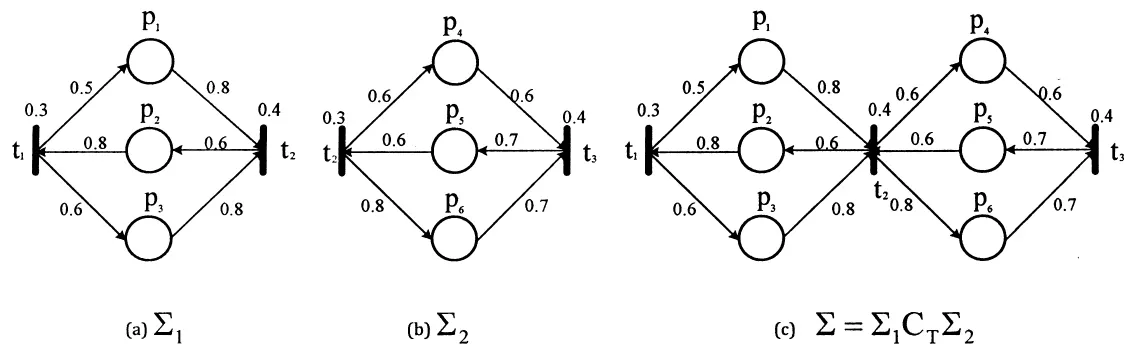
图1 同步合成网及其子网
[1] 王琦,韩江洪,王青山.Petri网合成理论及应用综述[J].计算机仿真,2008,25(12):8-11.
[2] 吴哲辉.Petri网导论[M].北京:机械工业出版社,2006:169-173.
[3] 贾立新,薛钧义,茹峰.采用模糊Petri网的形式化推理算法及其应用[J].西安交通大学学报,2003,37(12):1 263—1 266.
[4] 高梅梅,吴智铭.模糊推理Petri网及其在故障诊断中的应用[J].自动化学报,2000,26(5):677-680.
[5] Chen ShyiMing.Fuzzy backward reasoning using fuzzy Petrinetmodel[J].IEEE Transaction on system man and cybernetics-part B,2000,30(6):846-856.
[6] Looney CG.Fuzzy Petrinets for rule-based decision-making[J].IEEE Transactions on Systems,1988,18(1):178-183.
[7] Chengjia Li,Fuling Ding.Fuzzy Dynamic Petri Nets[C].Tianjin:Proceeding of Fifth International Conference on Fuzzy Systems and Knowledge Discovery,2009:14-16.

