关于周期函数定义的研究

潘劲松 童丽娟

(湖南机电职业技术学院人文科学系,中国 长沙 410151)

函数是一个非常重要的数学概念，它的定义为：给定两个实数集D和M，若有对应法则f，使对D内每一个x，都有唯一的一个数y∈M与它相对应，则称f是定义在数集D上的函数记为f(x)，x称为自变量．其中D称为f的定义域,记作D(f)，y的取值范围称为f(x)的值域．

周期函数是一类非常特殊的函数，表现在其图象每隔一段时间都要重复出现，具有循环往复直至无穷大的特点．但现实世界中某些具有周期性的运动是从某一时刻开始的，传统的周期函数的概念不足以刻画该类周期运动的规律性；另外，有些具有非常明显的周期特点的函数却不满足周期函数的经典定义[1-4]．因此，给具有周期性特点的函数一个全面的刻画显得非常重要．

以下讨论的函数都是实函数，我们用D(f)表示函数f(x)的定义域，R表示实数集合．InfD(f)表示D(f)的下确界，supD(f)表示D(f)的上确界．并且在该文中规定：当D(f)无下界时，规定InfD(f)=-∞，当D(f)无上界时，规定，supD(f)=+∞．

1 周期函数的几种传统定义

定义1[7]在加法群G上定义的函数f(x),如果对于某个ω∈G,f(ω+G)=f(x)对一切x∈G成立,则称ω为f(x)的周期.具有不等于0(G的单位元素)的周期的函数f(x)称为周期函数．

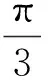
所以定义1作为周期函数的一般定义是不太妥当的．

定义2[5]对于函数f(x),如果存在常数l≠0，x∈D(f),有f(x+l)=f(x-l)=f(x)成立,那么称f(x)为周期函数,l为f(x)的一个周期．

定义2′[6]对于函数f(x),如果存在常数l≠0,每个x∈D(f)，有x±l∈D(f)且f(x+l)=f(x)成立,那么称f(x)为周期函数．

显然定义2与定义2′是等价的．

定义3[7]对函数f(x),如果存在常数l≠0,每个x∈D(f),有f(x+l)=f(x)成立,那么称f(x)为周期函数,l为f(x)的一个周期．

不难发现:

a) 定义2与定义3是不等价的, 定义2中周期函数的定义域是上、下无界的,而定义3中的周期函数的定义域可以是上、下有界的．

b) 定义2下的周期函数f(x)的图象,沿x轴任一方向,每隔l个单位(l为f(x)的周期),图象总是重复出现,而定义3下的周期函数． 沿x轴任一方向,每隔l个单位,它的图象都不一定能重复出现．

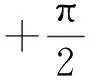
证(1)设函数f(x)是周期函数,l是它的一个周期,则任意x∈D(f),有sin(x+l)=sinx．

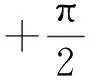
因此在定义3的意义下,f(x)是周期函数．

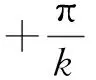
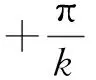
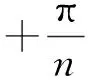
所以,定义3作为周期函数的定义是欠妥的．

定义4[8]设函数f(x)在R上有定义，若存在某个正数l使对于R上的任意x，x±l也在R上，且成立等式f(x±l)=f(x)，则称函数f(x)为周期函数，称l为周期函数f(x)的一个周期．

很容易看出在定义4的意义下定义的周期函数f(x)的定义域是上下无界的，但对于一些用于描述周期运动是从某点开始的函数来说，例如描述某一质点从0时刻开始做正弦运动的函数f(x)=sin(x),x≥0，它具有很强的周期性，但它却不满足定义4．所以定义4作为周期函数的一般定义也是不太理想的．

2 弱周期函数的定义、性质及定理

从上面的讨论可以得出：周期函数的传统定义1、2、3、4作为描述一般性周期运动的定义都是不太理想的，原因在于没有充分考虑到现实中描述周期运动的函数的定义域并不一定都是上下无界的.例如描述某一质点从某一时刻开始做周期运动的函数，它的定义域就是有下界的．所以需要有一个用来描述一般性周期运动的周期函数的新的定义,以此作为周期函数的传统定义的推广．

下面所讨论的函数如无特殊说明，其定义域可以是有下界无上界(形如(a,+∞)或[a,+∞))或有上界无下界(形如(-∞,a)或(-∞,a])．

定义5设f(x)是定义在R的子集上的函数,若存在周期为l的周期函数F(x)和区间T使得f(x)是F(x)在D(F)∩T上的限制, 即D(f)=D(F)∩T且每个x∈D(f)有f(x)=F(x),则称f(x)是弱周期函数.如果对每个x∈D(f),都有x+l∈D(f),称l是弱周期函数f(x)的周期．也就是说函数f(x)的图象是F(x)的图象在F(x)的定义域与I的交集上的部分，从某种意义上说函数f(x)是函数F(x)的一部分，所以弱周期函数是周期函数的推广．

通俗而言，只要函数图象呈现出一定的周期性，我们就说它是弱周期函数，并不要求它的定义域是上下无界的．

2.1 主要性质

由弱周期函数的定义,可得弱周期函数f(x)的如下简单性质:

(1) 弱周期函数的周期都是相应的周期函数的周期；

(2) 若l为弱周期函数f(x)的周期,则对任意n∈N,nl也是f(x)的周期；

(3) 若l为弱周期函数f(x)的周期,则函数f(x)的图象是周期函数F(x)的图象在无穷区间T上的相应部分,因此弱周期函数f(x)的图象沿x轴每隔l个单位(l<0时,沿x轴的负方向,每隔|l|个单位),其图象都能重复出现．

2.2 主要定理

定理1若f(x)是定义在R上的周期为l的周期函数，则f(x)也是周期为l的弱周期函数．

证因为f(x)是周期为l的周期函数，取F(x)=f(x)，则F(x)也是周期为l的周期函数，取T=D(F)=D(f)．显然有f(x)是周期函数F(x)在D(f)∩T上的限制，且x∈D(f)，有f(x)=F(x)．由此f(x)满足定理1，所以f(x)是弱周期函数，且它的周期为l．

从定理1可以看出：弱周期函数是周期函数的推广．

定理2设弱周期函数f(x)是周期函数F(x)在D(f)上的限制．

1)当D(f)无上界时,F(x)的每个正周期都是f(x)的周期；

2)当D(f)无下界时,F(x)的每个负周期都是f(x)的周期．

证(1)设l为F(x)的一个正周期．由于f(x)是弱周期函数，且f(x)是F(x)在D(F)上的限制，因此有右无穷区间T(形如(a,+∞)、[a,+∞)或(-∞,+∞))，使D(F)∩T．任意x∈D(f)，则x∈D(F)且[x,+∞)⊂T，所以x+l∈D(F)∩[x,+∞)⊂D(F)∩T=D(f)．因此l是f(x)的周期．同理可证明(2)．

从上面可以看出，当函数f(x)的定义域既无上界又无下界时，f(x)的弱周期性即函数的周期性．因此我们讨论函数的弱周期性，只要讨论函数的定义域为有下界无上界或有上界无下界两种情形.假定以下所讨论的函数的定义域都是有下界无上界的，且记函数定义域的下确界为a*．

设函数f(x)为弱周期函数，若a*∈D(f)，f(x)为周期函数F(x)在D(f)上的限制，则[a*,+∞)⊂T,[a*,+∞)∩D(F)⊂T∩D(F)=D(f)．又a*为D(f)的下确界，故D(f)⊂[a*,+∞)∩D(F)，从而D(f)=[a*,+∞)∩D(F)．

若a*∉D(f)，可类似推得：D(f)=(a*,+∞)∩D(F)．

由上面的分析，我们有下面的引理：

引理1 设弱周期函数f(x)是周期函数F(x)在D(f)上的限制．infD(f)=a*.

(1)若a*∈D(f),则D(f)=[a*,+∞)∩D(F)；(2)若a*∉D(f),则D(f)=(a*,+∞)∩D(F)．

定理3若f(x)为弱周期函数,则有常数l>0,每个x∈D(f),有f(x+l)=f(x)．

证由弱周期函数的定义，有周期函数F(x)，使D(f)=T∩D(F)(T为(a*,+∞)或[a*,+∞))，任意x∈D(f)，有f(x)=F(x)．

任取周期函数F(x)的一个正周期l，对x∈D(f)， 有x∈T且x∈D(F)，故x+l∈T且x+l∈D(F)，x+l∈D(f)， 因此f(x+l)=F(x+l)=f(x)．

定理4若f(x)为弱周期函数,l为它的一个正周期, infD(f)=a*,每个x∈(a*,+∞)-D(f),则x+l∈(a*,+∞)-D(f)．

证由x∈(a*,+∞)-D(f),则x∈(a*,+∞)且x∉D(f),故x∉D(F)．又l>0,所以x+l∈(a*,+∞)且x+l∉D(F),得x+l∉D(f),因此x+l∈(a*,+∞)-D(f)．

定理5(判定定理) 已知函数f(x),infD(f)=a*,则f(x)为弱周期函数的充要条件是:存在常数l>0,满足:

(1)每个x∈D(f),有f(x+l)=f(x);

(2)每个x∈(a*,+∞)-D(f),有x+l∈(a*,+∞)-D(f)．

证由定理2和定理3立即可得必要性.下面证明充分性．

(1)若a*∉D(f),如下构作以l为周期的周期函数F(x):

对任意x∈(a*,a*+l],当x∈D(f)时,令f(x)=F(x);当x∉D(f)时，则x∉D(F)．

设x∈D(F)∩(a*,+∞),则x∈D(F).由于F(x)是以l为周期的周期函数,有x0∈(a*,a*+l]和某个n0∈Z,n0≥0，使x=x0+n0l．据函数F(x)的定义,x0∈D(f)．

由定理的第一个条件,得x=x0+n0l∈D(f),从而

D(F)∩(a*,+∞)⊂D(f)．

(1)

设x∈D(f),则x∈(a*,+∞),存在x1∈(a*,a*+l]和n1∈Z,n1≥0,使x=x1+n1l．由定理的第二个条件,推得x1∈D(f),从而x1∈D(F),x∈D(F),x∈D(F)∩(a*,+∞),故

D(F)∩(a*,+∞)⟺D(f)．

(2)

由(1)、(2)两式:D(f)=D(F)∩(a*,+∞)．

对任意x∈D(f),已证明存在x1∈(a*,a*+l]和某个n1∈Z,n1≥0,使x=x1+n1l,且x1∈D(f)，从而f(x1)=F(x1)．由定理的第一个条件和l为周期函数F(x)的周期,有F(x)=F(x1+n1l)=F(x1)=f(x1)=f(x1+n1l)=f(x)．因此f(x)为弱周期函数．

(2)若a*∈D(f),只要在a*∉D(f)的证明中把区间(a*,a*+l]改成(a*,a*+l),把区间(a*,+∞)改成[a*,+∞)即可．

3 弱周期函数性质的简单应用

例3证明：f(x)是定义在上的非常值函数,有常数l>0,满足:任意x∈R,有f(x)=f(x-l)+f(x+l)成立,则函数f(x)是弱周期函数,且6l为它的一个周期．

证由已知条件可得

f(x+6l)=f(x+5l)-f(x+4l)=f(x+4l)-f(x-3l)-f(x+4l)=-(f(x+2l)-f(x+l))=

-(f(x+l)-f(x)-f(x+l))=f(x)

所以函数f(x)是周期函数,且6l为它的一个周期．根据定理1，得f(x)是弱周期函数,且6l为它的一个周期．

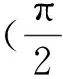
证若要证明函数f(x)不是周期函数，只要证明f(x)不是弱周期函数就可以了，用反证法．

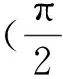
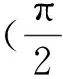
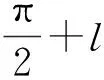
(3)

取正整数n0>l,x0=2n0π，则

|f(x)|=2n0π>π+l．

(4)

(3)与(4)矛盾，因此函数f(x)不是弱周期函数．从而f(x)也不是周期函数．

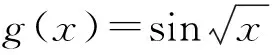
证同例3，若要证明函数f(x)不是周期函数，只要证明f(x)不是弱周期函数就可以了，用反证法．

若g(x)是弱周期函数，l是它的一个正周期，则对任意x≥0，有

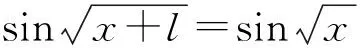
(5)

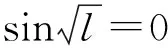
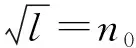
(6)

将(6)代人(5)，得：任意x≥0，有

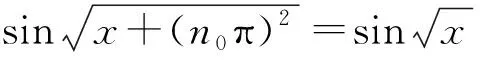
(7)

n02= 2k(2k+ 1).

(8)

证infD(h)=1,取l=1．

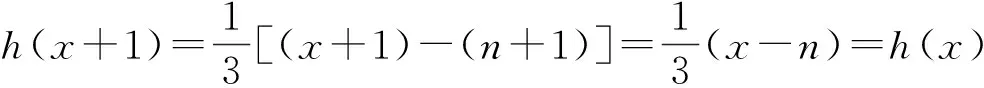
(2)设x∈(0,+∞)-D(h),则有n∈N，使x=n，所以x+1=n+1∉D(h)．

由定理5，h(x)为弱周期函数．

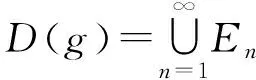
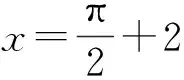
例8证明h(x)=tgx-tg(πx)不是周期函数．

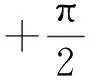
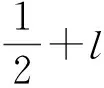
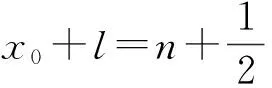
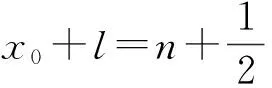
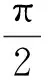
函数的弱周期性是函数的周期性的推广，如果函数在其定义域内具有一定的周期性(这里的定义域并不要求是上下无界的，可以是有下界无上界或有上界无下界，甚至可以是上下有界的)，就说它具有弱周期性．我们得出的结论是：函数满足周期性必定满足弱周期性；满足弱周期性并不一定满足传统的周期性的定义．因此函数弱周期性定义的适用范围比传统的函数周期性定义的适用范围要广，是周期函数的推广．

参考文献：

[1] 王印清,吴和琴.函数周期性初论[M].北京：高等教育出版社，1987.

[2] 张方盛,林伟华.谈谈周期性问题[J].数学通报,1984(10)：126-129.

[3] 田载今.周期函数定义的两种差异[J].数学通报,1989(1)：151-154.

[4] 刘兆庆.对周期函数的一些探讨[J].陇东学院自然科学学报，2003(10)：5-8.

[5] 宣立新,马 明.周期函数初论[M].合肥：安徽教育出版社，1989.

[6] Japanese mathematics weaved. Mathematics 100 section thesauruses[M]. Tokyo:Chapman and Hall Press,1984.

[7] 宣立新.高等数学[M].北京：高等教育出版社,1989.

[8] 华东师范大学数学系.高等数学[M].北京：高等教育出版社,2001.