非牛顿流体在多孔介质中渗吸现象的研究

王世芳, 吴涛,肖明

(1.湖北第二师范学院物理与电子信息学院,湖北 武汉 430205；2.武汉工程大学理学院,湖北 武汉 430074)

渗吸是润湿相流体在多孔介质中主要依靠毛细力作用置换另一种非润湿相流体的物理过程.渗吸是一种常见物理输运现象,广泛存在于土壤学、石油工程、纤维材料等一些相关实际应用领域.毛细上升是一种基本的物理现象,广泛存在于自然过程及人类活动中.毛细效应在化学工程、冶金技术、地下水工程、石油工程、纺织物干燥等领域中也具有重要作用[1-3],尤其是在多孔介质渗吸中起着不可估量的作用,如利用自发渗吸驱油已成为低渗裂缝油藏采油的一个重要机理[4].因此,依靠毛细力产生的渗吸现象越来越来越受到关注.

目前,大部分研究者主要研究牛顿流体在多孔介质中的流动特性和传输现象,但是在自然资源恢复与储存工程等地表系统中,非牛顿流体却处处存在.因此,研究非牛顿流体在多孔介质中流动行为对实际工程应用领域是十分非必要的.Bingham流体是一种常见的非牛顿流体,这种流体仅当剪切应力超过某一有限值时才开始流动,这有限应力值τ0称为该流体的屈服应力.

Roquet和Saramito[5]用有限单元方法模拟了圆柱体中宾汉姆流体的流动.Balhoff和Thompson[6]也用有限单元方法模拟了轴对称收缩管道中宾汉姆流体的流动.1921年,Washburn[7]给出了水在单根毛细管中渗吸高度及渗吸质量随时间变化的解析表达式.他的模型认为多孔介质是由直径相同、并列排列的毛细管组成的.然而,大量的实验证明,多孔介质的孔隙是呈分形结构且孔隙空间在3-4个数量级的范围内是自相似的,孔隙大小在1 nm至100 μm内变化.Benavente[8]等人通过引入迂曲度和孔形状等描述多孔介质的微结构参数对LW方程进行了修正.在他们的模型里,迂曲度等于3,是一经验常数,不具有明确的物理意义,且他们的模型预测与实验数据吻合得不好. Cai[9]等人基于多孔介质的分形特征提出了牛顿流体在多孔介质中的自发顺向渗吸的分形模型,并得到了牛顿流体在多孔介质中渗吸高度与渗吸质量的解析表达式.本文中主要研究了非牛顿Bingham流体在毛细力作用下在多孔介质中的渗吸现象,得到了非牛顿Bingham流体渗吸高度与渗吸质量的分形解析表达式.

1 理论模型

(1)

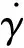
(2)

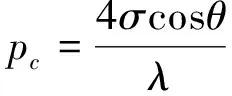
(3)

(4)

大量实验证明多孔介质的孔隙大小的分布满足分形分布,孔隙直径在λ到λ+dλ区间里的孔隙数目：

(5)

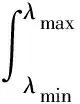
(6)

满足分形分布的多孔介质孔隙面积为：

(7)

(8)

(9)

Bingham流体在多孔介质中渗吸上升的平均流速可以表示为：

(10)

多孔介质内流体流动通道的实际平均长度[ 12-13]：

(11)

(12)

(13)

联立(10)式和(13)式得到渗吸高度随时间的变化关系：

(14)

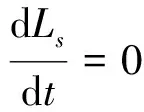
(15)

(15)式表明渗吸所能达到的平衡高度与多孔介质的结构特征(DT,Df,λmax和β)、液体的流变特性(密度ρ、粘度μ、屈服应力τ0)有关.

Bingham湿润液体吸入到多孔介质的质量随时间的变化关系可以通过下面积分得到：

(16)

(17)

将(14)式代入到(17)式并应用(16)式可得：

(18)

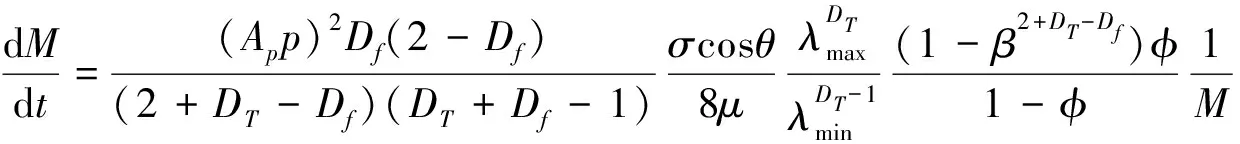
(19)

(19)式代表了在渗吸初期忽略重力因素情况下,牛顿流体在多孔介质中累积渗吸质量与时间的关系.代入初始条件M(0)=0,并对(19)式积分得到：

(20)

(20)式表明在渗吸初期,多孔介质中渗吸的牛顿流体质量M与时间的平方根t1/2成正比,这与cai[13]等人得出的结论相一致.

2 结果分析

由于大部分多孔介质孔隙分布具有分形特征,因此可以把多孔介质看作是由一束独立的、不同尺寸、彼此不相交的毛细管组成.考虑毛细管迂曲度,研究非牛顿Bingham流体在多孔介质中渗吸的物理机制,包括其上升高度和上升质量随时间的变化.

多孔介质的孔隙分形维数可以由(8)式确定.多孔介质的最大孔隙直径可以采用颗粒呈等边三角形排列的模型和颗粒呈正方形排列的模型所得的最大孔隙直径的算术平均值[13],即

(21)

ds为固体颗粒直径,在文中取ds=0.02 cm,φ为多孔介质的孔隙率.

本文中选取Bingham流体的流变特性参数如下：密度ρ=1.00×103kg/m3,稠度系数μ=0.001 Pa·s.表面张力σ=72.7×10-3N/m,接触角θ°=π/6,多孔介质的孔隙率φ=0.4,迂曲度分形维数DT=1.1.一旦多孔介质的孔隙率φ给定,分形维数Df就可以由(8)式确定.

图1为基于(14)式,考虑非牛顿Bingham流体的重力因素后,Bingham流体在多孔介质中渗吸高度随时间的变化关系.从图1可以看出,在渗吸的初期,Bingham流体在多孔介质中上升的速度比较大,然后速度逐渐减小直至达到平衡高度.图1还说明了屈服应力对渗吸的平衡高度有一定的影响,渗吸的平衡高度随屈服应力的减小而增大.

基于(10)式,图2显示了不考虑重力因素下,流体流变特性τ0=0时,流体在多孔介质中渗吸累积质量与渗吸时间平方根呈线性关系.这与Lucas-Washburn方程是一致的,也与Cai[13]等人得到的结论一致.

图3是基于(18)式,考虑Bingham流体的重力因素后,Bingham流体在多孔介质中累积质量随时间的变化关系.从图3可以看出,在渗吸初期,流体在多孔介质中的渗吸速度很快,然后速度逐渐减小,以至于Bingham流体在多孔介质中渗吸总质量基本保持不变而趋近于平衡.另外,图3还反映了屈服应力τ0越大,多孔介质中渗吸流体质量越少,这是因为屈服应力越大,Bingham流体受到的粘滞阻力越大,因此渗吸到多孔介质中流体质量就越少.

图1 考虑重力作用时渗吸高度随时间的变化关系

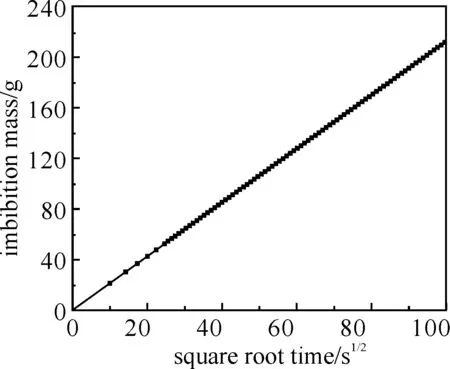
图2 不考虑重力因素时渗吸质量与时间的关系

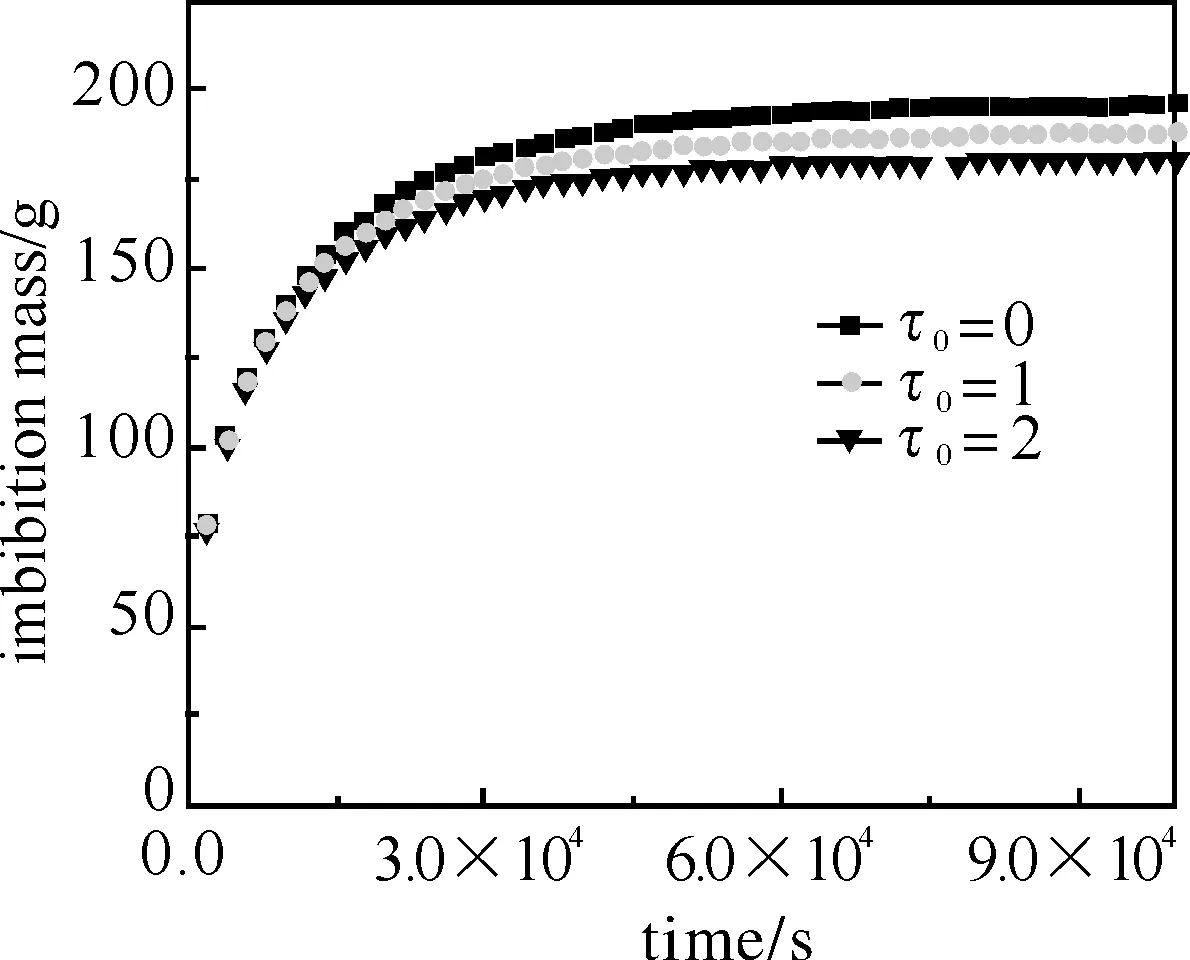
图3 考虑重力因素时渗吸质量与时间的关系

3 结论

本文中提出一种关于非牛顿Bingham流体在多孔介质中发生渗吸的简单分形模型,其渗吸高度及渗吸质量不仅与Bingham流体的流变特性(粘度、屈服应力、密度)有关,还与多孔介质的微结构参数(分形维数、最小孔隙直径、最大孔隙直径)有关.结果表明在渗吸初期,渗吸速度比较大,然后渗吸速度逐渐减慢直至达到到平衡状态；屈服应力τ0越大,Bingham流体在多孔介质中渗吸高度与渗吸累积质量越小.此结论可能为低渗透油藏中提高石油采油产量提供一定的理论指导意义.

[1] Abraham Marmur, Cohen Ruben D. Characterization of porous media by the kinetics of liquid penetration：the vertical capillaries model[J].Journal of Colloid and Interface Science,1997,189(2):299-304.

[2] Pezron I , Bourgain G, Quere D. Imbibition of a fabric[J].Journal of Colloid and Interface Science,1995,173(2)：319-327.

[3] Zhmud B V, Tiberg F,Hallstensson K. Dynamics of capillary rise[J].Journal of Colloid and Interface Science,2000,228(2):263-269.

[4] Cuiec L E, Bourbiaux B, Kalaydjian F. Oil recovery by imbibition in low-permeability chalk[J].SPE Form Eval,1994,9(3)：200-208.

[5] Roquet N, Saramito P. An adaptive finite element method for Bingham fluid flows around a cylinder[J].Comput Meth Appl Mech Eng,2003,192(31):3317-3341.

[6] Balhoff M T, Thompson K E. Modeling the steady flow of yield stress fluids in packed beds[J].AICHE J,2004,50(12)：3034-3048.

[7] Washburn E W. The dynamics of capillary flow[J].Phys Rev,1921,17(3):273-283.

[8] Benavente D, Lock P,geles García Del Cura M, et al. Predicting the capillary imbibition of porous rocks from microstructure[J].Transp Porous Media,2002,49(1)：59-76.

[9] Cai Jianchao, Yu Boming, Mei Maofei, et al. Capillary rise in a single tortuous capillary[J].Chin Phys Lett,2010,27(5):054701-1-4.

[10] Bird R B, Stewart W E, Lightfoot E N. Transport phenomena[M].New York:John Wiley & Sons Inc,1960:11-20.

[11] Yu Boming, Li Jianhua. Some fractal characters of porous media[J].Fractals,2001,9(3):365-372.

[12] Yu B M, Cai J C, Zou M Q. On the physical properties of apparent two-phase fractal porous media[J].Vadose Zone J,2009,8(1):177-186.

[13] Cai Jianchao, Yu Boming, Zou Mingqing, et al. Fractal characterization of spontaneous co-current imbibition in porous media[J].Energy Fuels,2010,24:1860-1867.