几类二元等重码的构造

周四维,张莉,李跃新

(1.湖北大学知行学院,湖北 武汉 430011；2.湖北大学数学与计算机科学学院,湖北 武汉 430062)

等重码,尤其是二元等重码在纠错码理论和通信理论中都有着重要的应用,如它在差错控制系统(ARQ)[1-2]中的应用.作为一种检测码,其应用非常简单,在检测中只需检测接受到码字中1的数目就可确定传输是否正确.

一个参数为(n,M,d,w)的等重码指的是一类码字的长度为n,所含码字的个数为M,码字之间的极小汉明距离为d且每个码字的汉明重量均为w的码.关于等重码的研究,主要涉及到3个方面的问题.其一是关于等重码的构造,即如何构造参数为(n,M,d,w)的等重码.其二是对于给定的参数为(n,d,w)的等重码,确定其理论上存在的码字个数的理论界.一般地,这个理论上存在的码字最大个数记为A(n,d,w).其三是在前一问题的基础上确定A(n,d,w)的具体值并构造出相应参数的码.相对于等重码的构造而言,码所含码字个数的研究比较困难.如果等式M=A(n,d,w)成立,则称一个该参数为(n,M,d,w)的等重码是最优的.关于等重码的构造,可参见文献[3-6],其中亦包含一些最优等重码.而关于等重码的码字个数的理论界,可参见文献[7-8].至于A(n,d,w)的具体值的研究,可参考文献[9].

本文中主要讨论二元等重码的构造并分析所得码是否是最优这两个方面的问题.首先通过差集和几乎差集所对应的序列来构造等重码,并详细讨论所得等重码的各个参数.考虑到差集所对应序列具有两值自相关性以及几乎差集对应三值自相关序列,并给出一个基于单条序列的等重码的一般构造方法.这是本文中的第一部分,即等重码的构造.第二部分即是分析上述所构造的等重码的最优性问题.从这一部分的讨论可以知道,在这类构造中,从码字的个数来看,基于差集构造出的等重码较之其他几类要好些,这是由构造方法所决定的.并且,从中得到了一类最优等重码.需要说明的事,这类码的参数不全是新的,其中只有部分是新的.另外,有些码的参数虽然不是新的,但对应的码字是新的.

1 预备知识

1.1码的参数介绍对于一个长度为n的码x=(x1,x2,…,xn),它的汉明重量wt(x)定义为码字中非零元的个数,即wt(x)=|{i:xi≠0,1≤i≤n}|.两个码字之间的汉明距离则定义为

d(x,y)=|{i:xi≠yi,1≤i≤n}|,

其中y=(y1,y2,…,yn).若x和y都是二元码,则d(x,y)=wt(x⊕y),其中⊕表示模2运算.

设C是一个含有M个码字的码,即C={ci:1≤i≤M},码C的极小距离定义为

d=min{d(ci,cj):ci,cj∈C,i≠j}.

码的极小距离是一个非常重要的概念,它与码的纠错能力密切相关.比如对于一个分组码来说,若要在码字内检测出d个随机错误,则要求码的极小距离至少是d+1；若要码字内纠正d个随机错误,则要求码的极小距离至少是2d+1[3].

1.2 序列的相关函数

定义1设a={a(0),a(1),…,a(N-1)}和b={b(0),b(1),…,b(N-1)}是两个周期为N的二元序列,它们之间的周期相关函数在移位0≤τ≤N-1处的定义为

其中i+τ为模N运算.

1.3循环差集差集与序列,尤其是二元最优序列之间具有紧密的联系.在这一小节中,我们主要介绍循环差集和几乎差集的概念以及它们的一些简单性质.

定义2设G是一个阶为υ的加法群,令D={d1,d2,…,dk}.如果G中每一个非零元在多重集{d1-d2:d1,d2∈D,d1≠d2}中恰好出现λ次,则称D是一个参数为(υ,k,λ)的差集.特别地,如果G为循环群Zυ=Z/υZ,那么称D是一个参数为(υ,k,λ)的循环差集.

差集是一个重要的数学工具.在本文中,我们只需用到差集的一些简单性质.更多关于差集的叙述可参见文献[10].

引理1[10]设D={d1,d2,…,dk}是一个参数为(υ,k,λ)的循环差集,则有k(k-1)=(υ-1)λ,且D的补集是一个参数为(υ,υ-k,υ-2k+λ)的循环差集.

定义3设(A,+)是一个阶为n的Abel群,令S={s1,s2,…,sk}.当w取遍A中所有非零元时,如果|{s+w:s∈S}∩S|等于λ总共出现μ次以及等于λ+1总共出现n-1-μ次,则称S是一个参数为(υ,k,λ,μ)的几乎差集.

与差集类似,几乎差集也有类似于引理1的性质,在此不再详述.

2 二元等重码的构造

(1)

对由差集构造的上述二元序列s,它的自相关函数是两值的,具体结论如下.

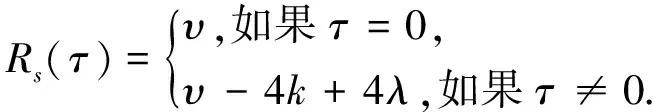
根据上面的引理,我们首先可以通过如下方式构造一类等重码.

构造1设序列s由参数为(υ,k,λ)的差集如(1)式所定义,且令L为左循环移位算子,即Li(s)=(si,si+1,…,si-1),其中下标进行的是模υ运算.定义集合C1={Lτ(s):0≤τ≤υ-1}

(2)

基于构造1得到的等重码具有以下性质.

定理1如(2)式定义的集合C1构成一个参数为(υ,υ,2k-2λ,υ-k)的二元等重码.

定理1的证明根据序列s和集合C1的定义,C1中的码字的长度为υ,码字的汉明重量为υ-k,且集合C1所含有的码字个数为υ.因此,我们只需讨论C1中码字之间的距离.任取C1中的两个码字c1=Lτ1(s),c2=Lτ2(s),0≤τ1,τ2≤υ-1.于是,C1和C2之间的汉明距离为d=wt(Lτ1(s)⊕Lτ2(s)).

不失一般性,假设τ2>τ1,则由移位算子L的定义不难验证

d=wt(Lτ1(s)⊕Lτ2(s))=wt(s⊕Lτ2-τ1(s)).

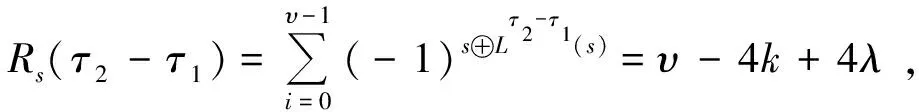
继而可得 (υ-wt(s⊕Lτ2-τ1(s)))-wt(s⊕Lτ2-τ1(s))=υ-4k+4λ,

即d=wt(s⊕Lτ2-τ1(s))=2k-2λ,

证毕.

通过序列的自相关函数,我们还可以通过以下方式构造出另一类等重码.

构造2设序列s由参数为(υ,k,λ)的差集如(1)式所定义,且令L为左循环移位算子,定义集合

C2={s⊕Lτ(s):Rs(τ)=υ-4k+4λ,1≤τ≤υ-1}

(3)

对于上述定义的集合C2,我们可以证明以下结论.

定理2如(3)式定义的集合C2构成一个参数为(υ,υ-1,2k-2λ,2k-2λ)的二元等重码.

定理2的证明由集合C2的定义可知,C2中含有一个υ-1个码字且码字的长度为υ.任务C2中的一个码字C=s⊕Lτ(s),1≤τ≤υ-1.不妨设C的汉明重量为w,则根据序列s的自相关函数值可得

即有w=wt(c)=2k-2λ.因此,下面我们需要证明C中码字之间的极小距离也是2k-2λ.任取C2中的两个码字c1=s⊕Lτ1(s),c2=s⊕Lτ2(s),1≤τ1,τ2≤υ-1.于是,结合码字之间距离的定义可知,C1和C2之间的汉明距离为d=wt(s⊕Lτ1(s)⊕s⊕Lτ2(s))=wt(Lτ1(s)⊕Lτ2(s)).

仍然假设τ2>τ1,则可验证d=wt(Lτ1(s)⊕Lτ2(s))=wt(s⊕Lτ2-τ1(s)).

故而,类似前面关于码字重量的讨论,有d=2k-2λ.证毕.

推论1若υ=3k-2λ,则C2∪{s}构成一个参数为(υ,υ,2k-2λ,2k-2λ)的二元等重码.

推论1的证明由序列s的定义,即(1)式可知,wt(s)=υ-k.所以结合已知条件υ=3k-2λ可知,wt(s)=υ-k=2k-2λ.另一方面,s与C2中码字之间的距离为

d=wt(s⊕s⊕Lτ(s))=wt(Lτ(s))=wt(s).

于是,再根据定理2可知上述推论成立.证毕.

对于一个参数为(υ,k,λ)的差集,由引理1有(υ-1)λ=k(k-1),再结合条件υ=3k-2λ,消去参数υ可解得k=2λ+1或k=λ,其中解k=λ需舍弃,否则得到υ=k=λ,所以代入k=2λ+1,有υ=4λ+3,即推论1中对应的差集参数为(4λ+3,2λ+1,λ).注意到此时Rs(τ)=υ-4k+4λ=-1,即序列s是一个理想两值自相关序列.

需要说明的是,在一定条件下,C1和C2∪{s}是一致的.为了得到不同类的码,下面我们给出C1和C2∪{s}不等价的条件.为此,我们需要以下定义.

定义4对于一个周期为N的二元序列s,我们称序列s具有三项式特性,如果对任一i,1≤i≤N-1,均存在一个j,1≤j≤N-1使得s⊕Li(s)=Lj(s)成立.

比如,m序列就是一个具有三项式特性的序列.事实上,具有三项式特性的序列并不多.而且,具有理想两值自相关的序列不一定就具有三项式特性.

关于构造1和构造2之间的关系,我们有

命题1对于构造1和构造2中的序列s,若s具有三项式特性,则C1和C2∪{s}是同一码；否则,则C1和C2∪{s}是不同的两种码.

上述构造1和构造2都是从两值自相关序列而来,通过自相关函数取值的分布性质,从不同的组合方式来构造等重码.构造的关键是两值自相关序列,本质是差集.自然地,我们想知道,如果(1)式的定义中,集合D是一个几乎差集,结果会是怎样呢？我们是否可以构造新的等重码？

类似地,与引理2一样,我们有下面的引理.

引理3[11]设二元序列s=(s0,s1,…,sυ-1)是由参数为(υ,k,λ,μ)的几乎差集D定义的如(1)式的序列,则序列s的自相关函数是三值的,且当τ取遍{0,1,…,υ-1}时,自相关函数的分布为

构造3设序列s由参数为(υ,k,λ,μ)的几乎差集如(1)式所定义,且令L为左循环移位算子,定义集合C3={Lτ(s):0≤τ≤υ-1}

(4)

结合引理3,我们可证明下面的结论.

定理3如(4)式定义的集合C3构成一个参数为(υ,υ,d,υ-k)的二元等重码,其中d≥2k-2λ-2,且码字之间的距离是2k-2λ或者是2k-2λ-2.

定理3证明由序列s的定义,集合C3中的码字长度为υ,码字的汉明重量为υ-k且C3中含有的码字个数为υ.下面,我们讨论C3中码字之间的距离.任取C3中的两个码字c1=Lτ1(s),c2=Lτ2(s),τ1≠τ2且0≤τ1,τ2≤υ-1.于是,C1与C2之间的汉明距离为

d=wt(Lτ1(s)⊕Lτ2(s)).

类似于定理1中的讨论,结合序列的自相关函数即引理3,不难得到

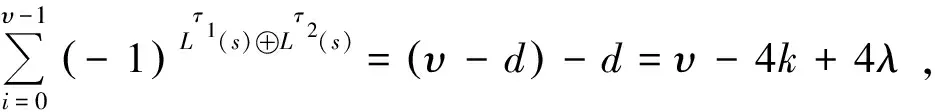
d=2k-2λ,或d=2k-2λ-2.

证毕.

与差集对应的序列类似,利用几乎差集定义的序列也能用来构造形如

的二元等重码.

类似于定理2 的证明,我们可得到如下结论.

从上面的构造可以看出,通过差集或者是几乎差集可以构造出不同参数的二元等重码.事实上,从序列的角度来看,基于序列的自相关性,也可以构造二元等重码.而且,可以将上面的构造推广到一般情形.

设二元序列s=(s0,s1,…,sυ-1),且当τ取遍{0,1,…,υ-1}时,自相关函数的分布为

(5)

构造4设二元序列s的自相关函数满足(5)式,定义集合C4={Lτ(s):0≤τ≤υ-1}

(6)

类似于定理3的证明,不难得到如下结论.

定理4设u=max{u1,u2,…,um},则如(6)式定义的C4构成一个参数为(υ,υ,d,w)的二元等重码,其中w=wt(s)且d≥(υ-u)/2.

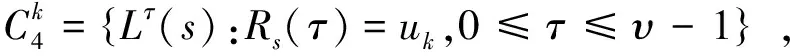
则也有如下类似结果.

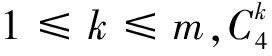
3 码的参数分析及实例

对于一个给定参数为(n,M,d,w)的等重码,它的最优性的讨论是一个比较困难的问题.首先,需要找到合适的关于A(n,d,w)的理论上界.对于不同参数的(n,d,w)等重码,人们从不同角度讨论了A(n,d,w)的理论上界,也得到了一些结果,如Plotkin界[12],Johnson界[7]等.其次,需要证明M=A(n,d,w).在这一节中,我们引用非递归的Johnson界[7]或文献[13]中讨论常复合码的界来分析上一节中所构造出来的等重码,因为对于二元而言,常复合码实际上就是等重码.

引理4[14]对于一个参数为(n,d,w)的二元等重码,如果nd-2nw+2w2>0,则

下面我们就用这个理论界来分析第2部分中所构造出来的部分等重码.

设D是一个参数为(υ,k,λ)的循环差集,且满足条件υ-4k+4λ=-1.则由定理1可知,此时C1构成一个参数为(υ,υ,2k-2λ,υ-k)的等重码.根据命题1有k(k-1)=λ(υ-1),再结合条件υ-4k+4λ=-1可得υ=2k+1或者υ=2k-1.于是可讨论如下情形.

(1)若υ=2k+1.此时有(υ,k,λ)=(4λ+3,2λ+1,λ).于是

nd-2nw+2w2=υ(2k-2λ)-2υ(υ-k)+2(υ-k)2=2(λ+1)>0.

另一方面,由定理1可知,参数为(υ,υ,2k-2λ,υ-k)的等重码已构造出来,由定义即有A(n,d,w)≥υ,因此A(n,d,w)=υ.故而此时C1是最优的.

(2)若υ=2k-1.此时有(υ,k,λ)=(4λ-1,2λ,λ).从而

nd-2nw+2w2=υ(2k-2λ)-2υ(υ-k)+2(υ-k)2=2λ>0.

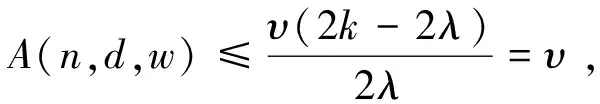
类似(1)可知A(n,d,w)=υ.故而此时C1是最优的.

命题2设D是一个参数为(υ,k,λ)的循环差集,且满足条件υ-4k+4λ=-1.则由构造1得到的等重码C1是最优码.

因υ-4k+4λ=-1,由引理2,此时对应的即是二元理想两值自相关序列.从序列的角度,比如m序列,一些相应的最优二元等重码已经构造出来.因此命题2中所得到的最优二元等重码在参数上并不都是新的.再结合命题1可知,若差集对应的二元序列不具有三项式特性,则等重码C2∪{s}不同于C1且是最优的,更重要的是,C2∪{s}中的码字之间不循环等价.值得考虑的是,对于υ-4k+4λ≠-1的情况,是否会得到最优二元等重码？

例1设D是一个参数为(2n-1,2n-1,2n-2)的Singer差集,则由构造1得到的是参数为(2n-1,2n-1,2n-1,2n-1-1)的最优等重码.

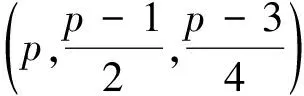
例3设D是一个参数为(4N,2N,N-1,N)的几乎差集,则基于(1)式定义的序列的自相关分布满足条件

于是由构造3可知,C3此时是一个参数为(4N,4N,2N,2N)的二元等重码.验证可知,这类码不能用引理4来判定它是否最优.这类码的参数比较特殊,它的最优性与4N阶Hadamrd矩阵的存在与否有着密切的联系,见文献[14].如果不存在4N阶Hadamrd矩阵,这类码能否达到最优尚不可知.

4 结论

本文中主要给出了几类基于单个序列构造的二元等重码,并结合码的定义和序列的自相关性确定了码的各个参数.通过分析码的最优性表明,序列自相关函数取值个数越少,所构造的等重码的参数可能就会越好.结合已有的理论界,我们证明了基于理想两值自相关序列构造的等重码可以达到最优.对于其他情况,是否还能找到最优等重码尚不可知,这是下一步要研究的问题.

[1] Wang X M,,Yang Y X.On the undetected error probability of nonlinear binary constantweight codes[J].IEEE Trans Commu,1994,42(7):2390-2393.

[2] Fu F W,Xia S T.Binary constant weight codes for error detection[J].IEEE Trans Inform Theory,1998,44(3):1294-1299.

[3] MacWilliams F J,Sloane N J.The theory of error-correcting codes[M].Amsterdam,The Netherlands:North-Holland,1977.

[4] Chee Y M,Ling S. Constructions for q-ary constant-weight codes[J].IEEE Trans Inform Theory,2007,53(1):135-146.

[5] Fu F W,Han Vinck A J,Shen S Y.On the construction of constant-weight codes[J].IEEE Trans Inform Theory,1998,44(1):328-333.

[6] Zeng F X. Properties ofm-sequence and construction of constant weight codes[J].IEICE Trans Fundamentals,2005, E88-A(12):3675-3676.

[7] Johnson S M.A new upper bound for error-correcting codes[J].IEEE Trans.Inform.Theory,1962,8(3):203-207.

[8] Agrell E,Vardy A,Zeger K.Upper bounds for constant-weight codes[J].IEEE Trans Inform Theory,2000,46(7):2373-2395.

[9] Brouwer A E,Shearer James B,Sloane N I A,et al.A new table of constant weight codes[J].IEEE Trans Inform Theory,1990, 36(6):1344-1380.

[10] Baumert L D.Cyclic difference sets[M].New York:Springer-verlag,1971.

[11] Arasu K T,Ding C,Helleseth T,et al. Almost difference sets and their sequences with optimal autocorrelation[J].IEEE Trans Inf Theory, 2001,47(7):2934-2943.

[12] Ploktin M.Binary codes with specified minimum distance[J].IEEE Trans Inf Theory, 1960,6(4):445-450.

[13] Luo Y,Fu F W,Vinck A J H,et al.On constant composition codes overZq[J].IEEE Trans Inf Theory,2003,49(11):3010-3016.

[14] Semakov K V,Zinoviev V A.Balanced codes and tactical configurations(in Russian)[J].Probl Peredach Inform,1969,5(3)：28-37.