分段连续型微分方程θ-方法的散逸性

王琦

(广东工业大学应用数学学院, 广东 广州 510006)

0 引言

分段连续型微分方程是延迟微分方程的一个重要分支,是对很多系统进行建模的重要工具.自变量的分段连续性不仅刻画了动力系统的连续性和稳定性,也反映出系统的振动性和周期性,因此,这类方程在差分方程的研究中起着重要作用,进而能更有效地解决一些包含离散和连续变量的混合系统中的问题, 如神经网络[1], 人口模型[2]等. 近20年来, 分段连续型微分方程引起了人们的普遍关注, 对于这类方程的解析解的研究已经非常深入,主要涉及稳定性[3]、周期性[4]、存在唯一性[5]和积分流形的存在性[6]等几种重要性质,而对这类方程自身的全面阐释和系统分析,可以参考文献[7].

虽然对于分段连续型微分方程解析解的研究已有大量结果, 但是对其数值解的研究却相对滞后, 不过发展很快. Liu等[8]和Song等[9]分别研究了这类方程中带有延迟项[t]和[t+1]的Runge-Kutta方法和θ-方法的稳定性,得到了解析解的渐近稳定区域包含在数值解的渐近稳定区域的充分必要条件. 在文献[10-11]中, 作者针对带有延迟项[t-1]的分段连续型微分方程,分别研究了θ-方法和Runge-Kutta方法的振动性,获得了数值方法保持方程本身振动性的充分必要条件. 在这类方程数值解的散逸性研究方面有一些研究[12-13].不同于文献[12-13],本文中主要研究一般情形下带有一个延迟项[t]的分段连续型微分方程θ-方法的散逸性, 给出两种θ-方法散逸的充分条件.

设〈·〉为定义在Hilbert空间X上的内积,‖·‖为从属范数. 本文中考虑下述分段连续型微分方程

(1)

其中[·]表示最大取整函数, 局部Lipschitz连续函数f:[0,+∞)×X×X→X满足

Re〈u,f(t,u,v)〉≤ω(t)+p(t)‖u‖2+q(t)‖v‖2,u,v∈X,t≥0

(2)

这里的p(t),q(t)和ω(t)是连续函数. 这类方程的一般形式为

x′(t)=f(t,x(t),x(α(t)))

(3)

其中α(t)是分段连续函数. 根据文献[7],有下面的定义.

定义1满足下列条件的连续函数x(t)称为方程(1)式在区间[0,+∞)上的解,

(i)x′(t)在[t]∈[0,+∞)的这些点处存在单侧导数,在t∈[0,+∞)的其他点处存在导数；

(ii)在每个区间[n,n+1)⊂[0,+∞)上,x(t)满足方程(1)式.

在后面的部分,我们将讨论方程(1)式的θ-方法的数值散逸性,并给出相关结论.

1 解析解的散逸性

散逸性是动力系统所研究的诸多问题中的重要方面. 所谓散逸性,就是系统具有一有界吸引集,从任意初始条件出发的解经过有限时间后进入该吸引集并随后保持在里面. 当用数值方法求解系统时,人们希望数值解也能具有散逸性,即数值散逸性的保持问题. 本文中将主要探讨θ-方法对分段连续型微分方程(1)式散逸性的保持问题.

下面的定义精确地描述了散逸性.

定义2[12]称方程(1)式在集合H上是散逸的,如果存在一个有界集B⊂H, 使得对于任意的有界集Φ⊂H都存在时刻t0=t0(Φ), 只要初值x0∈Φ, 则当t≥t0时相应的解x(t)∈B,B称为H中的一个吸引集.

为简便起见,在下文始终令不等式(2)式中的函数p(t),q(t)和ω(t)为常数,即

p(t)≡p,q(t)≡q,ω(t)≡ω,

那么,不等式(2)式化为 Re〈u,f(t,u,v)〉≤ω+p‖u‖2+q‖v‖2,u,v∈X,t≥0

(4)

下面的定理给出了方程(1)式的解析解为散逸的充分条件.

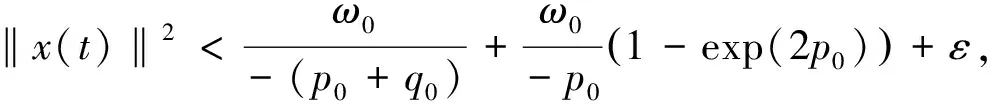
即系统是散逸的. 对任意的ε>0,开球

2 线性θ-方法的数值散逸性分析

取步长h=1/m(m≥1), 节点tn=nh(n=1,2,…), 将线性θ-方法应用于方程(1)式得

(5)

(6)

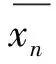
定义3称数值方法(6)式是散逸的,如果存在一个常数r, 使得对于任意的初值x0,都存在n0=n0(h,x0), 当n≥n0时有‖yn‖≤r.

下面给出本文中的第一个主要定理.

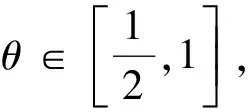
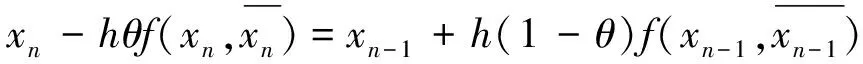
(7)

将(7)式的两侧同时与自身作内积得

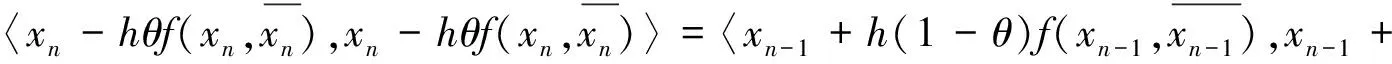
(8)

(9)

移项有

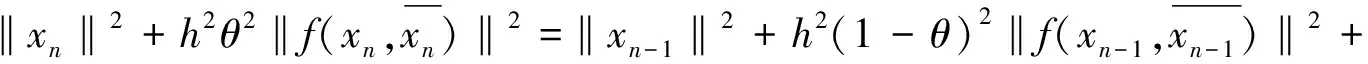
(10)

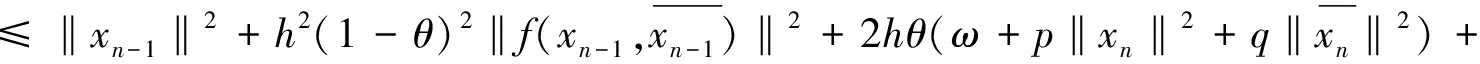
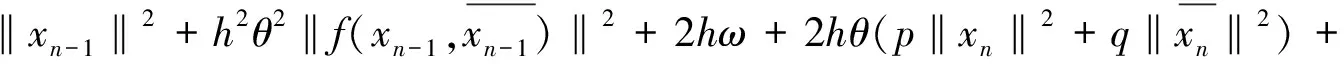
(11)

再由数学归纳法得

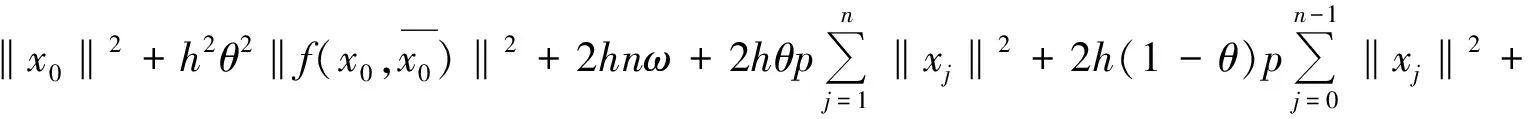
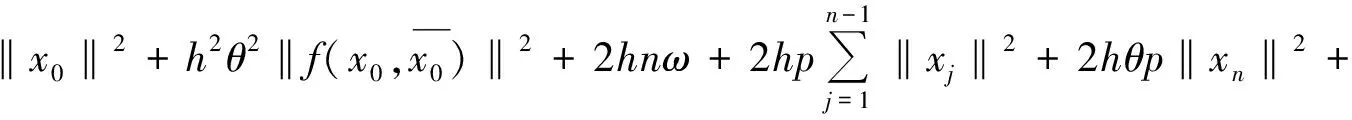
(12)

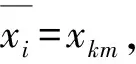
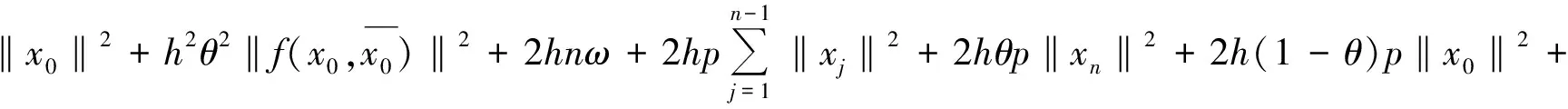
2hnq‖xkm‖2≤

L0+2hnω+[2hp(n-1)+2hθp+2h(1-θ)p+2hnq]L1=

L0+2hnω+2hn(p+q)L1

(13)

其中

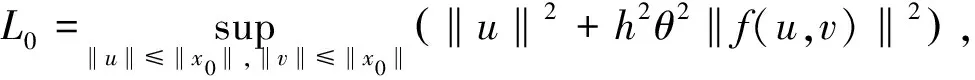
故,当p+q≥0时有

‖xn‖n0,

证毕.

3 单腿θ-方法的数值散逸性分析

步长的取法如第2节所示, 将单腿θ-方法应用于方程(1)式得

(14)

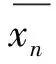
下面给出第二个主要定理.

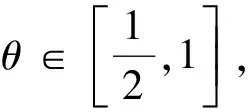
定理3的证明为了行文简便,令

(15)

(16)

由(15)式和(16)式得

yn+1-yn=θ(xn+1-xn)+(1-θ)(xn-xn-1)

(17)

又由(14)式得

(18)

即

(19)

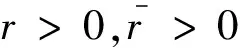
由定理2和定理3不难看出,两种θ-方法具有相同的散逸性, 这与考虑稳定性时得到的结论一致.

4 结论

用两种θ-方法分别求解一类典型的分段连续型微分方程, 利用不等式放缩等技术方法分析了数值格式的散逸性. 结果表明, 两种θ-方法具有一致的散逸性特征,从而适合于求解此类散逸系统.向前型方程和滞后型方程的数值散逸性研究将是今后讨论的重点.

[1] Akhmet M U, Aruaslanc D, Ylmaz E. Stability in cellular neural networks with a piecewise constant argument[J]. J Comput Appl Math, 2010, 233(9):2365-2373.

[2] Gurcan F, Bozkurt F. Global stability in a population model with piecewise constant arguments[J]. J Math Anal Appl, 2009, 360(1)：334-342.

[3] Li Huaixing, Muroya Y, Nakata Y, et al. Global stability of nonautonomous logistic equations with a piecewise constant delay[J]. Nonlinear Analysis：Real World Applications, 2010, 11(3)：2115-2126.

[4] Xia Yonghui, Huang Zhengkun, Han Maoan. Existence of almost periodic solutions for forced perturbed systems with piecewise constant argument[J]. J Math Anal Appl, 2007, 333(2):798-816.

[5] Papaschinopoulos G, Stefanidou G, Efraimidis P. Existence, uniqueness and asymptotic behavior of the solutions of a fuzzy differential equation with piecewise constant argument[J]. Information Sciences, 2007, 177 (18)：3855-3870.

[6] Akhmet M U. On the reduction principle for differential equations with piecewise constant argument of generalized type[J]. J Math Anal Appl, 2007, 336(1)：646-663.

[7] Wiener J. Generalized solutions of functional differential equations[M]. Singapore：World Scientific, 1993：1-80.

[8] Liu Mingzhu, Song Minghui, Yang Zhanwen. Stability of Runge-Kutta methods in the numerical solution of equationu′(t)=au(t)+a0u([t])[J]. J Comput Appl Math, 2004, 166(2)：361-370.

[9] Song Minghui, Yang Zhanwen, Liu Mingzhu. Stability ofθ-methods for advanced differential equations with piecewise continuous arguments[J]. Comput Math Appl, 2005, 49(9/10)：1295-1301.

[10] Liu Mingzhu, Gao Jianfang, Yang Zhanwen. Oscillation analysis of numerical solution in theθ-methods for equationx′(t)+ax(t)+a1x([t-1])=0[J]. Appl Math Comput, 2007, 186(1)：566-578.

[11] Liu Mingzhu, Gao Jianfang, Yang Zhanwen. Preservation of oscillations of the Runge-Kutta method for equationx′(t)+ax(t)+a1x([t-1])=0[J]. Comput Math Appl, 2009, 58(6)：1113-1125.

[12] 文立平,余越昕,李寿佛. 一类求解分片延迟微分方程的线性多步法的散逸性[J]. 计算数学,2006, 28(1)：67-74.

[13] Wang Wansheng, Li Shoufu. Dissipativity of Runge-Kutta methods for neutral delay differential equations with piecewise constant delay[J]. Appl Math Lett, 2008, 21(9)：983-991.