素GPI-环中心闭包的本原性

游松发,曹明,冯怡君

(湖北大学数学与计算机科学学院,湖北 武汉 430062)

1 素环的中心闭包

当R是素环时,我们可断言Q也是素环.事实上,若0≠q∈Q,0≠p∈Q,有qQp=0,则∃0≠I1ΔR,0≠I2ΔR,有qI1⊆R且qI2⊆R,又q≠0,p≠0,∃a∈I1,b∈I2使qa≠0且pb≠0,因此(qa)R(pb)⊆qQpb=0,此与R的素性相矛盾.

我们还可断言Q的中心C是域.事实上,令0≠c∈C,选取R的非零理想I,使cI⊂R,因cI是R的非零理想.考虑d∶cI→R,使ca→a(∀a∈I),我们有d∈Q,且dca=a(∀a∈I),故dc=1,即C是域.

令S=RC,它是包含R的Q的一个子环,我们称C为R的广义形心,且称S为R的中心闭包,若1∈R,则C是S的中心,此时R的中心闭包为R的中心扩张.用证明Q是素环同样的方法可证S是素的.我们有

定理1令S=RC是素环R的中心闭包,对于a,b∈S,若∀x∈R,有axb=bxa,则a和b是C-相关的.

又f{(axy)r}=xbyr=f(xay)r,其中x,y∈I,r∈R,故f是R-模同态,即f∈F.

令q是Q中由f确定的元,p是Q中任一元,且对0≠WΔR有pW⊆R.对∀x,y∈I,w∈W,有

qp(wxay)=q{(pw)xay}=(pw)xby=p{wxby}=pq(wxay).

即(qp-pq)WJ=0.因此,qp=pq,即q∈C.特别地,对∀x,y∈I,我们有x(qa-b)y=qxay-xby=0,从而J(qa-b)J=0,据R的素性,我们有qa=b,即a,b是C-相关的.

(a)B≠0;

(b)S有一个极小右理想eS;

(c)eSe是C上有限维可除代数.

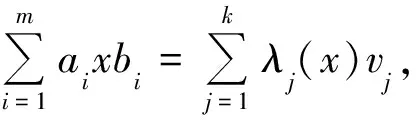
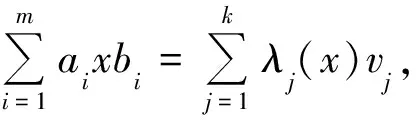
由归纳法,定理获证.

2 GPI-环及主要结果

令S=RC是素环R的中心闭包,C[x1,…,xn,…]是非交换未定元x1,…,xn,…的自由C-代数,我们构造C-代数S的C-泛积S,S中元具有形式f=∑βkai0xj1ai1…ain-1xjnain(βk∈C,aik∈S).若∃0≠f(x1,…,xn)∈S,对∀s1,…,sn∈S,有f(s1,…,sn)=0,则称S满足非平凡的广义多项式恒等式(C上),亦称S是GPI-环.称单项a0xi1a1xi2…an-1xinan(所有ai≠0)的次数为n,且称f(∈S)的次数为f的所有单项中最高次单项的次数.若S满足n次广义多项式恒等式,且n是最小的,我们可用多重线性化的程序[1]获得一个以x1,…,xn为未定元的非平凡的n次广义齐次多重线性恒等式：∑βiai0xj1ai1…ain-1xjnan=0,其中每一单项有固定的次数n,我们有下面的定理.

定理3若S=RC是素环R的中心闭包,则S是GPI-环,当且仅当S有一个极小右理想eS(因此S是本原的),且eSe是C上有限维可除代数,其中,e是S的幂等元.

定理3的证明(⟸)若dimCeSe

(⟹)若S满足j最小次数为n的非平凡广义多项式恒等式,不失一般性,可假设S满足n次齐次多重线性恒等式：

其中a1,…,am是S中C-无关的元,fi是n-1次非零的广义齐次多重线性多项式,g是f中x1不作为第一个变元的所有单项的和,再在g中把x1作为最后一个变元的所有单项(若存在)分离出来,得到

(1)

其中b1,…,bk是S中C-无关的元,gi是n-1次广义多项式,pi,qi是正整数次广义多项式.

(1)式右乘tb1(∀t∈S)得到

(2)

(1)式中用s1b1t(∀t∈S)代替x1得到

(3)

由(2)～(3)得到

(4)

若∀s2,…,sn,t∈S,有f1tb1-b1tf1=0,由定理1,有

f1(s2,…,sn)=λ(s2,…,sn)b,λ(s2,…,sn)∈C.

(5)

上述由恒等式(1)式推导到恒等式(4)式的过程中,某些单项可能消掉了,但单项中变元x1,…,xn的顺序并未改变,重复上述过程最多k次,我们可将(1)式变成形式

(6)

其中x1不作为g的所有单项的最后一个变元.

下面我们假设x1,x2,…,xr(r≤n)分别是最初恒等式中所有单项中的第一个变元,对{x1,x2,…,xr}(r≤n)中每一个变元,应用上述过程,经有限步,可由最初的恒等式得到恒等式

∑aix1fi+∑bix2gi+…+∑dixihi=0

(7)

其中{ai},{bi},…,{di}是S中C-无关的集,fi,gi,…,hi是非零的n-1次广义多项式,且x1不作为fi的所有单项的最后一个变元,x2不作为gi的所有单项的最后一个变元,…,xr不作为hi的所有单项的最后一个变元.

由于一定有变元作为最后一个变元出现在单项中,因而r

……

我们有n-1次恒等式

(8)

[1] Rowen L H. Polynomial identities in ring theory[M].New york:Academic Press,1980.

[2] Zheng yumei,You Songfa. A note on radicals in hypercentral extensions of rings[J]. SEA Bull Math,1993,17(1):105-108.

[3] 游松发.素GPI-环广义形心扩张的本原性[J].数学进展,2000,29(4):331-336.

[4] 游松发,郑玉美,胡幼刚.欧拉图与矩阵环的多项式恒等式[J].数学进展,2003,32(4):425-428.